Спросите Волшебника #229

Какую максимальную ставку вы бы порекомендовали казино, чтобы ограничить финансовый риск со стороны игроков с высокими ставками? Я знаю о математическом преимуществе казино в блэкджеке, но это не меняет того факта, что крупный игрок легко может нанести казино серьезный ущерб, если лимиты слишком высоки.

Frank от Copenhagen

Если бы я управлял казино, я бы применил критерий Келли для установления максимальных ставок. Я бы уравнял m*v/h для всех игр, где m — максимальная ставка, v — дисперсия, а h — преимущество казино. Назовем это коэффициентом риска. Например, предположим, что я готов поставить 150 000 долларов на ставку на Банкира в баккара , что примерно соответствует ставке крупного казино на Стрипе. Преимущество казино составляет 1,06%, а дисперсия — 0,93² ^. Таким образом, коэффициент риска равен 150 000 * 0,93² ^/ 0,0106 = 12 239 150.

Далее, давайте найдем m, чтобы уравнять коэффициент риска в блэкджеке. При либеральных правилах Strip преимущество казино составляет 0,29%. Допустим, игрок может сделать ставку до трех позиций. Стандартное отклонение на раздачу при трех ставках составляет 1,51957 , поэтому дисперсия равна ^1,51957² = 2,3091. Решая относительно m...

м × 2,3091 / 0,0029 = 12 239 150
м = 15 371 долл. США.

На практике мало кто из игроков идеально владеет базовой стратегией, поэтому я бы, возможно, увеличил сумму до 20 000 долларов. Примерно столько принимают крупные казино на Стрипе в блэкджеке, так что, думаю, здесь есть соразмерность. Более крупные ставки, на мой взгляд, следует принимать в играх-новинках.

Я участвовал в онлайн-покерной раздаче и хотел бы узнать вероятность такого исхода, пожалуйста:

David T. от Montego Bay

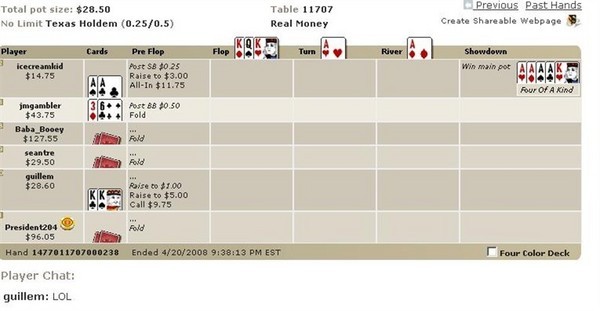
Обычно меня уже тошнит от вопросов на выбывание, но этот был слишком болезненным, чтобы его игнорировать. До раздачи первой карты вероятность того, что четыре короля будут побеждены четырьмя тузами в игре для двух игроков, у которых у обоих игроков есть карманные пары, составляет 2* комбинация (4,2)*комбинация(4,2)*44/(комбинация(52,2)*комбинация(50,2)*комбинация(48,5)) = 2*6*6*44/(1326*1225*1712304) = 1 из 877 961 175. Это была игра для шести игроков, поэтому комбинаций (6,2) = 15 различных пар игроков. В игре для шести игроков вероятность в 15 раз выше, или 1 из 58 530 745. После раздачи указанных карманных карт и до флопа вероятность того, что раздача завершится так, как это произошло, составляет 1 к 38 916.

Ваши стратегии игры в пай гоу (с использованием фишек) оптимизированы для правил казино Foxwoods , датированных февралем 1997 года. В некоторых из ваших стратегий, похоже, присутствует преимущество игрока или почти равные шансы. Знаете ли вы, читали ли какие-либо казино в Вегасе или где-либо еще ваш сайт и скорректировали ли они свои правила соответствующим образом? Есть ли у вас более актуальная информация о правилах казино в разных казино? Также, в вашей таблице шансов для пай гоу есть «оптимальная» стратегия, но мне не ясно, где находятся правила для этой стратегии. Что такое «оптимальная» стратегия? Мне очень нравится эта игра, и я ищу способы играть до конца, получать удовольствие и получать бонусы, не теряя слишком много денег.

анонимный

В Caesars Palace в Вегасе за последние несколько лет изменили правила игры. Раньше они никогда не делили пару «джи джун», а теперь делят. Недавно дилер в Mandalay Bay рассказал мне об изменении правил, согласно которым теперь играют 0-7 вместо 3-4. О причинах этих изменений я понятия не имею. Я был бы горд, если бы имел к этому какое-то отношение.

Недавно я добавил схему входа в казино Canberra . В будущем я, возможно, добавлю схемы входа в Claridge в Атлантик-Сити и Treasure Island в Лас-Вегасе. Преобразование их в HTML — утомительный и трудоемкий процесс, поэтому я еще этого не сделал.

Мой помощник Джей Би работает над оптимальной стратегией против системы казино Foxwoods. Она должна появиться на сайте в ближайшее время.

В игре в покер с одной картой используется колода из трех карт: туз, двойка и тройка. Туз — младшая карта, тройка — старшая. Каждый из двух игроков вносит по 1 доллару в банк. Затем каждый игрок получает по одной карте. Порядок ставок предопределен, первым ходит игрок 1. Игрок 1 может либо поставить 1 доллар, либо сделать чек. Если игрок 1 делает ставку, игрок 2 может либо ответить коллом, либо сбросить карты. Если игрок 1 делает чек, то игрок 2 может либо поставить 1 доллар, либо сделать чек. Если игрок 1 делает чек, и игрок 2 делает ставку, то игрок 1 может либо ответить коллом, либо сбросить карты. Если оба игрока делают чек или оба делают ставку, то банк выигрывает игрок с более старшей картой. Предполагая, что оба игрока — идеальные логики, какова оптимальная стратегия для каждого игрока?

Victor M. от Genoa City, WI

Надеюсь, вы довольны; я потратил на это весь день. Ответ и решение можно найти на моем другом сайте mathproblems.info , задача 203, или в научной статье Джейсона Свонсона «Теория игр и покер» .