Рулетка - Часто задаваемые вопросы
Как бы вы сыграли в рулетку вот так: поставили 5 долларов на 0 и 00, а 15 долларов — на два столбца? Разве у вас не было бы примерно 70% шансов на выигрыш?
У вас будет 2/38 шанс выиграть 140 долларов, 24/38 шанс выиграть 5 долларов и 12/38 шанс проиграть 40 долларов. Общая ожидаемая доходность составляет [(2/38)*140 + (24/38)*5 + (12/38)*-40]/40 = -5,26%. Преимущество казино такое же, как и на любой ставке в рулетке с двойным зеро (за исключением комбинации 0-00-1-2-3, которая составляет 7,89%).
Предположим, я захожу в казино и делаю ставку на два выигрыша в рулетке с коэффициентом 2 к 1, например, 100 долларов на 1-12 и 100 долларов на 13-24. В случае разовой ставки, разве мои шансы выиграть 100 долларов не составляют внушительные 63%? Я говорю не о долгосрочной перспективе, а только об одноразовой ставке.
Вы правы, шансы на выигрыш составляют 24/38, или около 63%. Однако, чтобы выиграть всего 100 долларов, нужно рискнуть 200 долларами. Если вы хотите еще больше увеличить свои шансы на выигрыш, сделайте ставку на любые 35 чисел. Вероятность выигрыша составит 92%.
Существует ли способ комбинировать ставки в рулетке, чтобы максимизировать свои шансы? Например, ставка на дюжину приносит выигрыш 2 к 1. Если я сделаю две ставки на дюжину, скажем, на первый и второй набор из 12 чисел, у меня будет 63,16% шансов на выигрыш. Это лучшие шансы, чем простая ставка на красное/черное, четное/нечетное или высокое/низкое. Хотя на самом деле я получаю выигрыш только 1 к 1, а не 2 к 1 (если выиграю, поскольку часть моей ставки должна проиграть, так как выигрышное число не может быть одновременно в первом и втором наборе из двенадцати чисел), шансы немного изменились в мою пользу за счет объединения двух ставок. Были ли определены шансы на подобные комбинации? Если да, то где я могу их найти?
Если вы избегаете комбинации 0-00-1-2-3, преимущество казино при любой комбинации ставок всегда составляет ровно 1/19, или 5,26%. Существуют способы увеличить вероятность выигрыша, но ценой уменьшения выигрыша относительно общей суммы ставки.
Вчера вечером я играл в рулетку, используя метод «Мартингейла»: дважды удваивал ставку после первого проигрыша. Глупо, конечно, но я обычно мало проигрываю и играю долго. В общем, игра закончилась для меня тем, что я ставил ровно, и за четыре броска трижды выпало число 9. Какова вероятность такого исхода? Звучит подозрительно? И вообще, когда-нибудь казино ловили на мошенничестве?
Вероятность выпадения любого числа три раза из 4 составляет 38*4*(1/38) 3 *(37/38) = 1/5932. Однако, если играть достаточно долго, то почти невозможно не заметить подобные необычные события. Это далеко не тот случай, когда это вызывает подозрения. Мошенничество в реальных казино действительно имеет место. Обычно это недобросовестный дилер, которого ловит служба безопасности казино. Были зафиксированы серьезные случаи мошенничества в онлайн-казино, но, насколько мне известно, ни один государственный орган никогда никого не осуждал.
Разве не хуже делать ставки на несколько чисел одновременно (как это делает большинство игроков), чем делать серию независимых ставок на одно число? Например, если у игрока есть 100 долларов, 10 ставок по 10 долларов на число «8» принесут меньший проигрыш, чем 10 ставок на 10 чисел за один спин? Мне кажется, что «хеджирование» просто гарантирует, что определенные ставки (в приведенном выше случае 9 ставок) ВСЕГДА будут проигрышными? Вы не затрагиваете тему «хеджирования» на своей странице?
См. мои Десять заповедей азартных игр . Шестая заповедь гласит: «никогда не делай ставки с хеджированием». Что касается вашего вопроса о рулетке, вероятность проиграть все десять ставок, делая по одной, составляет (37/38) ·10 = 76,59%. Вероятность проиграть все десять ставок, делая их все сразу на разные числа, составляет (28/38)·73,68%. Хеджирование, или ставки на десять чисел одновременно, снижает вероятность полного проигрыша, но также ограничивает максимальный выигрыш до 26 долларов. Игрок, делающий ставки по одному числу за раз, может выиграть до 350 долларов. Оба этих метода имеют одинаковую общую ожидаемую доходность в 94,74%.
Я прочитал вашу страницу о системах, и я рассказываю об этом людям уже много лет! Я работаю дилером в рулетке в казино и в разное время видел всевозможные системы. Я видел одну систему, которая, даже если в компьютерной симуляции она может не работать (вероятно, не будет работать), «кажется», что работает в реальной жизни. Это значит, что я видел, как она выигрывала чаще, чем проигрывала.
Суть в том, что игрок ставит 75 долларов на числа от 1 до 18, 50 долларов на третью двенадцатку и 10 долларов на пересечение чисел от 0 до 00, итого 135 долларов. Это покрывает все числа, кроме шести (от 19 до 22), и приносит 15 долларов выигрыша каждый раз, когда шарик не попадает в эти 6 чисел, ЗА ИСКЛЮЧЕНИЕМ случаев, когда выпадают 0 или 00, в этом случае выигрыш составляет 40 долларов. Я знаю, звучит безумно!!! Но поверьте, я видел, как эта система выигрывала чаще, чем проигрывала. Она также работает в обратном порядке (само собой разумеется). Мне бы очень хотелось узнать истинные шансы этой системы, но трудно сказать кому-то, что она не работает, когда он уходит от моего стола, разбогатев на 2 тысячи долларов :-)
Существует 30 способов выиграть 15 долларов, 6 способов проиграть 135 долларов и 2 способа выиграть 45 долларов (а не 40). Ожидаемая доходность этой комбинации ставок составляет ((30/38)*15 + (6/38)*-135 + (2/38)*(45))/135 = -0,0526, или 5,26%, что составляет преимущество казино по любой отдельной ставке или комбинации ставок, если удается избежать ужасной комбинации 0-00-1-2-3. В ваших наблюдениях, вероятно, было зафиксировано меньше ожидаемых 19-24 случаев, что объясняет иллюзию выигрышности этого метода.
Привет, Волшебник! Я вот думаю о рулетке. В программе Boss Media можно вращать колесо, не делая ставок. Разве это не в пользу игрока? В некоторых системах ставок на рулетку, например, в системе Мартингейла, вы удваиваете ставку при проигрыше и так далее. Разве нельзя просто наблюдать за колесом, не делая ставок, и делать ставку, основываясь на предыдущих вращениях? Например, можно вращать колесо 5 раз, прежде чем сделать ставку. Допустим, все числа нечетные. Разве не логичнее начать игру, сделав ставку на четные числа? Я понимаю, что это отчасти соответствует заблуждению игрока, и колесу все равно, какое было последнее вращение, но также вероятность того, что с каждым вращением будет выпадать нечетное число, уменьшается. Я на верном пути или просто повторяю старую теорию?
Вы просто повторяете ошибку игрока. Если шарик 100 раз подряд выпадал в категории «нечётное» на честном колесе, то вероятность того, что следующий спин будет чётным, всё равно остаётся такой же, как и при каждом последующем вращении, — 47,37% на колесе с двойным нулем. Так что то, что можно вращать колесо без ставок, не помогает. У шарика нет памяти.
Хотя рулетку, очевидно, нельзя обыграть случайно, я слышал, что её можно обыграть двумя способами, основанными на законах физики (в теории). Первый способ: высокотехнологичное устройство, измеряющее скорость шарика относительно скорости вращения колеса и предсказывающее сектор вылета с точностью около 40%. Второй способ: смещение колеса. Очевидно, что смещение колеса должно составлять не менее 5,26%, чтобы игрок оказался в выигрышном положении. Вопрос в том, сколько вращений, как вы скажете, Волшебник, нужно, чтобы определить смещение колеса, если оно вообще есть?
Я слышал об использовании обоих этих методов. Я мало что знаю об устройствах для подгонки колес, кроме того, что они, как известно, существуют и время от времени используются. Здесь, в Неваде, такое устройство было бы строго незаконным. О применении смещенных колес я слышу гораздо чаще. Это делалось много раз. Думаю, казино со старыми колесами — наиболее уязвимая цель. Я уже много лет говорю, что Аргентина — идеальная мишень для этого.
При игре по системе Мартингейла с удвоением ставки против рулетки с одним зеро на любой из равных вероятностей, я подсчитал, что проигрыш будет один раз из каждых 248 сессий. То есть, сессия, которая завершается либо выигрышем в одну единицу, либо проигрышем в 255 единиц. Правильно ли я рассчитал? Если нет, не могли бы вы указать правильные коэффициенты?
Если максимальный проигрыш составляет 255 единиц, то вы можете сделать до 8 ставок. Вероятность проигрыша восьми ставок подряд составляет (19/37) 8 = 0,004835. Таким образом, у вас есть 99,52% шансов выиграть одну единицу и 0,48% шансов проиграть 255 единиц.
В среднем, как часто повторяется число (например, две восьмерки подряд) в рулетке с одним нулем за 36 вращений?
Повторение можно ожидать примерно в 37 пар чисел. Таким образом, при 36 числах у нас получается 35 пар чисел. Следовательно, ожидаемое количество повторений составляет 35/37 = 0,9459.
Все говорят, что в долгосрочной перспективе рулетку невозможно обыграть с помощью математических систем. Но как объяснить тот факт, что есть профессиональные игроки, которые зарабатывают на жизнь рулеткой? Я думаю, это не просто хвастовство. На самом деле, в повседневной игре они выигрывают чаще, чем проигрывают.
Покажите мне человека, который выигрывает в честной игре в рулетку, и я покажу вам человека, которому просто повезло, и который, скорее всего, всё проиграет. Обыграть рулетку можно только умело, используя преимущества, например, используя смещенное колесо или «засекая время» вращения.
Я прочитал всё, что вы написали о рулетке, но ничего не нашёл о рулеточных игроках. Под пристальным взглядом менеджера рулеточного зала игрок подбрасывает «секцию», чтобы улучшить шансы казино. Игрок, который может подбрасывать зелёные карты, не всегда, но с хорошей вероятностью, может быть, один раз из 7 или 8, когда он хочет обыграть крупный прогрессивный джекпот.
Казино не нужно прибегать к подобным тактикам, чтобы выигрывать. Более того, казино нечего бояться игроков, использующих прогрессивный джекпот. В большинстве случаев выигрывают те, кто его использует, но те немногие, кто достиг лимита своего банкролла, выплачивают выигрыши всем победителям, а казино получает еще и дополнительную сумму. Кроме того, чтобы намеренно закрутить шар в определенную зону, потребуется немалое мастерство. Я не думаю, что это можно сделать с какой-либо заметной точностью.
Привет, Wizard! У тебя отличный сайт. В рулетке с двумя нулями я понимаю, что у всех ставок одинаково высокое преимущество казино, но я как раз заканчиваю курс статистики, и мне кажется, что не все ставки одинаковы из-за их стандартных отклонений. Например, ставка в 1 доллар на красное имеет стандартное отклонение 1,012019, в то время как ставка в 1 доллар на одно число имеет стандартное отклонение 5,839971, согласно моим расчетам. Таким образом, ожидаемая вероятность выигрыша за 1, 100 и 10000 испытаний составляет, соответственно, 0,4793, 0,3015 и 0,0000 для ставки с равными шансами и 0,4964, 0,4641 и 0,1837 для ставки на одно число. Правилен ли мой анализ? (Я предположил нормальное распределение). Спасибо!
Спасибо за комплимент. Во-первых, стандартное отклонение для любой ставки с равными шансами составляет 0,998614, а для ставки на одно число — 5,762617. Вероятность получить прибыль, делая ставки с равными шансами на 1, 100 и 10000 вращений, составляет 0,473684, 0,265023 и 0,00000007 соответственно. Вероятность получить прибыль, делая ставки на одно число на 1, 100 и 10000 вращений, составляет 0,0263158, 0,491567 и 0,18053280 соответственно. Похоже, вы пытаетесь доказать, что ставки на одно число лучше из-за более высокой вероятности получить прибыль по сравнению с несколькими ставками. Это правда, однако вероятность существенного проигрыша также намного выше. За игровую сессию ожидаемые результаты всегда располагаются где-то на колоколообразной кривой. При ставках с низкой волатильностью, таких как красное или черное, кривая распределения имеет острый угол и не сильно отклоняется от небольшого убытка. При ставках с высокой волатильностью, таких как отдельные числа, кривая распределения широкая, что позволяет получить гораздо более широкий диапазон чистых результатов, как хороших, так и плохих.
Мой коллега Д. утверждает, что он разработал идеальный способ стабильно выигрывать в рулетку. Я в этом не уверен. Ему просто везёт, или существует какая-то работающая система?
Ему просто повезло. Как я уже говорил тысячи раз, ни одна система ставок не выдержит испытания временем.
Я прочитал вашу тему о методе Мартингейла в рулетке. Я несколько раз пробовал этот метод на компьютере и выиграл 500 долларов. Потом пошел в казино и проиграл более 1000 долларов. Потому что черный выпал 8 раз подряд. Но я только начинаю изучать баккару. Я пробовал ее на компьютере и снова выиграл 500 долларов, делая ставки на банкира. Начинал с 20, потом дошел до 40, затем до 80 и так далее. Я выиграл 500 долларов, даже с учетом 5% комиссии за каждую раздачу. Как вы думаете, этот метод сработает в казино? Я решил спросить, прежде чем снова проиграю 1000 долларов. Как я уже сказал, черный выпал 8 раз подряд. Но как вы думаете, выиграет ли игрок 8 раз подряд? Плюс, эта игра хороша тем, что ничья – это пуш, тогда как в рулетке 0 или 00 – это проигрыш.
Мартингейл опасен в любой игре и в долгосрочной перспективе никогда не принесет выигрыша. Однако его лучше использовать в баккара, чем в рулетке, просто из-за меньшего преимущества казино. Вероятность выигрыша игрока 8 раз подряд составляет 0,493163^8 = 1 к 286. Также имейте в виду, что вы можете выиграть раздачу в конце серии и все равно остаться в проигрыше из-за комиссии. Например, если вы начали со ставки в 1 доллар и выиграли на 7-й раздаче, вы выиграете 60,80 долларов (64*95%), что не покроет 63 доллара предыдущих проигрышей.
Привет. Вы говорите, что все системы ставок обречены на провал. Если вы играете в рулетку и ставите одну единицу на числа от 1 до 12 и две единицы на числа от 13 до 24, разве у вас тогда не будет 66,66% шансов выйти в ноль или выиграть?
Не совсем. У вас будет 12/38 шанс выиграть 3 единицы, 12/38 — остаться в плюсе и 14/38 — проиграть 3 единицы. Ожидаемое значение равно [(12/38)*3 + (12/38)*0 + (14/38)*-3]/3 = (-6/38)/3 = -2/38 = -5,26%. Это будет справедливо для любой комбинации ставок, если вы избежите ужасной комбинации из 5 чисел (0/00/1/2/3). Если вы играете только один раз и хотите максимизировать вероятность выигрыша, сделайте ставки поровну на 35 чисел. У вас будет 92,11% шанс выиграть 1 единицу и 7,89% шанс проиграть 35 единиц.
Здравствуйте. Я уже несколько лет являюсь заядлым игроком в рулетку, и впервые в жизни подумываю попробовать систему для игры в рулетку… Я понимаю ваше отношение к этим так называемым «системам» и мошенникам, стоящим за ними, и поверьте, я чувствую то же самое, но я наткнулся на две системы, которые нельзя игнорировать…
Первая стратегия — это 3q/A, описанная в книге Р. Д. Эллисона «Gamble to win: Roulette», подтвержденный процент выигрыша которой составляет 7,94% (7500 вращений). Система была протестирована и разработана совместно с книгами «Spin roulette Gold» Фрэнка Скоблета и «Roulette system tester» Эрика Сент-Жермена.
Вторая система — это система игры в рулетку Дона Янга, которая, согласно подтвержденным данным, превосходит тест системы игры в рулетку от Zumma Publishing (15000 вращений).
Честно говоря, я всё ещё немного скептически отношусь к трате денег на эти системы, но поскольку они доказали свою эффективность в долгосрочной перспективе, я не вижу причин, почему бы мне не стоит этого делать. В конце концов, прохождение этих тестов должно что-то значить...
Каково ваше мнение об этих системах? И стоит ли мне их попробовать?
Большое спасибо! Хорошего дня! С наилучшими пожеланиями!
7500 вращений? И это всё? Любой может показать прибыль в 7,94% от общей суммы ставок за 7500 вращений, если будет делать агрессивные ставки. То же самое верно и для 15000 вращений. Большинство систем рассчитаны на большое количество мелких выигрышей и небольшое количество крупных проигрышей. Система, требующая огромного банкролла, легко может показать прибыль за 15000 вращений. В конце концов, проигрыши придут, и система не выдержит испытания временем. Крупные проигрыши могут также прийти в начале. Настоящий способ проверить систему — это сыграть с ней миллиарды раз. Моё мнение об этих системах такое же, как и обо всех системах: они бесполезны. У меня нет проблем с тем, чтобы вы их пробовали, но у меня есть проблема с тем, чтобы кто-то вкладывал хоть копейку в карманы тех, кто их продаёт.
Примечание: См. продолжение этого вопроса в следующей колонке .
Уважаемый господин! В игре в рулетку с одним зеро ВЕРОЯТНОСТЬ выигрыша увеличивается, если вы ставите часть своих денег на меньшее количество чисел в течение большего количества вращений, а не на большее количество чисел за одно вращение. Например: если вы готовы рискнуть 500 долларами, чтобы выиграть 250 долларов, то вы можете: Вариант (А): поставить 250 долларов на любое из двух десятков, и если вы выиграете, то получите 250 долларов. Вероятность этого события составляет 24/37 = (0,648648). Вариант (Б): поставить 125 на любой один десяток, и если вы выиграете, то получите 250 долларов и сможете уйти. Однако, если вы проиграете, вы можете поставить 187,5 долларов на тот же десяток, и если вы выиграете, то получите 375 долларов, что вернет вам 250 долларов и 125 долларов, которые вы проиграли в предыдущем вращении. Если вы проиграете на обоих вращениях, у вас все равно останется 187,5$, и вы можете поставить 20,833333$ на любые девять чисел. В случае выигрыша вы получите 750$, что равно вашему первоначальному капиталу в 500$ плюс 250$ выигрыша, что и было вашей целью. Вероятность этого события, то есть совпадения хотя бы дюжины или девяти чисел хотя бы раз за три вращения, равна [1-(25/37)x(25/37)x(28/37)]=0,65451. Следовательно, при том же капитале и том же выигрыше вы можете увеличить свою ВЕРОЯТНОСТЬ успеха, как в варианте (B), если будете играть на меньшем количестве чисел с меньшими деньгами, но, ВОЗМОЖНО, на большем количестве вращений (так как вы можете выиграть на первом вращении). Вы даже можете еще больше повысить свою вероятность, если будете играть только на шести числах за раз и попытаетесь выиграть 250$. Есть какие-нибудь объяснения??!!!! Заверяю Вас в своем высочайшем уважении и с нетерпением жду Вашего благосклонного ответа.
Вы правы, что вариант B имеет большую вероятность успеха, хотя цель и капитал одинаковы. Причина в том, что средняя сумма ставки в варианте B меньше, следовательно, ваши деньги меньше подвержены влиянию преимущества казино, поэтому вероятность выигрыша увеличивается. Сумма ставки в варианте A всегда составляет 500 долларов. Средняя сумма ставки в варианте B составляет (12/37)*125 + (25/37)*(12/37)*(125+187.5)+ (25/37)*(25/37)*(125+187.5+187.5) = 337.29.
Когда я участвовал в Vegas Challenge, за несколько минут до конца у меня было около 8000 долларов, и мне нужно было набрать хотя бы 24 000. Поэтому я разделил свой банкролл на четыре части по 2000 долларов и поставил на каждую комбинацию из 4 чисел, каждая из которых принесла бы 22 000 долларов. Таким образом, я не подвергал всю свою ставку влиянию казино, что увеличило мои шансы на выигрыш.
Ставка на все 38 чисел в рулетке сделала бы невозможным обыграть шансы даже на короткое время, а при ставке в 1 доллар на каждое число потери за каждый бросок колеса составили бы 2 доллара (колесо 0, 00, без выгодных правил для ставок с равными шансами). Кажется ли разумным, что должен существовать оптимальный диапазон чисел для ставок, основанный на статистике?
Я оцениваю ценность ставки по ожидаемой прибыли, а не по вероятности выигрыша. Таким образом, ставка на все 38 чисел имеет преимущество казино в 2/38 = 5,26%, как и при ставке на одно число или любое количество чисел. Хотя вероятность чистого выигрыша при ставке на все 38 чисел равна 0%, минусом является потеря всего 5,26% от общей суммы ставок. Если вы вынуждены делать ставки и хотите минимизировать дисперсию, то вам следует ставить на все 38 чисел. Практический пример: если у вас есть рекламные фишки, которые вы должны поставить, и вы не хотите рисковать, чтобы получить от них точную ожидаемую прибыль. Таким образом, отвечая на ваш вопрос, оптимального диапазона чисел не существует. Все диапазоны имеют одинаковую ожидаемую прибыль.
Сегодня вышла история о британце, который поставил все свои сбережения на один бросок рулетки. Мы с другом спорим о том, какая ставка в казино является лучшей для такого рода пари. Если можно сделать только одну ставку и вы хотите максимизировать свои шансы, в какую игру лучше всего играть и какая ставка будет оптимальной?
Во-первых, позвольте мне сказать, что этот парень был дураком. Он поставил 138 000 долларов на обычное американское колесо рулетки с двумя нулями и преимуществом казино в 5,26%. Это составило ожидаемый убыток в 7263 доллара. Однако, если бы он проехал 10 минут до Белладжио, Миража или Аладдина, он мог бы сделать ставку на колесо с одним нулем, которое следует европейскому правилу, согласно которому половина ставки с равными шансами возвращается, если шарик попадает в ноль. Он в любом случае планировал сделать ставку с равными шансами. Таким образом, на этих колесах с полными европейскими правилами его преимущество казино составило бы всего 1,35%, а ожидаемый убыток — всего 1865 долларов.
Отвечая на ваш вопрос, если бы меня заставили сделать только одну ставку с равными шансами, я бы выбрал ставку на банкира в баккара с преимуществом казино в 1,06%.
Каков мой риск разорения при следующей схеме ставок в рулетке?
Вопросы, связанные с риском разорения, математически сложны. Если это не простая игра на победу/поражение, я бы рекомендовал провести случайное моделирование на компьютере.
Я живу в Нью-Джерси, примерно в двух часах езды к северу от Атлантик-Сити. Не могли бы вы подсказать, где находится ближайшая к моему региону европейская рулетка?
В Атлантик-Сити много казино с одним нулем. В большинстве казино они есть, но минимальная ставка составляет 25 долларов.
Я был в онлайн-казино. Играл в рулетку. Делал безопасные ставки, только на 1-ю двойку (L), 2-ю двойку (M) и 3-ю двойку (H). Пять раз вращал колесо, не делая ставок, ожидая, что одна из комбинаций чисел не выпадет, чтобы я мог поставить на неё, надеясь, что это изменит вероятность её выпадения в мою пользу. Пять вращений спустя L не выпал. Я продолжал ставить на L, полагая, что числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 или 12 выпадут в течение 12 вращений, чтобы я хотя бы смог вернуть свои деньги... но этого не произошло. Стол вращался 17 раз подряд без выпадения МАЛОГО числа, и я потерял 258 долларов, потеряв все деньги... это были бонусные деньги. Это вопрос из трёх частей:
- Действительно ли ожидание пяти вращений без выпадения низкого числа увеличило вероятность появления буквы L?
- Какова вероятность того, что низкое число не будет встречаться 16 раз подряд?
- Какова вероятность того, что низкое число не выпадет 17 раз подряд?
Спасибо, я также хочу поблагодарить вас за это руководство по игре в блэкджек, я превратил 5 долларов в 100 долларов, используя ваш метод.
- Нет
- В онлайн-казино используется колесо с одним нулем. Таким образом, вероятность того, что 16 раз выпадет ноль, составляет (25/37) 16 = 0,1887%.
- (25/37) 17 = 0,1275%.
Каковы шансы дилера получить 5 одинаковых чисел за 10 вращений рулетки?
Вероятность того, что любое число выпадет ровно 5 раз из 10 вращений в рулетке с двумя нулями, можно приблизительно оценить как 38* комбинация (10,5)*(1/38) 5 *(37/38) 5 = 1 из 359275.
Поздравляю с отличным сайтом! Я прекрасно понимаю ваше недовольство распространением выплат в блэкджеке 6 к 5, но мне очень любопытно, почему американцы, кажется, без всяких возражений принимают рулетку с нулевым балансом. Эта рулетка почти преступна и должна стоять в одном ряду с кено и игровыми автоматами.
Спасибо. Вы правы. Преимущество казино в блэкджеке 6 к 5 составляет 1,44% по обычным правилам, в то время как в рулетке с двойным зеро — 5,26%. Это в 3,7 раза хуже. Однако за годы работы я понял, что практически невозможно заставить игроков покинуть игру, которая им нравится, независимо от того, насколько велико преимущество казино. Поэтому лучшее, что я могу сделать, это посоветовать им, как играть в выбранную ими игру. Для игроков в блэкджек по-прежнему существует множество игр 3 к 2. Игра в 6 к 5 дает казино дополнительное преимущество в 0,8% без всякой причины. Я также подчеркиваю важность поиска рулетки с одним зеро, если вы играете в рулетку. Так что я не вижу противоречия.
Пожалуйста, объясните мне, как работают лимиты ставок в рулетке и в чем разница между минимальным лимитом для отдельного числа и лимитом для всего стола. Если возможно, приведите примеры.
В рулетке обычно есть два минимальных порога. Например: 5 долларов на внешние ставки, 1 доллар на внутренние. Внешние ставки — это все ставки с равными шансами, ставки на столбцы и ставки на дюжины. Внутренние ставки — это ставки на числа, включая группы из 2, 3, 4, 5 и 6. В этом случае минимальный порог для внешних ставок составляет 5 долларов, а для внутренних — 1 доллар. Однако вы должны поставить в общей сложности не менее 5 долларов на внутренние ставки или не делать ни одной ставки вообще.
Я работаю в казино, и у нас есть пари, что дилер рулетки не может повлиять на исход броска. Конечно, есть и те, кто считает, что это возможно. Не на какое-то число, конечно, а, возможно, на часть колеса. Какой тест вы бы сочли хорошим для разумного определения того, повлиял ли дилер на результаты? Если количество попыток будет достаточным, я с удовольствием поделюсь результатами.
Я на вашей стороне. Если бы это было возможно, дилеры могли бы легко вступать в сговор с игроками и делить прибыль. Однако я никогда не слышу о подобных случаях. Хорошим тестом было бы попросить человека, утверждающего, что он может влиять на бросок колеса, попытаться выбить нужный результат в определенной половине колеса как можно больше раз за 100 вращений. Чем больше раз ему это удастся, тем больше веса будет иметь его утверждение. В таблице ниже показана вероятность от 50 до 70 успешных вращений. Например, вероятность 60 или более успешных вращений составляет 2,8444%. В статистике обычно используются пороговые значения достоверности 90%, 95% и 99%. Чтобы пройти тест на 90% достоверности, в котором вероятность неудачи при случайных вращениях составляет 90%, количество успешных вращений должно быть 57 или более. Чтобы пройти тест на 95% достоверности, это число должно быть 59 или более, а на 99% — 63 или более.
Вероятность как минимум 50-70 успешных вращений рулетки
| Победы | Вероятность |
| 70 | 0.000039 |
| 69 | 0.000092 |
| 68 | 0.000204 |
| 67 | 0.000437 |
| 66 | 0.000895 |
| 65 | 0.001759 |
| 64 | 0.003319 |
| 63 | 0.006016 |
| 62 | 0.010489 |
| 61 | 0,0176 |
| 60 | 0.028444 |
| 59 | 0.044313 |
| 58 | 0.066605 |
| 57 | 0.096674 |
| 56 | 0.135627 |
| 55 | 0.184101 |
| 54 | 0.242059 |
| 53 | 0.30865 |
| 52 | 0.382177 |
| 51 | 0.460205 |
| 50 | 0.539795 |
На сайте www.ccc-casino.com нет рулетки с нулевым значением, которую они называют «Супершансная рулетка». Существуют ли какие-либо системы, которые были бы эффективны, если бы не было нуля? Можно ли без нуля эффективно играть одновременно и в чёрное, и в красное, поскольку нет страха перед нулём?
Я пытался найти эту игру, но сайт был недоступен, когда я проверял. Однако, если предположить, что такая игра существует, ответ — нет. В долгосрочной перспективе ни одна система не сможет её победить или проиграть ей. Ожидаемая ценность любой системы будет равна нулю.
Рулетка с одним нулем. Какова вероятность того, что любое число (от 0 до 36) выпадет более одного раза в трех последовательных вращениях? Спасибо за ваше время!
Независимо от того, какое число выпало первым, вероятность того, что совпадет только второе вращение, составляет (1/37)*(36/37). Вероятность того, что совпадет только третье вращение, составляет (36/37)*(1/37). Вероятность того, что не совпадут ни одно вращение, но совпадут второе и третье, составляет (36/37)*(1/37). Вероятность того, что совпадут и второе, и третье вращения, составляет (1/37)*(1/37). Сложив все это, получаем 3*(1/37)*(36/37)+ (1/37)*(1/37) = 7,962%.
Думаю, вас это может заинтересовать. Я пользуюсь Betfair здесь, в Великобритании. Уверен, вам, хорошим людям в Америке, по какой-то причине не разрешают им пользоваться, но если вы с ним не знакомы, зайдите на betfair.co.uk и посмотрите. Это биржа ставок, а не букмекерская контора. В общем, мой вопрос вот в чём. Теперь они предлагают рулетку БЕЗ НОЛЬ, да, без нуля. Это действительно так. Можете ли вы предложить хорошую стратегию, которую можно было бы использовать, и если да, то стоит ли держать её в секрете? С наилучшими пожеланиями, Джонатан. P.S. Они также предлагают другие игры казино без преимущества казино.
Я попытался зарегистрироваться там, чтобы проверить это, но они блокируют игроков из США. Мне сказали, что минимальная ставка составляет 2 фунта стерлингов, а максимальная — 50 фунтов стерлингов. Даже в игре с нулевым преимуществом казино, такой как рулетка без нуля, нет системы ставок, которая бы позволила подняться выше или опуститься ниже отметки в 0%. Что бы вы ни делали, чем больше вы это делаете, тем ближе фактический выигрыш казино будет к 0%.
Вы говорите, что в рулетке нет выигрышной системы. Гонсало Гарсиа-Пелайо и его семья выиграли много денег во многих казино по всему миру. Они даже опубликовали книгу, в которой описали, как им это удалось. Каково ваше мнение?
Я как-то видел телепередачу о нём, и я восхищаюсь тем, что он сделал. Под «системой» я подразумеваю схему ставок, например, Мартингейл , применённую к игре с преимуществом казино, такой как честная рулетка. Гонсало Гарсиа-Пелайо успешно проводил анализ того, как часто шарик попадал в каждое число, пытаясь найти и затем использовать неравномерность вращения рулетки. Это я бы назвал стратегией, а не системой. Существует множество прибыльных стратегий для победы над казино, но нет ни одной прибыльной системы ставок.
Если я покажу вам игру в рулетку без нулей, где действуют все обычные правила рулетки, возможно ли выиграть в 100% случаев?
Нет.
Я давний подписчик вашей рассылки и по-прежнему в восторге от вашего сайта. Я наткнулся на сайт казино, предлагающий рулетку, в которой колесо не содержит нулей. На нем только числа от 1 до 36, и действуют все стандартные правила рулетки. Видите ли вы какой-нибудь способ воспользоваться этим? Я знаю, что вам не нравятся системы ставок, но в данном случае нет преимущества казино. Должна существовать система управления капиталом, которая могла бы прибыльно работать с такими лимитами стола. Любые советы приветствуются.
Спасибо за добрые слова. Кажется, я уже отвечал на этот вопрос, но нет, даже при нулевом преимуществе казино нет такой системы ставок, которая могла бы приносить прибыль в долгосрочной перспективе.
Здравствуйте, по понятным причинам я был бы признателен, если бы вы никому не рассказывали мое имя. В казино, где я работаю, среди дилеров рулетки практически единодушно считают, что они могут «контролировать вращение» и с легкостью попадать по определенным участкам колеса или намеренно пропускать другие. Учитывая все факторы, влияющие на вращение шарика в рулетке, включая выступы (бугорки) по бокам, направление движения шарика и скорость вращения колеса и т. д., — как вы думаете, есть ли в этом что-то правдивое? Достаточно ли этого, чтобы нечестный дилер помог игроку преодолеть огромное преимущество казино?
Это далеко не первый раз, когда я слышу подобное утверждение, и я отношусь к нему очень скептически. Большинство дилеров также верят в мифы, например, что плохой игрок на третьей базе заставит других игроков проиграть в блэкджеке, поэтому в целом они не самые скептически настроенные. Мне кажется, дело в том, что они помнят те случаи, когда им удавалось контролировать вращение карты, и удобно забывают те, когда это не удавалось. Точно так же, как они помнят, когда игрок на третьей базе забирал у дилера карту, которая привела к перебору, но забывают те случаи, когда он спасал стол.
Если бы дилеры действительно могли так делать, было бы легко организовать подставную игру, которая принесла бы ему победу, а другим игрокам – поражение, чтобы компенсировать проигрыш. Пока они соблюдали все правила игры и не появлялись с подставным лицом на публике, всё выглядело бы совершенно законно. Однако о таких случаях никогда не говорят. Можно предположить, что сторонники таких систем утверждают, что те просто действуют незаметно, но так говорят и сторонники бесполезных систем ставок. Если бы это было так просто, как утверждают дилеры рулетки на вашей работе, проблема мошенничества была бы повсеместной.
В рулетке с двумя нулями, какова вероятность того, что ни одно число не выпадет к 200-му вращению?
Вероятность того, что какое-либо заданное число не выпадет, составляет (37/38) 200 = 0,48%.
Имея 38 чисел, мы могли бы ошибочно сказать, что вероятность того, что хотя бы одно из них не будет поражено, составляет 38 × (37/38) 200 = 18,34%.
Причина неверности в том, что дважды учитывается случай, когда два числа не выпадают. Поэтому нам нужно вычесть эти вероятности. Из 38 комбинаций (38,2) = 703, состоящих из двух чисел. Вероятность того, что никакие два заданных числа не выпадут, равна (36/38) ²⁰⁰ = 0,000020127. Нам нужно вычесть вероятность того, что оба числа не выпадут. Таким образом, мы получаем:
38×(37/38) 200 – объединить(38,2)×(36/38) 200 = 16,9255%.
Однако теперь мы исключили вероятность того, что три числа не совпадут. Для любой заданной группы из трех чисел мы трижды подсчитали вероятность того, что хотя бы одно число не совпадет. Затем мы трижды вычли вероятность того, что из трех чисел выпадут два, в результате чего вероятность того, что не совпадут все три числа, осталась равной нулю. Существует комбинаций (38,3) = 8436 таких групп. Добавив их обратно, мы получаем:
38×(37/38) 200 – комбинация(38,2)×(36/38) 200 + комбинация(38,3)×(35/38) 200 = 16,9862%.
Однако теперь мы переоценили вероятность того, что четыре числа не совпадут. Для каждой из комбинаций (38,4) = 73 815 групп по четыре числа каждая изначально была подсчитана четыре раза. Затем мы вычли каждую из комбинаций (4,2) = 6 групп по 2 из 4. Затем мы добавили обратно 4 группы по 3 из 4. Таким образом, для каждого объединения четырех чисел оно было подсчитано 4 − 6 + 4 = 2 раза. Чтобы скорректировать двойной подсчет, мы должны вычесть для каждой группы. Вычитая их, мы теперь получаем:
38×(37/38) 200 – комбинация(38,2)×(36/38) 200 + комбинация(38,3)×(35/38) 200 – комбинация(38,4)×(34/38) 200 = 16,9845%.
Продолжая этот процесс, мы будем поочередно складывать и вычитать, пока не пропустим 37 чисел. Таким образом, вероятность того, что хотя бы одно число никогда не будет найдено, составляет:
Сумма i=1 до 37 [(-1) (i+1) × combin(38,i) × ((38-i)/38) 38 ] = 16.9845715651245%
Вот результаты случайного моделирования 126 900 000 подобных экспериментов с 200 вращениями.
Выпавшие числа за 200 вращений рулетки
| Цифры достигли цели | Наблюдения | Соотношение |
|---|---|---|
| 31 или меньше | 0 | 0 |
| 32 | 1 | 0.00000001 |
| 33 | 33 | 0.00000026 |
| 34 | 1812 | 0.00001428 |
| 35 | 68845 | 0.00054251 |
| 36 | 1577029 | 0.01242734 |
| 37 | 19904109 | 0.15684877 |
| 38 | 105348171 | 0.83016683 |
| Общий | 126900000 | 1 |
Доля случаев, когда хотя бы одно число не совпало с прогнозом, составила 0,169833.
У меня есть друг, который работал в казино и следил за рулеточными столами, и он рассказывал мне, что когда люди начинают выигрывать, казино меняет крупье. Я также видел, как один из сотрудников просил крупье вращать колесо рулетки с другой скоростью. Разве это не означает, что казино уверены в том, что крупье может вызвать неслучайную последовательность чисел? Разве это не означает, что игрок может искать «счастливый» стол, где крупные игроки, вращающие колесо обычным способом, дают ему больше шансов на выигрыш?
К сожалению, невежество может зайти довольно высоко по лестнице. Я не оспариваю, что эксперт может засечь время вращения колеса даже на очень низкой скорости. Однако, если отбросить этот вопрос, смена дилера не меняет шансов. Не существует такого понятия, как удачливый или неудачливый дилер. От суеверий трудно избавиться. Как я уже много раз говорил, чем нелепее убеждение, тем упорнее его придерживаются.
Уважаемый господин, я "зафиксировал" автоматическую игру в рулетку с одним зеро на 8672 игры. Мое заранее определенное число выпало невероятные 278 раз. Я выбрал это число из-за износа ячеек. Насколько я уверен, что вероятность выпадения этого числа выше, чем 1/37?
Если моя терминология верна, «угадывание положения шара» означает предсказание места приземления шарика на основе его скорости, местоположения и скорости вращения колеса. Похоже, вы используете смещенное колесо, что является другим способом получения преимущества. Раз уж мы заговорили об этом, третий способ получения преимущества — это использование «подписи дилера», когда крупье настолько стабилен, что скорость шара и колеса практически одинакова при каждом вращении. Это позволяет игроку предсказывать место приземления шарика на основе его местоположения и прошлых результатов.
Отвечая на ваш вопрос, ожидаемое количество попаданий по вашему числу составляет 8672/37 = 234,38. Дисперсия равна 8672 × (1/37) × (36/37) = 228,04. Стандартное отклонение равно квадратному корню из дисперсии, или 15,10. У вас было на 278 - 234,38 = 43,62 попаданий больше, чем ожидалось. Это (43,62 - 0,5) / 15,10 = 2,8556 стандартных отклонений. Причина вычитания 0,5 трудно объяснить. Достаточно сказать, что это поправочный коэффициент для использования непрерывной функции для оценки дискретной функции. Применяя гауссову аппроксимацию, вероятность попадания по вашему числу столько раз или больше составляет 0,21%. Таким образом, есть большая вероятность, что вы нашли смещенное колесо. Однако всё ещё существует вероятность 1 к 466, что это была просто удача.
Известна история о соревновании по «замораживанию» ставок между японским хайроллером Кашиваги и Дональдом Трампом, которое состоялось 20 лет назад. Кашиваги не разрешалось ставить более 200 000 долларов за раздачу в баккара. Игра заканчивалась, когда либо казино, либо игрок опережали соперника на 12 миллионов долларов. Предположим, что Кашиваги всегда ставил максимальную ставку на Банкира. Какова вероятность победы Кашиваги?
Математические вычисления проще, если он сделал ставку на Игрока. Я решаю аналогичную задачу по рулетке на своем сайте mathproblems.info, задача номер 116. Для ставок с равными шансами общая формула выглядит так: ((q/p) b -1)/((q/p) g -1), где:
b = начальный баланс в единицах.
g = целевой объем денежных средств в единицах.
p = вероятность выигрыша в любой конкретной ставке, без учета ничьих.
q = вероятность проигрыша в любой конкретной ставке, без учета ничьих.
В данном случае игрок начинает с 12 миллионов долларов, или 60 единиц по 200 000 долларов, и будет играть до тех пор, пока не наберет 120 единиц или не проиграет. Таким образом, в случае ставки игрока значения формулы следующие:
b = 60
g = 120
p = 0,493175
q = 0,506825
Таким образом, ответ равен ((0,506825/0,493175) 60 -1)/(( 0,506825/0,493175) 120 -1) = 16,27%.
Ставка на Банкира значительно усложняется из-за 5% комиссии. Это создает реальную вероятность того, что игрок превысит свою цель. Если добавить правило, согласно которому, если выигрышная ставка приведет игрока к достижению цели, он может поставить только ту сумму, которая необходима для достижения ровно 12 миллионов долларов, то я оцениваю вероятность его успеха в 21,66%.
Более простая формула для вероятности удвоения банкролла: 1/[1+(q/p) b].
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В среднем, сколько попыток потребуется в рулетке с 38 числами, прежде чем какое-либо число повторится?
С учетом первого испытания, я показываю, что среднее значение равно 8,408797, медиана равна 8, а мода равна 7.
Вероятность того, что два числа не повторяются, составляет 37/38 = 97,37%.
Вероятность выпадения трех чисел без повторения составляет (37/38)×(36/38) = 92,24%.
Вероятность того, что четыре числа не повторятся, составляет (37/38)×(36/38)×(35/38) = 84,96%.
Следуя этой схеме, вероятность отсутствия повторений в 8 числах составляет (37/38)×(36/38)×(35/38)×...×(31/38) = 45,35%.
Таким образом, вероятность повторения в пределах 8 чисел составляет 100% - 45,35% = 54,65%.
Я подозреваю, что большинство людей оценили бы вероятность повторения числа в пределах 8 цифр как меньшую. Если вы не прочь воспользоваться неуверенностью ваших друзей в математике, предложите пари, что для повторения хотя бы одного числа потребуется 8 или меньше цифр. То есть вы ставите на 8 или меньше, а ваш друг — на 9 или больше. Если он/она откажется, предложите поставить на 7 или больше, что даст 55,59% шансов на выигрыш. В общем, победит та сторона, которая покроет медиану в 8 цифр.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В программе "Hustling the House" на канале Discovery Channel был длинный сюжет о лучшем способе превратить 30 долларов в 1000. В нем Энди Блох сказал: "Если у вас в кармане 30 долларов, и вы хотите превратить их в 1000, то рулетка — ваша единственная игра". Энди продолжил объяснять, почему ставка в 30 долларов на одно число лучше, чем пять экспрессов ставок с равными шансами.
Прав ли Энди, утверждая, что лучший способ превратить 30 долларов в 1000 — это поставить все 30 долларов на одно число в рулетке?
Нет, он не прав. Вероятность выигрыша по стратегии одиночной ставки Энди составляет 1/38 = 2,6316%.
После многочисленных проб и ошибок я разработал свою стратегию игры в рулетку "На удачу", которая увеличивает шансы превратить 30 долларов в 1000 долларов до 2,8074%.
Стратегия «Аве Мария» волшебника в рулетке:
Данная стратегия предполагает, что ставки должны быть сделаны с шагом в 1 доллар. При всех расчетах ставок округляйте сумму в меньшую сторону.
Позволять:
b = Ваш банкролл
g = Ваша цель
- Если 2*b >=g, то сделайте ставку (gb) на любую ставку с равными шансами.
- В противном случае, если 3*b >=g, то ставьте (gb)/2 на любой столбец.
- В противном случае, если 6*b >=g, то ставьте (gb)/5 на любые шесть линий (шесть чисел).
- В противном случае, если 9*b >=g, то ставьте (gb)/8 на любой угол (четыре числа).
- В противном случае, если 12*b >=g, то ставьте (gb)/11 на любую улицу (три числа).
- В противном случае, если 18*b >=g, то ставьте (gb)/17 на любое расщепление (два числа).
- В противном случае, сделайте ставку (gb)/35 на любой отдельный номер.
Другими словами, всегда старайтесь достичь цели, сделав всего одну ставку, если это возможно, не превышая её. Если есть несколько способов это сделать, выбирайте тот, у которого наибольшая вероятность выигрыша.
А как насчет других игр, спросите вы? По словам диктора канала Discovery, «все согласны с тем, что рулетка — лучший способ быстро разбогатеть в казино». Что ж, я так не считаю. Даже если ограничиться распространенными играми и правилами, я считаю, что крэпс лучше. В частности, ставки на то, что «не пройдет» или «против», и ставки на шансы.
Следуя моей стратегии «Hail Mary» для игры в крэпс (описанной ниже), вероятность превратить 30 долларов в 1000 составляет 2,9244%. Это предполагает, что игрок может поставить на ставку с коэффициентом 6x, независимо от точки (что имеет место, когда разрешены коэффициенты 3x, 4x и 5x). Эта вероятность успеха на 0,117% выше, чем при использовании моей стратегии «Hail Mary» для рулетки, и на 0,2928% выше, чем при использовании стратегии Энди Блоха.
Энди мог бы возразить, что мой аргумент выше основан на предположении о минимальной ставке в 1 доллар, что трудно найти в Вегасе в игре с живым дилером. Предвидя такое предположение, я провел анализ обеих игр, исходя из предположения о минимальной ставке в 5 долларов и ставках с шагом в 5 долларов. В этом случае вероятность успеха при использовании моей стратегии «Hail Mary» составляет 2,753% в рулетке и 2,891% в крэпсе. В обоих случаях это больше, чем 2,632% при использовании стратегии Энди Блоха.
Честно говоря, телеканал Discovery Channel никогда бы не показал в эфире эту безумную тираду и наверняка искал что-то простое, понятное широкой публике. Энди, безусловно, давал им то, что они хотели услышать. Основная идея его совета заключается в том, что если вы хотите достичь определенной цели, то стратегия «быстрого удара и отступления» гораздо лучше, чем позволить преимуществу казино измотать вас многочисленными ставками. Это определенно правда, и я проповедую это уже 17 лет.
Стратегия «Аве Мария» волшебника в игре в кости.
Эта стратегия предполагает, что ставки должны быть сделаны с шагом в 1 доллар, а выигрыши будут округляться до ближайшего доллара в меньшую сторону. При расчете ставок никогда не ставьте столько, чтобы превысить целевой показатель. Также никогда не делайте ставку, которая приведет к округлению суммы в меньшую сторону.
Позволять:
b = Ваш банкролл
g = Ваша цель
- Ставьте max($1,min(b/7,(gb)/6)) на то, что не пройдете.
- Если выпало очко, и у вас достаточно средств для ставки с полным коэффициентом, то сделайте ставку против с полным коэффициентом. В противном случае, сделайте ставку против любой суммы, которую сможете.
Надеюсь, Энди и телеканал Discovery довольны. Я потратил несколько дней на моделирование, чтобы доказать им обратное.
Этот вопрос был поднят и обсужден на моём форуме, посвящённом игре Wizard of Vegas .
Какова вероятность того, что шарик выпадет в точках 1, 2 и 3 за 4, 5, 6, 7, 8 или 9 вращений рулетки?
Общая формула такова:
Pr(Шар попадает в 1) + Pr(Шар попадает в 2) + Pr(Шар попадает в 3) - Pr(Шар попадает в 1 и 2) - Pr(Шар попадает в 1 и 3) - Pr(Шар попадает в 2 и 3) + Pr(Шар попадает в 1, 2 и 3).
В рулетке с двумя нулями при n количестве вращений это составляет 3*(1-(37/38)^n)-3*(1-(36/38)^n)+(1-(35/38)^n).
В следующей таблице показана вероятность выпадения всех трех чисел при различном количестве вращений от 3 до 100 для рулетки с одним и двумя нулями.
Вопрос по рулетке
| Вращения | Одинокий Ноль | Двойной Ноль |
|---|---|---|
| 3 | 0.000118 | 0.000109 |
| 4 | 0.000455 | 0.000420 |
| 5 | 0.001091 | 0.001009 |
| 6 | 0.002094 | 0.001939 |
| 7 | 0.003518 | 0.003261 |
| 8 | 0.005404 | 0.005016 |
| 9 | 0.007785 | 0.007234 |
| 10 | 0.010684 | 0.009937 |
| 15 | 0.033231 | 0.031066 |
| 20 | 0.068639 | 0.064476 |
| 25 | 0.114718 | 0.108254 |
| 30 | 0.168563 | 0.159750 |
| 35 | 0.227272 | 0.216265 |
| 40 | 0.288292 | 0.275379 |
| 45 | 0.349548 | 0.335089 |
| 50 | 0.409453 | 0.393835 |
| 55 | 0.466865 | 0.450467 |
| 60 | 0.521017 | 0.504191 |
| 65 | 0.571445 | 0.554501 |
| 70 | 0.617922 | 0.601122 |
| 75 | 0.660393 | 0.643951 |
| 80 | 0.698930 | 0.683016 |
| 85 | 0.733693 | 0.718435 |
| 90 | 0.764897 | 0.750386 |
| 95 | 0.792791 | 0.779086 |
| 100 | 0.817638 | 0.804773 |
В некоторых казино Мексики вместо колеса в рулетке используют игральные кости. Вот правила:
- В наборе четыре игральные кости — две зеленые, одна красная и одна синяя.
- Если оба зеленых кубика выпадут на единицу, то результат «вращения» будет равен нулю.
- Если на обоих зеленых кубиках выпадет шестерка, то результатом «вращения» будет двойной ноль.
- Если при броске зелёных кубиков произойдёт какой-либо другой исход, то 36 возможных исходов бросков красных и синих кубиков будут сопоставлены с числами 1 и 36, обозначающими «вращение».
Как это меняет шансы по сравнению с обычной рулеткой?
Вероятность выигрыша чисел 0 и 00 составит 1/36 для каждого. Если бы ставки на эти исходы приносили обычный выигрыш 35 к 1, то преимущество казино составило бы ровно 0%.
Вероятность выигрыша любого другого числа составит (34/36)*(1/36) = 2,62%. Сравните это с 1/38 = 2,63% в обычной рулетке с двумя нулями. Преимущество казино при любой ставке на числа от 1 до 36 составит 5,56%. Сравните это с 5,26% в обычной рулетке с двумя нулями. Мой совет в этой игре — ставить только на ноль и два нуля.
Если кто-либо может подтвердить или опровергнуть эти правила и оплатить их, пожалуйста, сообщите мне.
Я зафиксировал 7456 вращений рулетки. Результаты следующие. Я подозреваю, что колесо предвзято, но не уверен, достаточно ли убедительны эти данные, чтобы играть.
Данные рулетки
| Победа Число | События |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Общий | 7456 |
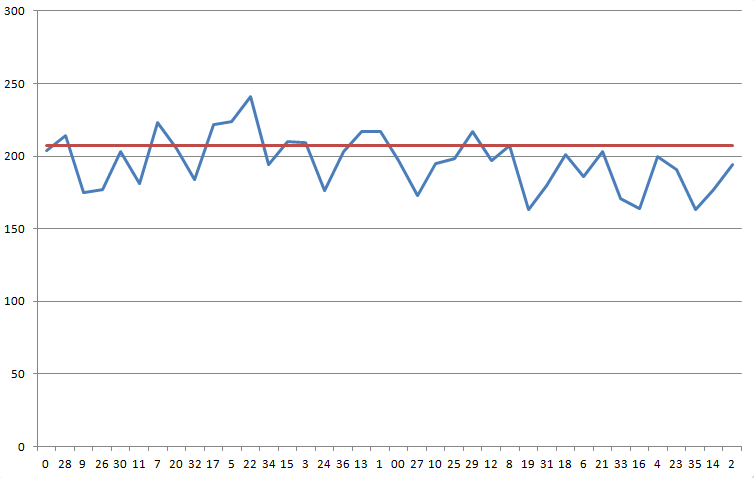
На следующем графике показаны ваши результаты в хронологическом порядке на колесе. Синяя линия показывает ваши результаты. Красная линия — это число, которое вам нужно, 207,11, чтобы преодолеть преимущество казино в 5,26%.
Критерий хи-квадрат для этого распределения дает статистику 68,1 при 37 степенях свободы. Вероятность того, что результат будет настолько или менее асимметричным, составляет 1 к 725.
Я не думаю, что критерий хи-квадрат идеально подходит для этой ситуации, потому что он не учитывает порядок результатов, но я не знаю лучшего критерия. Некоторые предлагали критерий Колмогорова-Смирнова , но я не думаю, что он подходит. Если есть какие-либо другие подходящие критерии, я с удовольствием их выслушаю.
Могу сказать, что если бы вы сделали ставку на дугу из 3 чисел вокруг числа 5, ваша прибыль составила бы 10,57% от зафиксированных вращений. Однако, если бы вы увеличили дугу до 7 чисел, преимущество снизилось бы до 2,84%.
Если бы меня попросили ответить простым и понятным языком, я бы сказал, что колесо демонстрирует признаки, но не неопровержимые доказательства, того, что оно предвзято. Однако этого предвзятости, вероятно, недостаточно, чтобы существенно и уверенно преодолеть преимущество казино. Предполагая, что казино не меняет колеса местами за столами, я бы сказал, что перед тем, как делать крупные ставки, следует собрать больше данных. Извините за такой уклончивый ответ.
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
В рулетке с одним нулем, каково среднее и медианное число вращений, необходимое для того, чтобы каждое число появилось хотя бы один раз?
Найти среднее арифметическое гораздо проще, поэтому начнём с этого. Давайте разберёмся шаг за шагом:
- Первый вращение, безусловно, принесет новый номер.
- Вероятность выпадения нового числа при втором вращении составляет 36/37. Если вероятность события равна p, то ожидаемое число испытаний, при которых оно произойдет, равно 1/p. В этом случае ожидаемое число испытаний для получения второго числа составляет 37/36 = 1,0278.
- После того, как были получены два числа, вероятность того, что следующий спин принесет новое число, составляет 35/37. Таким образом, ожидаемое количество вращений после второго числа, чтобы увидеть третье, составляет 37/35 = 1,0571.
- Следуя этой логике, среднее количество вращений для получения каждого числа составляет 1 + 37/36 + 37/35 + 37/34 + ... + 37/2 + 37/1 = 155,458690.
Медиана — гораздо более сложная задача. Чтобы найти точный ответ, в отличие от случайного моделирования, необходимо использовать множество матричных алгебраических вычислений. Я уже обсуждал, как решать подобные задачи в других вопросах рубрики «Спроси волшебника», поэтому не буду снова вдаваться в подробности. Один из примеров похожей задачи — это задача о получении пары 6-6 три раза подряд, как обсуждалось в вопросе «Спроси волшебника» № 311. Достаточно сказать, что вероятность увидеть каждое число за 145 вращений составляет 0,49161779, а за 146 вращений — 0,501522154. Таким образом, медиана равна 146.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Если в последних 20 вращениях рулетки шарик падал в красное поле, какова вероятность того, что в следующем вращении он упадет в черное поле?
То же самое, что и с красным, 47,37% на колесе с двумя нулями, 18 черных чисел, разделенных на 38 чисел в сумме.
Думаю, вы ошиблись с предыдущим вопросом. Вероятность выпадения 21 красного подряд составляет (18/38) 21 = 1 к 6 527 290. Вероятность должна быть подавляюще выше в пользу черного.
Это правда, но это не имеет значения. Вероятность выпадения 20 красных карточек за первой черной такая же. Дело в том, что прошлое не имеет значения в играх, основанных на независимых испытаниях, таких как рулетка.
Я придумал способ обыграть казино в рулетку! Начните с небольшой ставки на любую ставку с равными шансами, например, на красное или чёрное. Если проиграет, удвойте ставку на то же самое. Затем продолжайте удваивать ставку, пока не выиграет. Выигрышный исход должен когда-нибудь произойти, и когда это случится, я получу прибыль от своей первоначальной ставки. Затем повторите. Каково ваше мнение? И пожалуйста, никому не рассказывайте.
Вероятно, это самая популярная из всех систем ставок, известная как система Мартингейла. Игроки придумали и использовали её с незапамятных времён. Как и все системы ставок, она не только не превосходит преимущество казино, но и даже не уменьшает его. Причина в том, что у игрока рано или поздно начнётся полоса неудач, когда его банкролла не хватит, чтобы удвоить ставку.
В своем предыдущем ответе вы объяснили, почему стратегия Мартингейла не работает. Тогда как насчет обратного варианта: удваивать ставку после каждого выигрыша, пока не будет достигнута желаемая цель?
Это называется анти-Мартингейлом и тоже совершенно бесполезно. Время, когда ваш банкролл истощается до нуля, перевесит выигрыш, когда вы достигнете своей цели. Независимо от того, какую систему ставок вы используете или не используете вообще, чем больше вы играете, тем ближе соотношение проигранных денег к поставленным будет к 5,26% в рулетке с двойным зеро.
Каково ожидаемое количество вращений рулетки, при которых подряд выпадут пять красных или пять черных чисел?
[спойлер] Ответ: 3872789/118098 ≈ 32,79301089 вращений. [/spoiler]
Вот моё решение (PDF).
Что такое «закон третей» в рулетке?
«Закон третей» гласит, что если вы вращаете рулетку один раз для каждого выпавшего числа, то примерно 1/3 чисел никогда не выпадут.
1/3 — это довольно неточная оценка. Гораздо лучше было бы 1/e ≈ 36,79%. Истинный процент в рулетке с двумя нулями составляет 36,30%.
В следующей таблице показана вероятность выпадения от 1 до 38 различных чисел за 38 вращений рулетки с двумя нулями.
Закон третей — Рулетка с двумя нулями
| Отчетливый Числа | Вероятность |
|---|---|
| 1 | 0.000000000 |
| 2 | 0.000000000 |
| 3 | 0.000000000 |
| 4 | 0.000000000 |
| 5 | 0.000000000 |
| 6 | 0.000000000 |
| 7 | 0.000000000 |
| 8 | 0.000000000 |
| 9 | 0.000000000 |
| 10 | 0.000000000 |
| 11 | 0.000000000 |
| 12 | 0.000000000 |
| 13 | 0.000000005 |
| 14 | 0.000000124 |
| 15 | 0.000001991 |
| 16 | 0.000022848 |
| 17 | 0.000191281 |
| 18 | 0.001186530 |
| 19 | 0.005519547 |
| 20 | 0.019434593 |
| 21 | 0.052152293 |
| 22 | 0.107159339 |
| 23 | 0.169042497 |
| 24 | 0.204864337 |
| 25 | 0.190490321 |
| 26 | 0.135436876 |
| 27 | 0.073211471 |
| 28 | 0.029838199 |
| 29 | 0.009063960 |
| 30 | 0.002020713 |
| 31 | 0.000323888 |
| 32 | 0.000036309 |
| 33 | 0.000002742 |
| 34 | 0.000000132 |
| 35 | 0.000000004 |
| 36 | 0.000000000 |
| 37 | 0.000000000 |
| 38 | 0.000000000 |
| Общий | 1.000000000 |
В таблице показано, что наиболее вероятный исход — 24 различных числа, что составляет 20,49%. Среднее значение равно 24,20656478.
Некоторые шарлатаны утверждают, что игрок должен наблюдать за первыми девятью различными исходами, а затем делать на них ставки, ошибочно полагая, что они более вероятны, чем другие числа. Это совершенно неверно! Колесо и шарик не обладают памятью. На честном колесе каждое число имеет одинаковую вероятность, и прошлое не имеет значения.