Спросите Волшебника #259
В некоторых казино Голландии разрешено тройное заключение в рулетке. Каково преимущество казино при ставках с равными шансами по этому правилу? Меня больше интересует решение, чем ответ.
Для справки, во многих европейских казино, если вы делаете ставку с равными шансами в рулетке, и шарик останавливается на нулевой отметке, то ставка блокируется. Если следующий бросок принесет выигрыш, то ставка возвращается без выигрыша. Если шарик останавливается в противоположную сторону, то ставка проигрывает.
Что происходит с одиночными ставками, если шарик попадает в ноль? Если казино разрешает только одиночные ставки, то они проиграют. Однако некоторые казино разрешают двойные ставки, что и происходит. Если ставка с двойными ставками выигрывает, то она возвращается к одиночной. Если казино разрешает только до двойных ставок, то ставка с двойными ставками проиграет при попадании в другой ноль. По той же логике, если казино разрешает тройные ставки, то ставка с двойными ставками станет тройной ставкой при попадании в другой ноль.
Преимущество казино при тройном заключении составляет 1,370120%. Прежде чем объяснить, как я к этому пришел, давайте сначала рассмотрим одинарное и двойное заключение. Предположим, первая ставка сделана на красное.
Пусть Z = вероятность выпадения нуля = 1/37.
Пусть R = вероятность выпадения красного числа = 18/37.
Одиночное заключение
pr(push) = ZR = 0.0131482834.
pr(win) = R = 0.4864864865.
пр(проигрыш) = 1-пр(толчок)-пр(выигрыш) = 0,5003652301.
Ожидаемое значение = pr(выигрыш) - pr(проигрыш) = -0,0138787436.
Двойное заключение
Игрок сделает «нулевой» ход, если первый спин принесет ноль, затем игрок может повторять ZR от 0 до бесконечного числа раз, а затем получить красный цвет. Другими словами, способы сделать «нулевой» ход следующие:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
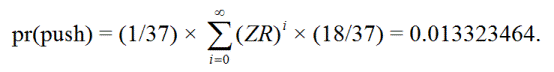
pr(push) = 0.013323464
pr(win) = 18/37 = 0,4864864865.
пр(проигрыш) = 1-пр(толчок)-пр(выигрыш) = 0,5001900494.
Ожидаемое значение = pr(выигрыш) - pr(проигрыш) = -0,0137035629.
Тройное заключение
Сначала найдем вероятность p1 того, что одиночная ставка, находящаяся в состоянии "заключения", превратится в тройную ставку с двумя дополнительными нулями, а затем в конечном итоге снова вернется в состояние "заключения одной". Это может произойти следующим образом:
ЗЗРР, ЗЗ(РЗ)РР, ЗЗ(РЗ)(РЗ)РР, ЗЗ(РЗ)(РЗ)(РЗ)РР, ...
Иными словами, ставка может меняться от тройного до двойного тюремного заключения бесконечное количество раз.
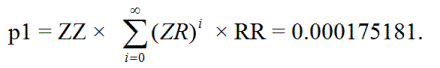
Во-вторых, пусть p 2 = вероятность того, что одиночная заключенная по пари достигнет первого или второго уровня тюремного заключения, а затем вернется к одиночному заключению.
Пусть p 2 = ZR + p 1 = 0,013323464.
Игрок может бесконечное количество раз возвращаться на первый уровень с нуля. Таким образом, вероятность толчка составляет:
ZR + Z p 2 R + Z p 2 p 2 R + Z p 2 p 2 p 2 R + ... =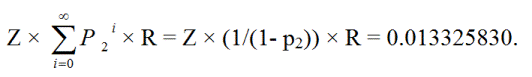
Z × (1/(1- p 2 )) × R = 0.013325830.
pr(push) = 0.013325830.
pr(win) = 18/37 = 0,4864864865.
пр(проигрыш) = 1-пр(толчок)-пр(выигрыш) = 0,5001876839.
Ожидаемое значение = pr(выигрыш) - pr(проигрыш) = -0,0137011974.
Бесконечное заключение
Не то чтобы ты спрашивал, Мафф, но я слышал, что в Испании разрешают бесконечное тюремное заключение. Пусть p = вероятность толчка. Это также вероятность начать с уровня заключения x, спускаться по уровням ниже, но в конечном итоге снова подняться до x.
р = ЗР + ЗпР + ЗппР + ЗпппР + ...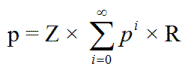
p 2 - p + ZR = 0
По квадратичной формуле p = (1-(1-4*RZ) 1/2 )/2 = 0,0133258620.
pr(push) = 0.0133258620.
pr(win) = 18/37 = 0,4864864865.
пр(проигрыш) = 1-пр(толчок)-пр(выигрыш) = 0,5001876515.
Ожидаемое значение = pr(выигрыш) - pr(проигрыш) = -0,0137011650.
Нули игнорировали тюремное заключение
Наконец, в некоторых казино нули просто игнорируются после первого нуля, что блокирует ставку. Там вероятность ничьей составляет всего (1/37)×(1/2) = 0,0135135135.
В следующей таблице приведено краткое описание всех четырех типов правил.
Вероятность тюремного заключения
| Тюремное заключение | Победить | Толкать | Потеря | Ожидал Ценить |
| Одинокий | 0.48648649 | 0.01314828 | 0.50036523 | -0.01387874 |
| Двойной | 0.48648649 | 0.01332346 | 0.50019005 | -0.01370356 |
| Тройной | 0.48648649 | 0.01332583 | 0.50018768 | -0.01370120 |
| Бесконечность | 0.48648649 | 0.01332586 | 0.50018765 | -0.01370117 |
| Нули игнорируются | 0.48648649 | 0.01351351 | 0.50000000 | -0.01351351 |
Я хотел бы поблагодарить ChesterDog и weaselman за их математическую помощь. Также я хотел бы выразить благодарность и упомянуть профессора Г. Артико и polarprof.it за HTML-версию формулы суммирования, приведенной выше.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Пожалуйста, примите во внимание, что следующее утверждение справедливо для одного видеопокерного автомата.
- 6-5 Бонусный покер с прогрессивным джекпотом.
- Повышение цены на роял-флеш на 2%.
- Игра с 5 монетами.
Теперь предположим следующее обо мне.
- Минимальный возврат инвестиций составляет 100,5%.
- Я способен играть на прогрессивной пружине, пока не добьюсь успеха.
- Я знаю идеальную стратегию игры в покер 6-5 Bonus для роял-сбора в 4000 монет.
Каков минимальный размер джекпота, чтобы я мог играть?
7 281,8 монет. Интересно отметить, что если бы вы сыграли всего один раз ровно на этом уровне, то выигрыш составил бы всего 98,5%. Причина, по которой стоит играть на этом уровне, заключается в предположении, что вы способны играть до тех пор, пока не сорвете джекпот. Это как иметь клуб игровых автоматов с 2% кэшбэком. 98,5% + 2% = 100,5%.
Добавлю, что если начать играть по стратегии с джекпотом в 4000 монет, имея ровно 7281,8 монет, то можно ожидать прибыли в 201,18 монет. Однако, если бы вы потратили время на изучение изменений стратегии для джекпота в 7281,8 монет, то ваша ожидаемая прибыль составила бы 234,31 монет.
Кстати, я только что закончил читать книгу Фрэнка Ниленда «Тайный мир прогрессивного видеопокера» . В этой книге много формул для гораздо более сложных ситуаций с прогрессивными джекпотами, а также практические советы и истории, основанные на его многолетнем опыте руководства командой охотников за прогрессивными джекпотами. Я рекомендую её игрокам в видеопокер с преимуществом.
В казино в Оклахоме в шестиколодную колоду блэкджека помещают три джокера. Как это повлияет на шансы?
В своей книге «Базовый блэкджек» Стэнфорд Вонг рассматривает джокеров в блэкджеке. Там он утверждает, что каждый джокер в колоде приносит игроку 4,2% от его стоимости. Таким образом, половина джокера в колоде будет стоить 2,1%. В его книге содержится стратегия определения того, какую карту объявить джокером, в зависимости от других карт игрока и открытой карты дилера.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Существуют ли какие-либо опросы или данные, которые бы подробно описывали, какой процент игр в блэкджек в Лас-Вегасе приходится на ставки 6-5 или любые другие «карнавальные» вариации?
Согласно информационному бюллетеню Current Blackjack Newsletter за сентябрь 2010 года, в Лас-Вегасе насчитывалось 2099 столов для игры в блэкджек. В следующей таблице показано, сколько из них представляли собой четыре наиболее популярные разновидности блэкджека.
Варианты блэкджека в Лас-Вегасе
| Игра | Таблицы | Процент |
| 6 до 5 | 467 | 22,2% |
| Смена блэкджека | 42 | 2,0% |
| Супер Веселье 21 | 41 | 2,0% |
| Испанский 21 | 6 | 0,3% |
| Общий | 556 | 26,5% |
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .


