Спросите Волшебника #261
Какие факторы влияют на ставки на тотал в футболе по мере развития сезона, ухудшения погоды и появления большего количества информации о последних результатах команд? Насколько легко (или сложно) обнаружить ошибки в коэффициентах?
Чтобы помочь ответить на этот вопрос, я построил график среднего количества очков, набранных в зависимости от номера недели в НФЛ, на основе данных за каждый сезон с 1983 по 2009 год. На следующем графике представлены результаты.
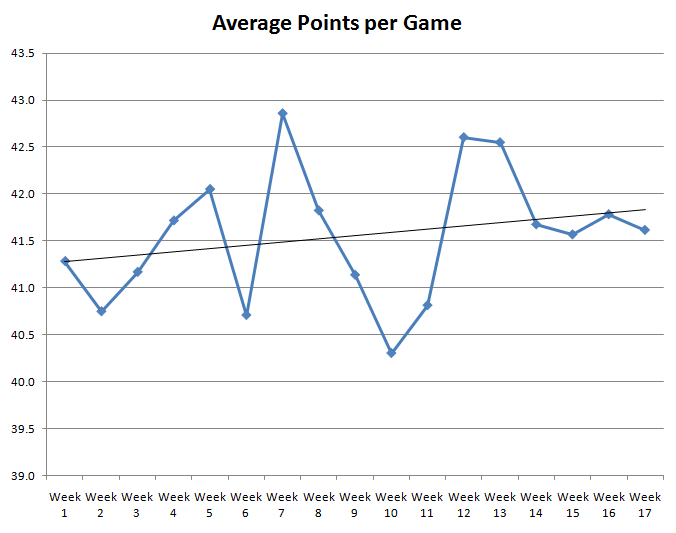
Как видите, линия сильно колеблется вверх и вниз. Тонкая черная линия — это линия наилучшего соответствия методом наименьших квадратов, которая показывает общую тенденцию к росту. Таким образом, по мере смены сезонов и понижения температуры среднее количество набранных очков немного увеличивается, но это вполне может быть случайным колебанием.
На этом я, пожалуй, и закончу. Чтобы получить общее представление о том, как погода влияет на спортивные ставки в целом, я обратился к своему другу Джейсону Бину, который является экспертом в этой области. Вот что он сказал:
В большинстве случаев ветер является основным погодным фактором, наиболее сильно влияющим на игру; но это не единственный фактор. В бейсболе и других видах спорта на открытом воздухе тени могут оказывать не меньшее влияние, особенно во время дневных бейсбольных матчей в начале и конце сезона. Дождь или снег не являются таким уж большим фактором в американском футболе, как многие думают, поскольку они, как правило, одинаково влияют как на нападение, так и на защиту. Например, защитник против принимающего. Дождь и снег одинаково замедлят их, не давая ни одной из сторон преимущества. Ветер может просто сорвать игру в пас в американском футболе, как и удары ногой. Я видел игры, где команда, играющая в пас, была вынуждена почти в каждом розыгрыше бежать с мячом из-за сильного бокового ветра. Это случается нечасто, но иногда ветер становится решающим фактором в игре.Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
Что обычно происходит в крэпсе, если игрок делает слишком большую ставку, чем положено, и дилеры не замечают этого до тех пор, пока ставка не выиграет или не проиграет?
Я спросил об этом бывшего менеджера игровых столов в Вегасе. Он сказал, что часть ставки на коэффициенты, превышающая допустимый множитель ставки на линию, будет выплачиваться по коэффициентам ставок на места. Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В НФЛ, в среднем, какова вероятность того, что после забитого мяча следом забьет другая команда?
Исходя из данных по сезонам НФЛ 2000-2009 годов, ответ — 57%.
Рассмотрим дуэль (тройную дуэль) с участием А, В и С. Они сражаются насмерть за женщину. Все они — джентльмены, и все они согласны со следующими правилами.
- Три участника образуют треугольник.
- В каждом только один патрон.
- Сначала идет А, затем В и В.
- Вероятность попадания снаряда А в намеченную цель составляет 10%.
- Вероятность попадания точки B в намеченную цель составляет 60%.
- Вероятность попадания цели у цели C составляет 90%.
- Случайных выстрелов не было.
- Стрельба в воздух (намеренный промах) и стрельба в себя разрешены и всегда успешны.
- Если после любого раунда остаются два или три выживших, каждому выдается новый патрон. Затем они по очереди стреляют в том же порядке, пропуская тех, кто уже погиб.
- Все три участника — превосходные логики.
На кого должен нацелиться А в первую очередь? Какова вероятность его выживания в отношении каждой из первоначальных целей?
Эта головоломка обсуждается в программе BBC «Quite Interesting» . Прокрутите страницу вниз на 100 строк, чтобы увидеть ответ и решение.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Вот мои вероятности победы А в зависимости от каждой начальной цели. Как видите, вероятность победы А максимальна при преднамеренном выстреле в воздух.
Коэффициенты Труэла
| Стратегия | Вероятная победа |
| Воздух | 13,887% |
| А | 0,000% |
| Б | 12,560% |
| С | 13,094% |
Для решения задачи будем использовать обозначение Pr(X) для вероятности того, что после раунда останется только группа X. Обозначим вероятность того, что группа X в итоге выиграет раунд, повторяя ходы до тех пор, пока состояние игры не изменится из-за попадания в кого-либо из игроков. Пусть Pr(X**) — вероятность того, что игрок X — единственный выживший. Чтобы найти окончательные вероятности, рассмотрим сначала состояния двух игроков. Очевидно, что каждый будет стрелять в другого.
А против В
- Pr(A) = 0,1
- Pr(B) = 0,9 × 0,6 = 0,54
- Pr(AB) = 0,9 × 0,4 = 0,36
Если выживут оба, то процесс будет повторяться до тех пор, пока не останется только один выживший. Таким образом, вероятности того, что вы станете последним выжившим, таковы:
- Пр(А*) = Пр(А)/(1-Пр(АВ)) = 0,1/0,64 = 0,15625
- Пр(В*) = Пр(В)/(1-Пр(АВ)) = 0,54/0,64 = 0,84375
А против С
- Pr(A) = 0,1
- Pr(C) = 0,9 × 0,9 = 0,81
- Pr(AC) = 0,9 × 0,1 = 0,09
Если выживут оба, то процесс будет повторяться до тех пор, пока не останется только один выживший. Таким образом, вероятности того, что вы станете последним выжившим, таковы:
- Пр(А*) = Пр(А)/(1-Пр(АС)) = 0,1/0,91 = 0,10989011
- Пр(С*) = Пр(Б)/(1-Пр(АС)) = 0,81/0,91= 0,89010989
B против C
- Pr(B) = 0,6
- Pr(C) = 0,4 × 0,9 = 0,36
- Pr(BC) = 0.$×0.1 = 0.04
Если выживут оба, то процесс будет повторяться до тех пор, пока не останется только один выживший. Таким образом, вероятности того, что вы станете последним выжившим, таковы:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0,6/0,96 = 0,625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0,36/0,96= 0,375
Теперь мы готовы проанализировать случай с тремя игроками. Рассмотрим ситуацию, когда А целится в В.
Три игрока — А целится в Б
Если А попадёт в В, то С точно выживет, а может и не выживет. Таким образом, два возможных исхода попадания в В — это AC и C. Если А промахнётся мимо В, то В будет целиться в более опасную цель — С. Если В попадёт в С, то А и В выживут. Если В промахнётся мимо С, то С будет целиться в более опасную цель — В. Если С промахнётся мимо В, то выживут все трое. Если С попадёт в В, то А и С выживут. Таким образом, возможные исходы — это C, AB, AC и ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0,1 × 0,9 = 0,09. Это достигается ударом A по B, а затем ударом C по A.
- Pr(AB) = 0,9 × 0,6 = 0,54. Это достигается, когда A промахивается мимо B, а затем B попадает в C.
- Pr(AC) = 0,1 × 0,1 + 0,9 × 0,4 × 0,9 = 0,334. Этого можно достичь двумя способами. Первый — удар А по В, а затем удар С мимо А. Второй — удар А мимо В, удар В мимо С, а затем удар С по В.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Это достигается при отсутствии всех трех элементов.
По той же логике, что и в случаях с двумя игроками, мы можем разделить каждый исход на (1-Pr(ABC))=0,964, чтобы найти вероятности каждого состояния, предполагая, что состояние игры изменилось после раунда.
- Пр(С*) = 0,09/0,964 = 0,093361.
- Пр(АВ*) = 0,54/0,964 = 0,560166.
- Пр(АС*) = 0,334/0,964 = 0,346473.
Из случаев с двумя игроками мы знаем, что если в итоге выберут A и B, то A победит с вероятностью 0,15625, а B — с вероятностью 0,84375. Если в итоге выберут A и C, то A победит с вероятностью 0,109890, а C — с вероятностью 0,890110.
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. A может стать победителем двумя способами: (1) достигнув состояния AB и затем выиграв, или (2) достигнув состояния AC и затем выиграв.
- Pr(B**) = 0,560166 × 0,84375 = 0,472640. B станет победителем, если достигнет состояния AB, и тогда B победит.
- Pr(C**) = 0,093361 + (0,346473 × 0,890110) = 0,401760. C может победить, если A убьет B, а затем C убьет A в первом раунде, или если C достигнет состояния AC, а затем C победит.
Таким образом, если стратегия А состоит в том, чтобы сначала нацелиться на В, то вероятность того, что он окажется единственным выжившим, составляет 12,56%.
Три игрока — А целится в С
Если А попадёт в С, то В точно выживет, а может и не выживет. Таким образом, два возможных исхода попадания в С — это AB и B. Если А промахнётся мимо С, то В будет целиться в более опасную цель — С. Если В попадёт в С, то А и В выживут. Если В промахнётся мимо С, то С будет целиться в более опасную цель — В. Если С промахнётся мимо В, то выживут все трое. Если С попадёт в В, то А и С выживут. Таким образом, возможные исходы — это B, AB, AC и ABC.
- Pr(A) = 0.
- Pr(B) = 0,1 × 0,6 = 0,06.
- Pr(C) = 0.
- Pr(AB) = (0,1 × 0,4) + (0,9 × 0,6) = 0,04 + 0,54 = 0,58. Этого можно достичь двумя способами.Первый случай: А попадает в С, а затем В промахивается мимо А. Второй случай: А промахивается мимо В, а затем В попадает в С.
- Pr(AC) = 0,9 × 0,4 × 0,9 = 0,324. Это достигается за счет того, что A не попадает в C, B не попадает в C, и C попадает в B.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Это достигается при отсутствии всех трех элементов.
По той же логике, что и в случаях с двумя игроками, мы можем разделить каждый исход на (1-Pr(ABC))=0,964, чтобы найти вероятности каждого состояния, предполагая, что состояние игры изменилось после раунда.
- Пр(В*) = 0,06/0,964 = 0,062241.
- Пр(АВ*) = 0,58/0,964 = 0,601660.
- Пр(АС*) = 0,324/0,964 = 0,336100.
По той же логике, что и решение для случая, когда цель А — цель Б:
- Пр(А**) = (0,601660 × 0,15625) + (0,336100 × 0,10989011) = 0,130943.
- Pr(B**) = 0,062241 + 0,601660 × 0,84375 = 0,569891.
- Пр(С**) = 0,336100 × 0,890110 = 0,299166.
Таким образом, если стратегия А состоит в том, чтобы сначала нацелиться на С, то вероятность того, что он окажется единственным выжившим, составляет 13,09%.
Три игрока — промахнулись намеренно.
После того, как А намеренно промахнется, В будет целиться в более опасную цель С. Если В попадет в С, то А и В выживут. Если В промахнется в С, то С будет целиться в более опасную цель В. Если С промахнется в В, то выживут все трое. Если С попадет в В, то А и С выживут. Таким образом, возможные исходы — AB, AC и ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0,6. Это достигается ударом B по C.
- Pr(AC) = 0,4 × 0,9 = 0,36. Это достигается, когда B промахивается мимо C, а затем C попадает в B.
- Pr(BC) = 0.
- Pr(ABC) = 0,4 × 0,1 = 0,04. Это достигается при отсутствии всех трех элементов.
По той же логике, что и в случаях с двумя игроками, мы можем разделить каждый исход на (1-Pr(ABC))=0,96, чтобы найти вероятности каждого состояния, предполагая, что состояние игры изменилось после раунда.
- Pr(AB*) = 0,6/0,96 = 0,625.
- Pr(AC*) = 0,36/0,96 = 0,375.
По той же логике, что и решение для случая, когда цель А — цель Б:
- Пр(А**) = (0,625 × 0,15625) + (0,375 × 0,109890) = 0,138865.
- Пр(Б**) = 0,625 × 0,84375 = 0,527344.
- Пр(С**) = 0,375 × 0,890110 = 0,333791.
Таким образом, если стратегия А состоит в том, чтобы сначала нацелиться на С, то вероятность того, что он окажется единственным выжившим, составляет 13,89%.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .


