Спросите Волшебника #265

Вы путаете среднее арифметическое и медиану. Давайте рассмотрим мою ситуацию в качестве примера. Мне 45 лет, я мужчина. Моя ожидаемая продолжительность жизни составляет 78,11 лет, но при этом у меня всего 50,04% шансов дожить до 80 лет.

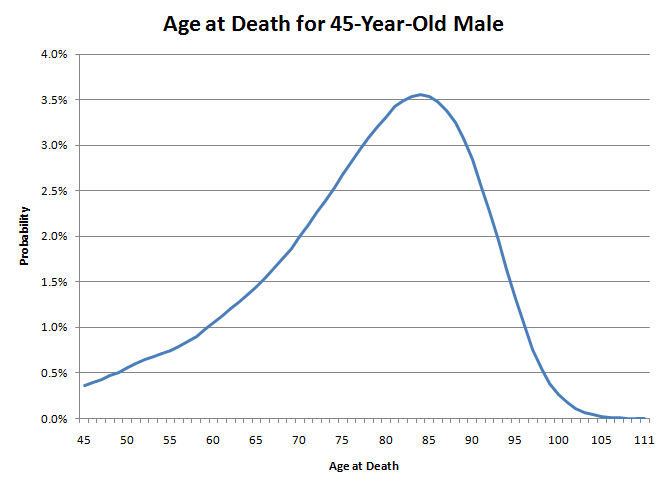
Мой возраст смерти будет подобен броску дротика в этот график. Обратите внимание, что левый хвост намного толще правого. Это означает, что вероятность моей смерти сейчас довольно низка. Однако с возрастом вероятность смерти в следующем году будет только расти. Например, для 45-летнего мужчины вероятность дожить до 46 лет довольно высока и составляет 99,64%. Однако в 85 лет вероятность дожить до 86 составляет всего 89,21%. Это как природа, медленно втыкающая вам нож в спину. Сначала это, вероятно, вас не убьет, но с каждым годом вероятность постепенно увеличивается. Однако, как только вы достигнете возраста около семидесяти лет, природа скажет: «Хватит игр», и начнет действительно втыкать нож.

Таким образом, если множество 45-летних мужчин бросить дротики в этот график, 49,96% попадут в диапазон от 45 до 79 лет, а 50,04% — от 80 до 111 лет. Однако счастливая половина, попавшая в правую часть графика, вероятно, не доживет намного до 80 лет. После 80 лет мужчина может рассчитывать прожить всего 7,78 лет. Между тем, многие из несчастной половины, не дожившие до 80 лет, умрут гораздо раньше. Таким образом, именно многочисленные смерти в молодом возрасте снижают среднюю продолжительность жизни.

В аналогичной ситуации рассмотрим игральную кость с номерами 10, 20, 30, 31, 32, 33. Среднее значение равно 26, однако вероятность выпадения большего числа составляет 2/3.

В качестве примера различия между средним значением и медианой, предположим, что мы добавим в выборку еще две смерти. Одна в возрасте 46 лет, другая в 81 год. Вероятность дожить до 80 лет не изменится, но средняя ожидаемая продолжительность жизни в возрасте 45 лет снизится.

Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .

Хороший вопрос. В правилах казино говорится о разделении пяти тузов, при этом в младшей руке разыгрываются два туза. Исключение составляет сохранение пяти одинаковых карт в старшей руке, если в младшей руке можно разыграть двух королей. На моей странице, посвященной пай-гоу-покеру, указаны семь правил казино из Лас-Вегаса и Атлантик-Сити, и все они включают это исключение. Три правила из-за пределов этих двух городов его не включают.

Вероятность получить четыре туза, джокера и двух королей составляет 1 к 25 690 513. Если предположить, что дилер является банком, то это исключение пригодится только в том случае, если у игрока в старшей руке четыре одинаковые карты или лучше. Вероятность этого составляет примерно 1 к 300. Вероятность того, что произойдет и то, и другое, составляет примерно 1 к 7,6 миллиардам.

Согласно данным Комиссии по контролю за азартными играми штата Невада, в 2009 году в Неваде насчитывалось 306 столов для игры в пай-гоу-покер. Если предположить, что раздача происходит 60 раздач в час, за каждым столом играют два игрока, и все столы открыты круглосуточно, то для того, чтобы это исключение произошло и повлияло на результат, потребуется 23,7 года.

Таким образом, казино требуют от каждого дилера пай гоу покера запомнить это исключение, хотя, возможно, оно никогда не влияло на исход игры за всю её историю. Я предполагаю, что тот же человек, который придумал добавить это правило, решил, что стрит A2345, известный как «колесо», является вторым по старшинству стритом.

Это классическая задача в истории теории вероятностей. Многие ошибочно считают, что ответ — 18, потому что вероятность выпадения 12 составляет 1 к 36, а 18 × (1/36) = 50%. Однако, по этой логике, вероятность выпадения 12 из 36 бросков должна составлять 100%, что явно не так. Вот правильное решение. Пусть r — количество бросков. Вероятность того, что выпадет не 12, равна 35/36. Вероятность того, что из r бросков выпадет 0 12, равна (35/36) ^r . Таким образом, нам нужно найти r в следующем уравнении:

(35/36) ^r = 0,5
log(35/36) ^r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24,6051

Таким образом, округленного ответа нет. Вероятность выпадения 12 при 24 бросках составляет 1-(35/36) ²⁴ = 49,14%. Вероятность выпадения 12 при 25 бросках составляет 1-(35/36) ²⁵ = 50,55%.

Если вы хотите сделать ставку, допустим, вы сможете выбросить 12 за 25 бросков, или кто-то другой не сможет за 24 броска. В любом случае, у вас будет преимущество при равных шансах.

Я бы поставил 10 к 1 на то, что вам выплатят, хотя они, возможно, сначала немного с вами поговорят. Причина моих сомнений в том, что букмекерская контора может отменить ставку, которая явно была сделана по ошибке, с разрешения Комиссии по контролю за азартными играми.

«Библиотека не может в одностороннем порядке аннулировать ставку без предварительного письменного согласия председателя». — Постановление штата Невада 22.115

Хотя это право существует, судя по имеющимся данным, им пользуются крайне редко. Сообщите мне, что произойдет.

P.S. Позже задавший вопрос сообщил мне, что ему заплатили без особых проблем.

Да, это произойдёт через e ^{100 000} -1 секунд. См. мой сайт mathproblems.info , задача 206, там два решения.

Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .