Спросите Волшебника #307
Я участвую в «пуле прогнозов на 2018 год». Вот правила:
- Каждый участник должен предоставить список из десяти ныне живущих знаменитостей в возрасте до 100 лет.
- Если в 2018 году умрет какая-либо знаменитость, как это подтверждает Associated Press, то любой, чье имя есть в списке, получит 100-x баллов, где x — возраст на момент смерти.
- Побеждает игрок, набравший наибольшее количество очков по состоянию на 1 января 2019 года.
Исходя из средних значений, какая стратегия является оптимальной для этой игры?
Как бывший актуарий, вы обратились к нужному человеку. Надеюсь, Общество актуариев не сочтет мой ответ злоупотреблением профессией. Тем не менее, чтобы ответить на ваш вопрос, я обратился к таблице продолжительности жизни за 2014 год из моего бывшего места работы, Управления главного актуария Управления социального обеспечения.
Таблица продолжительности жизни показывает, помимо прочего, вероятность смерти для человека любого возраста и пола в 2014 году. Используя эту информацию, я создал следующую таблицу, которая показывает как вероятность смерти, так и ожидаемые значения для всех возрастов от 0 до 100 лет и обоих полов.
Таблица продолжительности жизни за 2014 год. Фонд страхования от смерти.
| Возраст | Вероятность Смерть — Мужская | Вероятность Смерть — Женщина | Ожидал Баллы — Мужской | Ожидал Баллы — Женщина |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0,001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
В таблице показано, что максимальное ожидаемое количество баллов для 90-летнего мужчины составляет 1,645220.
Этот вопрос поднимается и обсуждается на моем форуме, не посвященном азартным играм, Diversity Tomorrow .
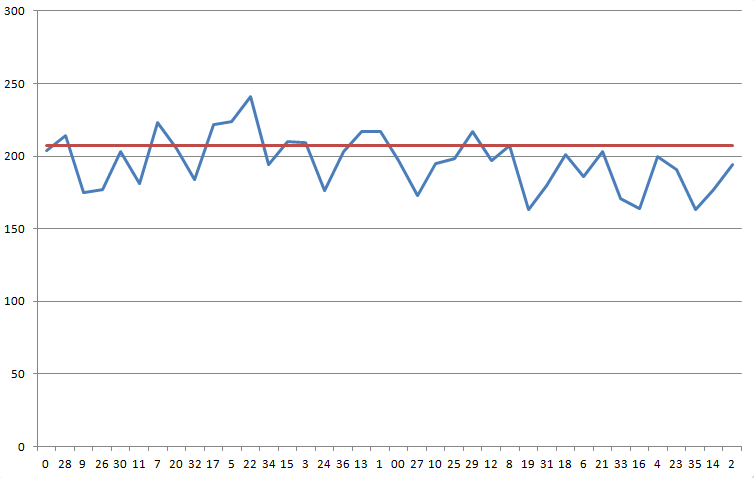
Я зафиксировал 7456 вращений рулетки. Результаты следующие. Я подозреваю, что колесо предвзято, но не уверен, достаточно ли убедительны эти данные, чтобы играть.
Данные рулетки
| Победа Число | События |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Общий | 7456 |
На следующем графике показаны ваши результаты в хронологическом порядке на колесе. Синяя линия показывает ваши результаты. Красная линия — это число, которое вам нужно, 207,11, чтобы преодолеть преимущество казино в 5,26%.
Критерий хи-квадрат для этого распределения дает статистику 68,1 при 37 степенях свободы. Вероятность того, что результат будет настолько или менее асимметричным, составляет 1 к 725.
Я не думаю, что критерий хи-квадрат идеально подходит для этой ситуации, потому что он не учитывает порядок результатов, но я не знаю лучшего критерия. Некоторые предлагали критерий Колмогорова-Смирнова , но я не думаю, что он подходит. Если есть какие-либо другие подходящие критерии, я с удовольствием их выслушаю.
Могу сказать, что если бы вы сделали ставку на дугу из 3 чисел вокруг числа 5, ваша прибыль составила бы 10,57% от зафиксированных вращений. Однако, если бы вы увеличили дугу до 7 чисел, преимущество снизилось бы до 2,84%.
Если бы меня попросили ответить простым и понятным языком, я бы сказал, что колесо демонстрирует признаки, но не неопровержимые доказательства, того, что оно предвзято. Однако этого предвзятости, вероятно, недостаточно, чтобы существенно и уверенно преодолеть преимущество казино. Предполагая, что казино не меняет колеса местами за столами, я бы сказал, что перед тем, как делать крупные ставки, следует собрать больше данных. Извините за такой уклончивый ответ.
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
У двух игроков, Сэма и Дэна, по пять монет. Каждый должен выбрать, какую из них положить в руку — от одной до пяти монет. При этом каждый должен показать количество сыгранных монет. Если оба выберут одинаковое количество монет, то Сэм выиграет и заберет все сыгранные монеты. Если оба выберут разное количество монет, то Дэн заберет все сыгранные монеты. Предполагая, что оба игрока — совершенные логики, какова оптимальная стратегия для Дэна?
Дэну следует рандомизировать свою стратегию следующим образом:
- Вероятность выпадения одной монеты = 77/548.
- Вероятность выпадения одной монеты = 107/548.
- Вероятность выпадения одной монеты = 117/548.
- Вероятность выпадения одной монеты = 122/548.
- Вероятность выпадения одной монеты = 125/548.
Применяя эту стратегию, Дэн может рассчитывать на выигрыш в 3,640510949 монет каждый ход, независимо от того, сколько монет выберет Сэм.
Решение можно найти на моем сайте с математическими задачами , задача 230.
Аналогичный вопрос, который привёл к этому, можно найти на моём форуме Wizard of Vegas .
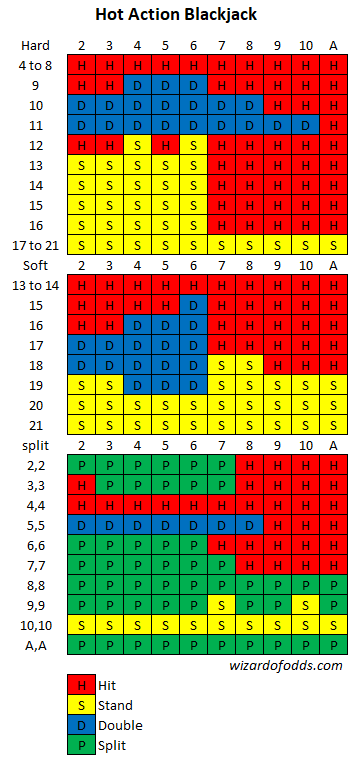
В казино California Grand в Сан-Франциско проходит игра в блэкджек под названием Hot Action Blackjack. Правила игры следующие:
- Шесть колод в непрерывном перемешивании с дополнительными 18 джокерами номиналом 2.
- Дилер набрал 17 очков, что является слабым результатом.
- Удваивайте ставку на любые первые 2 карты.
- Можно разделить до четырех рук.
- Перераспределение тузов или их повторное разделение не допускается.
- Сдаваться нельзя.
- Выплаты в блэкджеке составляют 6 к 5.
- Если первые две карты игрока — джокеры, то он получает бонус 4 к 1.
- Если первые две карты игрока — одномастные тузы, то он получает бонус 5 к 1.
- Для участия в игре игрок должен заплатить комиссию в размере 5%.
В чём заключается основная стратегия и каково преимущество казино?
Во-первых, вот моя основная стратегия, основанная на этих правилах:
Учитывая все обстоятельства, я показываю преимущество казино в 6,01% (ой!) исходя из первоначальной ставки. Другими словами, если игрок поставит 100 долларов, не считая комиссии в 5 долларов, то он может проиграть 6,01 доллара. Это показывает, почему я бы избегал игр с участием игроков за счет дилера в Калифорнии, если только вы сами не являетесь дилером.
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .