Спросите Волшебника #313
Какова дисперсия в игре «Келопатра Кено» ?
Напоминаем нашим читателям, что игра в Клеопатру Кено похожа на обычное кено, за исключением того, что если последний вытянутый шар совпадает с одним из выбранных игроком шаров И приводит к выигрышу, то игрок также получает 12 бесплатных игр с множителем 2x. Бесплатные игры не приносят дополнительных бесплатных игр.
Вы не указали количество выборов или таблицу выплат, поэтому давайте в качестве примера воспользуемся таблицей выплат Pick-8 3-10-56-180-1000. Сначала рассчитаем выигрыш.
Количество способов выбить x шаров из y в кено равно количеству способов выбить x шаров из 20 и yx из 60. Это равно combin(20,x)*combin(60,yx), если выразить это в терминах Excel. Напомним, что combin(x,y) = x!/(y!*(xy)!). И наконец, x! = 1*2*3*...*x.
После этого обзора, вот таблица выплат. В правом столбце указана ожидаемая сумма выигрыша, которая нам понадобится позже.
Pick 8 Keno
| Событие | Платит | Комбинации | Вероятность | Возвращаться | Возврат^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2 558 620 845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7 724 138 400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9 512 133 400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2 362 591 575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4 651 200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| Общий | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
Далее рассчитаем средний бонус. Из приведенной выше таблицы видно, что средний выигрыш, без учета бонуса, составляет 0,593301. В рамках бонуса игрок получает 12 удвоенных бесплатных вращений. Таким образом, ожидаемый выигрыш от бонуса составляет 2×12×0,593301 = 14,239212.
Далее рассчитаем вероятность выигрыша бонуса. Если игрок поймал четыре числа, вероятность того, что 20-й шар окажется одним из этих четырех, составляет 4/20. В общем случае, если игрок поймал число c, то вероятность того, что 20-й шар способствовал выигрышу, составляет c/20.
Формула для выигрыша бонуса: вероятность(поймать 4)*(4/20) + вероятность(поймать 5)*(5/20) + вероятность(поймать 6)*(6/20) + вероятность(поймать 7)*(7/20) + вероятность(поймать 8)*(8/20). Вероятность любого выигрыша известна из приведенной выше таблицы выплат. Таким образом, вероятность выигрыша бонуса составляет:
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644.
Используя вероятность выигрыша бонуса и средний выигрыш по бонусу, мы можем рассчитать доход от бонуса как 0,021644 × 14,239212 = 0,308198.
Нам это и не нужно знать, но общая прибыль от игры равна прибыли от основной игры плюс прибыль от бонуса, что равно 0,593301 + 0,308198 = 0,901498.
Теперь давайте перейдем к рассмотрению собственно дисперсии. Напомним, что общая формула для расчета дисперсии выглядит следующим образом:
var(x + y) = var(x) + var(y) + 2*cov(x,y), где var обозначает дисперсию, а cov — ковариацию. В случае этой игры:
Общая дисперсия = дисперсия (базовая игра) + дисперсия (бонус) + 2*коэффициент покрытия (базовая игра и бонус).
Основная формула для дисперсии — E(x^2) - [E(x)]^2. Другими словами, это квадрат ожидаемой прибыли за вычетом квадрата ожидаемой прибыли.
Итак, начнём с дисперсии базовой игры. Помните, я говорил раньше, что нам понадобится квадрат ожидаемой прибыли из первой таблицы? В нижней правой ячейке первой таблицы показано, что квадрат ожидаемой прибыли равен 19,530214. Мы уже знаем, что ожидаемая прибыль составляет 0,593301. Таким образом, дисперсия базовой игры равна 19,530214 - 0,593301² = 19,178208.
Далее рассчитаем дисперсию бонуса (предполагая, что он уже был получен). Для этого вспомним, что:
var(ax) = a 2 x, где a — константа.
Также напомним, что дисперсия n случайных величин x равна nx.
При этом, если x — это базовый выигрыш в бонусной игре, то дисперсия всего бонуса составляет 2 2 × 12 × x. Из вышеизложенного мы знаем, что дисперсия одного вращения в базовой игре, не считая бонуса, равна 19,178208. Таким образом, дисперсия бонуса, при условии, что бонус уже был получен, составляет 2 2 × 12 × 19,178208 = 920,554000.
Однако нам нужно знать дисперсию бонуса до вытягивания первого шара, включая вероятность того, что бонус вообще не будет выигран. Нет, мы не можем просто умножить дисперсию бонуса на вероятность его выигрыша. Вместо этого вспомним, что var(x) = E(x^2) - [E(x)]^2. Давайте переформулируем это следующим образом:
E(x^2) = var(x) + [E(x)]^2
Нам известны среднее значение и дисперсия бонуса, поэтому квадрат ожидаемого выигрыша в бонусе составляет 920,554000 + 19,178208² = 1123,309169.
Таким образом, ожидаемый квадрат выигрыша от бонуса до вытягивания первого шара равен prob(bonus) × E(x^2) = 0,021644 × 1123,309169 = 24,313239.
Мы уже рассчитали ожидаемый выигрыш от бонуса до первого броска шара, он составляет 0,308198. Таким образом, общая дисперсия бонуса до первого броска шара составляет 24,313239 - 0,308198² = 24,218253 .
Следующий шаг — вычисление ковариации. «Почему существует корреляция между базовым выигрышем и бонусным выигрышем?», — можете спросить вы. Это потому, что последний вытянутый шар должен внести вклад в выигрыш, чтобы активировать бонус. Учитывая, что последний шар внес вклад в выигрыш, средний выигрыш увеличивается. Напомним, что формула Байеса для вероятности условия гласит:
P(A при условии B) = P(A и B)/P(B).
Давайте тогда переделаем нашу таблицу возвратов для основной игры, учитывая, что последний мяч был отбит:
В игре Pick 8 Keno последний выпавший шар считается выпавшим.
| Событие | Платит | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1 627 920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| Общий | 627,414,903 | 1.000000 | 6.757734 |
В нижней правой ячейке показано, что, если предположить, что последний мяч был отбит, средний выигрыш составляет 6,757734.
Далее, вспомните из курса статистики, который вы изучали в колледже:
cov(x,y) = exp(xy) - exp(x)*exp(y) .
В нашем случае пусть x = выигрыш в базовой игре, а y = выигрыш в бонусной игре. Давайте сначала поработаем над exp(xy).
Exp(xy) = prob(выигранный бонус)*(средняя победа в базовой игре при выигранном бонусе)*средняя победа с бонусом) + prob(невыигранный бонус)*(средняя победа в базовой игре при невыигранном бонусе)*средняя победа с бонусом при невыигранном бонусе). Легко сказать, что средняя победа с бонусом при невыигранном бонусе = 0, поэтому мы можем переписать это так:
Exp(xy) = prob(выигрыш бонуса)*(средний выигрыш в базовой игре с учетом выигранного бонуса)*средний выигрыш бонуса) =
0,021644 × 6,757734 × 14,239212 = 2,082719.Мы уже нашли E(x) и E(y), поэтому ковариация выглядит следующим образом:
cov(x,y) = exp(xy) – exp(x)*exp(y) = 2,082719 – 0,593301 × 0,308198 = 1,899865.
Вернемся к общему уравнению для дисперсии с учетом ковариации:
Общая дисперсия = дисперсия (базовая игра) + дисперсия (бонус) + 2 * ковариация (базовая игра и бонус) = 19,178208 + 24,218253 + 2 × 1,899865 = 47,196191. Стандартное отклонение равно квадратному корню из этого значения, что составляет 6,869948.
Вот и всё. На это у меня ушло несколько часов, так что надеюсь, вам понравится.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Я слышал, что вероятность развода в браке, обычно оцениваемая в 50% в США, рассчитывается как отношение числа разводов к числу браков за тот же период времени. Это правда? Считаете ли вы, что это справедливый способ расчета статистики? Я сомневаюсь, потому что вы рассматриваете разводы за короткий период времени по сравнению с браками, заключенными за длительный период.
Если бы численность населения и возрастное распределение были стабильными, то при условии, что вероятность развода действительно составляла 50%, то при большом размере выборки мы ожидали бы увидеть соотношение одного развода к двум бракам в любой заданный период времени.
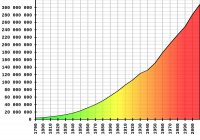
Однако численность населения нестабильна. Судя по этому графику, население США растет на 10,71% за десятилетие. Это составляет 1,02% в год. Давайте для простоты примем за 1%.
Источник карты: Бюро переписи населения США.
Согласно данным сайта fatherly.com , средняя продолжительность неудачного брака составляет 8 лет.
Если в настоящее время соотношение разводов и браков составляет 1 к 2, какова будет средняя вероятность того, что любой данный брак закончится разводом?
Сейчас мы наблюдаем разводы среди супругов, состоявших в браке 8 лет назад, когда численность населения составляла 92,35% от нынешней. Простые расчеты показывают, что реальная вероятность развода составляет 54,14%.
Давайте это проверим.
Во-первых, по данным CDC, на 1000 человек населения приходится 6,9 браков в год. Эта цифра не имеет отношения к рассматриваемому вопросу, но, я думаю, помогает понять масштаб проблемы.
Предположим, что 8 лет назад население составляло 300 000 000 человек. Это означало бы 0,69% * 300 миллионов = 2 070 000 браков в том году.
Если через восемь лет 54,14% из них заканчиваются разводом, то в настоящее время мы будем наблюдать 2 070 000 * 54,14% = 1 120 698 разводов.
1 120 698 / 2 070 000 = 50% наблюдаемое соотношение разводов к бракам в настоящее время.
Чтобы никто не сказал обратного, да, я знаю, что не все разводы заканчиваются ровно через восемь лет. Однако, учитывая все обстоятельства, я считаю, что итоговый показатель разводов будет не сильно отличаться от моего реального показателя в 54,14%.
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
В вашем офисе, где работают 100 сотрудников, проводится обмен подарками в рамках игры «Тайный Санта». Для этого нужно написать имена всех участников на отдельных листочках бумаги, положить их в шляпу, и каждый случайным образом вытягивает имя, которому дарит подарок.
Вопрос в том, сколько в среднем будет замкнутых циклов? Например, в одном замкнутом цикле Гордон дает деньги Дону, тот дает деньги Джону, тот дает деньги Натану, тот дает деньги Гордону. Или вот пример розыгрыша собственного имени.
Предположим, каждый выбирает по одному варианту за раз. В процессе выбора каждого участника будут возникать две ситуации:
- Имя того, кто выбирает, уже выбрано.
- Имя того, кто выбирает, всё ещё находится в списке имён.
Допустим, для любого выбранного участника осталось n человек, которым нужно выбрать.
Если имя того, кто выбирает, уже выбрано, существует вероятность 1/n, что он выберет имя, замыкая цикл, связанный с его именем. Например, предположим, что Эми выбирает. Имя Эми уже занято Бобом, имя Боба уже занято Чарли, а имя Чарли все еще находится в корзине. При наличии n имен в корзине существует вероятность 1/n, что Эми выберет имя Чарли, замыкая цикл.
Если имя того, кто выбирает, еще не выбрано, существует вероятность 1/n, что Эми выберет свое собственное имя, замкнув цикл.
В любом случае, если сборщик не замыкает цепочку, он присоединяется к части другой цепочки, которая в конечном итоге будет замкнута кем-то другим. Каждую цепочку следует учитывать только один раз, когда она замыкается.
Таким образом, ответ равен 1/100 + 1/99 + 1/98 + ... + 1/1 ≈ 5,187377518.
Для любого достаточно большого числа игроков n оценка равна ln(n).
Этот вопрос задаётся и обсуждается на моём форуме Wizard of Vegas .
Какова будет стоимость дополнительного гарантированного дикого символа при игре в видеослот?
Это зависит от многих факторов. Я бы истолковал ваш вопрос так: какова ценность дополнительного дикого символа сверх среднего количества, которое игрок обычно получает? Хотя ответ будет значительно варьироваться от игры к игре, важным фактором является количество рядов на экране. Если рядов три, дополнительный дикий символ принесет пользу 1/3 линий выплат. Аналогично, если рядов четыре, его ценность будет ниже, он повлияет на 1/4 линий выплат.
Чтобы ответить на ваш вопрос, я рассмотрел игру «Клеопатра» , которую я уже проанализировал. В следующей таблице показано увеличение ожидаемого значения для дикого символа по сравнению со случайным количеством диких символов.
Ценность сорта Extra Wild в Клеопатре
| Кисть | 3 ряда | 4 ряда |
|---|---|---|
| 1 | 95,71% | 71,79% |
| 2 | 99,76% | 74,82% |
| 3 | 76,24% | 57,18% |
| 4 | 21,25% | 15,93% |
| 5 | 1,96% | 1,47% |