WOO logo

Wizard рекомендует

Спросите Волшебника #321

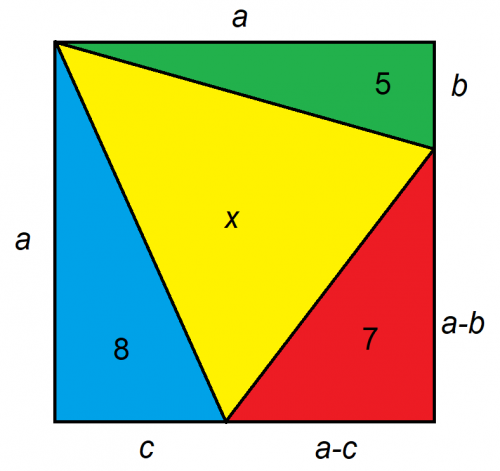
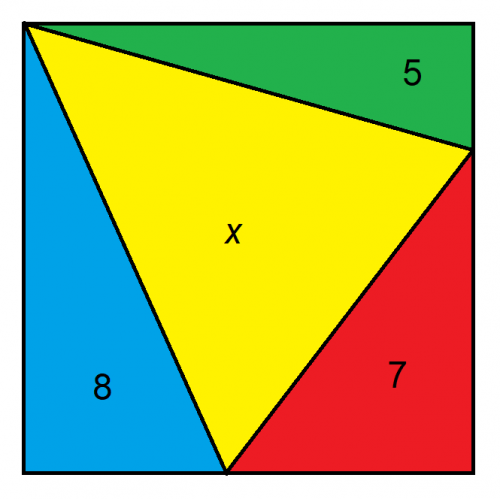
Учитывая, что большая фигура представляет собой квадрат, чему равна площадь x?

Dyana от Las Vegas

Ключ к решению подобных задач — в их формулировке. Я рекомендую свести задачу к как можно меньшему числу неизвестных. В данном случае мы можем выразить неизвестные расстояния на квадрате всего тремя следующим образом:

решение в виде четырех треугольников в квадрате

С прямоугольниками работать проще, чем с треугольниками. Зная площадь трёх треугольников, мы можем удвоить их размер и площадь. Это даёт нам:

  • ab=10
  • ac=16
  • (ab)(ac)=14

Разложим (ab)(ac) на множители:

a 2 - ab- ac + bc = 14

a 2 - 10 - 16 + bc = 14

(1) a 2 + bc = 40

Давайте выразим b и c через a, чтобы свести все к одной переменной:

b = 10/a

c = 16/a

Подставляя эти значения для b и c в уравнение (1):

a² + (10/a)*(16/a) = 40

a² + 160/ a² = 18

Далее, избавимся от двойки в знаменателе, умножив всё на 2 .

a 4 + 160 = 40*a 2

a 4 - 40*a 2 + 160 = 0

Давайте определим новую переменную y = a²

y² - 18y + 32 = 0

Далее, решим уравнение относительно y, используя формулу квадратного уравнения:

y = (40 +/- sqrt(1600-640))/2

y = (40 +/- sqrt(960))/2

y = (40 +/- 8*sqrt(15))/2

y = 20 +/- 4*sqrt(15)

Площадь всего квадрата равна a² , что удобно равно y. Из приведенного выше уравнения, если +/- отрицательно, то y = приблизительно 4,5081, что, очевидно, неверно, поскольку мы знаем, что площадь составляет не менее 20, даже не считая x. Следовательно, площадь квадрата должна быть равна 20 + 4 * sqrt(15).

Площадь трех данных нам треугольников равна 5+7+8=20. Вычитая это значение из общей площади квадрата, получаем площадь x: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = приблизительно 15,4919.

Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .

Санкост

Обратите внимание на мою футболку на этом снимке. Кассирша в кинотеатре похвалила её, когда я ходила смотреть «Неограненные алмазы» . В благодарность я замучила её этой задачей, только с треугольниками с площадями 2, 3 и 4. После фильма я подошла к ней, чтобы узнать, как она, и она всё ещё не решила задачу, но, казалось, пыталась. Поэтому я записала для неё следующее решение в баре «Санкост». Ей, кажется, это даже понравилось. Думаю, эта молодая женщина многого добьётся в жизни.

Что касается лотереи, существует ли в многоштатных лотереях (Powerball, Mega Millions) «критическая точка» размера джекпота, после которой вероятность того, что главный приз будет разделен между двумя победителями, выше, чем вероятность того, что победитель будет один? Если да, то какова эта величина?

Ayecarumba от California

Я не буду вдаваться в математические расчеты, но вот точки, где вероятность выигрыша нескольких победителей примерно равна вероятности выигрыша одного:

  • PowerBall: 975 миллионов долларов
  • Mega Millions: 1,65 миллиарда долларов

Вы, конечно, не спрашивали, но вот джекпоты, где вероятность выигрыша хотя бы одного победителя равна вероятности того, что ни одного не будет (50%).

  • PowerBall: 704 миллиона долларов
  • Mega Millions: 867 миллионов долларов

Этот вопрос обсуждался на моём форуме, посвящённом игре Wizard of Vegas .

  • В тюрьме находятся 12 заключенных, каждый из которых пронумерован от 1 до 12.
  • Начальник тюрьмы устанавливает 12 ящиков, каждый из которых пронумерован от 1 до 12.
  • Внутри 12 коробочек случайным образом расположены числа от 1 до 12, по одному в каждой коробочке.
  • Каждому заключенному разрешается по очереди открыть шесть ящиков по своему выбору. Он может выбирать и открывать их по одному.
  • Цель каждого заключенного — найти свой номер внутри коробки среди шести предложенных вариантов. Если ему это удается, считается, что этот человек выжил.
  • Если заключенный не найдет свой номер, то вся группа считается провалившей задание, и их немедленно отправят на расстрел.
  • Если заключенный выживает, то он должен вернуть номера в исходные ячейки для следующего заключенного.
  • После начала игры заключенным запрещается наблюдать за другими игроками или общаться с ними.
  • Перед началом всей группе разрешается совместно разработать стратегию. Цель состоит в том, чтобы все 12 заключенных выжили (другими словами, нашли свой номер внутри коробки).

Какова должна быть их стратегия, чтобы максимизировать вероятность выживания, и какова эта вероятность?

анонимный

Следуя стратегии, описанной в решении, вероятность выживания составляет 166112640/479001600 = приблизительно 34,68%.

Первым делом каждый заключенный должен выбрать свой тюремный номер. Если это номер, то он выживает. Если нет, то он открывает ящик с номером внутри первого ящика. Он повторяет этот процесс, пока не откроет шесть ящиков или не найдет свой номер.

Подобно игре «Тайный Санта», здесь будут петли, ведущие от одного числа к другому. При наличии 12 заключенных может быть от 1 до 12 петель. Если ни одна петля не длиннее шести, то каждый заключенный в конце концов найдет свое число. Главный вопрос: какова вероятность того, что ни одна петля не будет длиннее шести? Давайте рассмотрим обратную ситуацию и найдем количество комбинаций петель длиной 7 или более.

Решение 12-го заключённого

Циклы Комбинации Вероятность
12 39 916 800 0.083333
11,1 43 545 600 0.090909
10,2 23 950 080 0.050000
10,1,1 23 950 080 0.050000
9,3 17 740 800 0.037037
9,2,1 26 611 200 0.055556
9,1,1,1 8 870 400 0.018519
8,4 14 968 800 0.031250
8,3,1 19 958 400 0.041667
8,2,2 7 484 400 0.015625
8,2,1,1 14 968 800 0.031250
8,1,1,1,1 2 494 800 0.005208
7,5 13 685 760 0.028571
7,4,1 17,107,200 0.035714
7,3,2 11 404 800 0.023810
7,3,1,1 11 404 800 0.023810
7,2,2,1 8 553 600 0.017857
7,2,1,1,1 5 702 400 0.011905
7,1,1,1,1,1 570,240 0.001190
Общий 312,888,960 0.653211

В следующей таблице приведены формулы для комбинаций, представленных в таблице выше.

Комбинированные формулы

Циклы Комбинации Формула
12 39916800 =ФАКТ(11)
11,1 43545600 =COMBIN(12,11)*FACT(10)
10,2 23950080 =COMBIN(12,10)*FACT(9)
10,1,1 23950080 =COMBIN(12,10)*FACT(9)
9,3 17740800 =COMBIN(12,9)*FACT(8)*FACT(2)
9,2,1 26611200 =КОМБИН(12,9)*КОМБИН(3,2)*ФАКТ(8)
9,1,1,1 8870400 =COMBIN(12,9)*FACT(8)
8,4 14968800 =COMBIN(12,8)*FACT(7)*FACT(3)
8,3,1 19958400 =КОМБИН(12,8)*КОМБИН(4,3)*ФАКТ(7)*ФАКТ(2)
8,2,2 7484400 =КОМБИН(12,8)*КОМБИН(4,2)*ФАКТ(7)/2
8,2,1,1 14968800 =КОМБИН(12,8)*КОМБИН(4,2)*ФАКТ(7)
8,1,1,1,1 2494800 =COMBIN(12,8)*FACT(7)
7,5 13685760 =COMBIN(12,7)*FACT(6)*FACT(4)
7,4,1 17107200 =COMBIN(12,7)*5*FACT(6)*FACT(3)
7,3,2 11404800 =КОМБИН(12,7)*КОМБИН(5,3)*ФАКТ(6)*ФАКТ(2)
7,3,1,1 11404800 =КОМБИН(12,7)*КОМБИН(5,3)*ФАКТ(6)*ФАКТ(2)
7,2,2,1 8553600 =КОМБИН(12,7)*КОМБИН(5,2)*КОМБИН(3,2)*ФАКТ(6)/2
7,2,1,1,1 5702400 =КОМБИН(12,7)*КОМБИН(5,2)*ФАКТ(6)
7,1,1,1,1,1 570240 =COMBIN(12,7)*FACT(6)

В нижней правой ячейке первой таблицы содержится 312 888 960 проигрышных комбинаций. Общее количество способов расположения чисел равно 12! = 479 001 600. Таким образом, вероятность неудачи составляет 312 888 960 / 479 001 600 = 65,32%. Следовательно, вероятность успеха составляет 100% - 65,32% = 34,68%.

Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .

Здравствуйте. У меня есть купон, позволяющий мне собрать комбинацию из 22 очков. Я могу сохранить купон до тех пор, пока не соберу свои первые 22 очка. Он не распространяется на удвоения или разделения. Какова его стоимость?

MrGoldenSun

Быстрый ответ — это максимальная разрешенная ставка. Просто дождитесь выпадения 22 и сделайте ставку, в результате чего уйдете из-за стола с дополнительной единицей.

Более объективный ответ должен учитывать стоимость ожидания этих 22 очков. Точно это мне неизвестно, но я могу оценить.

Для игрока правило «дилер набирает 22 очка» обходится в 6,91%. Однако дилер наберет 22 очка чаще, чем указано, поскольку игроку будет все равно, если он первым превысит лимит. В зависимости от правил, игрок превысит лимит примерно в 15,7% случаев. Если предположить, что это не коррелирует с вероятностью превышения лимита дилером (что не так), то вероятность превышения лимита дилером составляет 6,91%/(1,0-0,157) = 8,2%.

Я понимаю, это приблизительный расчет, но давайте предположим, что вероятность выпадения 22 у игрока одинакова. Я знаю, что дилер чаще проигрывает, чем игрок, но этот купон также не учитывается после разделения, поэтому давайте просто предположим, что эти факторы компенсируют друг друга. Таким образом, если игрок получает 22 в 8,2% раздач, то в среднем он будет получать 22 примерно каждые 1/0,082 = 12,2 раздачи.

Допустим, преимущество казино в базовой игре составляет 0,75%. Стоимость игры 12,2 раздач при таком преимуществе казино составляет 12,2 * 0,0075 = 0,0915. Вычтем это из стоимости одной единицы, и получим стоимость купона 1,0 - 0,0915, что составляет примерно 91% от номинальной стоимости.

Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .