Спросите Волшебника #322
Я сел за стол, чтобы сыграть в техасский холдем, и в раздаче у меня оказался стрит-флеш. Двое других игроков за столом заметили, что это уже третий флеш подряд. Какова вероятность такого совпадения?
В игре в техасский холдем с участием 10 игроков, при условии, что никто никогда не сбрасывает карты, вероятность того, что старшая комбинация будет стритом или роял-флешем, составляет 1 к 350,14. Вероятность того, что это произойдет три раза из трех, составляет 1 к 42 926 491.
Однако игра за этим столом могла продолжаться несколько часов. Возможно, более реалистичный вопрос — какова вероятность того, что это произойдет хотя бы раз за весь день? Предполагая, что игра длится 24 часа и совершается 24 раздачи в час, ответ на этот вопрос будет 1 к 59 621.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Предположим, вы выбрали правильную стратегию. Какова вероятность выигрыша при рейзе в 4 раза в Ultimate Texas Hold 'Em? Я зафиксировал 96 раздач с рейзом в 4 раза. Не считая пушей, у меня было 66 побед и 30 поражений. Как это соотносится с ожиданиями?
При условии правильной стратегии повышения ставки в 4 раза, существует вероятность каждого исхода при повышении ставки в 4 раза:
- Победа: 58,82%
- Убыток: 38,47%
- Ничья: 2,72%
Если исключить ничьи, вероятность выигрыша составит 60,46%. Из 96 разыгранных раздач ожидаемое количество выигрышей с 4-кратным увеличением составляет 58,04. Таким образом, 66 выигрышей опережают ожидания, но ненамного.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
У Акселя и Боба есть свои колоды по 52 карты. Оба перемешивают их случайным образом. Затем они одновременно переворачивают по одной карте из каждой колоды. Какова вероятность того, что они хотя бы раз перевернут одну и ту же карту одновременно?
Ответ можно было бы легко оценить как 1-(51/52) 52 = 0,63568648. Однако приблизительные оценки настолько неудовлетворительны с интеллектуальной точки зрения. Поэтому давайте найдем точное решение!
Шаг 1: Для начала рассмотрим количество способов упорядочить вторую колоду, чтобы первая карта была номером 1. Ответ — это количество способов упорядочить остальные 51 карты, которое равно 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Любая карта может совпадать с первой колодой, поэтому мы должны сделать это для всех 52 карт. Это даст нам 52*51! = 52! комбинаций, в которых совпадает хотя бы одна карта.
Шаг 2: Однако на шаге 1 дважды учитывается каждая ситуация, когда две карты совпадают. Например, если первыми двумя картами были 1 и 2, мы бы дважды посчитали 50! способов расположить остальные карты: один раз для 1 в качестве первой карты и второй раз для 2 в качестве второй карты. Количество способов выбрать 2 карты из 52 равно combin(52,2) = 1326. Для каждой комбинации из двух карт существует 50! = 30414093201713378043612608166064768844377641568960512000000000000 способов расположить остальные карты. Таким образом, на шаге 2 нам нужно вычесть combin(52,2)*50! = (52*51/2!)*50! = 52!/2! комбинаций.
Шаг 3: Далее рассмотрим ситуацию, когда первые три карты в случайной колоде имеют последовательность 1, 2 и 3. Существует 49! способов упорядочить остальные 49 карт. На начальном этапе, когда подсчитывалась хотя бы одна совпадающая карта, мы бы посчитали их три раза. Затем на втором этапе мы бы вычли все комбинации (3,2) = 3 способа выбрать 2 из этих трех карт. Таким образом, эта ситуация была бы учтена 3-3 = 0 раз, поэтому нам нужно добавить их обратно. Существует комбинаций (52,3) таких ситуаций, когда выбираются хотя бы 3 совпадающие карты. Поэтому нам нужно добавить обратно комбинации (52,3) * 49! = 52 * 51 * 50 * 49! / 3! = 52! / 3!.
Шаг 4: Далее рассмотрим ситуацию, когда первые четыре карты в случайной колоде — это 1, 2, 3 и 4 в порядке следования. Существует 48! способов упорядочить остальные 48 карт. На начальном этапе подсчета хотя бы одной совпадающей карты мы бы посчитали их четыре раза. Затем на шаге 2 мы бы вычли все комбинации (4,2) = 6 способов выбрать две из этих четырех карт. Затем мы бы добавили все комбинации (4,3) = 4 способа выбрать три из этих четырех карт. Таким образом, мы получаем 4-6+4=2 способа, которые были бы учтены для каждой такой ситуации. Поэтому нам нужно вычесть один из этих способов, чтобы каждая ситуация была учтена один раз. Существует комбинаций (52,4)*48! = 52*51*50*49*48!/4! = 52!/4! таких ситуаций, которые необходимо добавить обратно.
Мы будем продолжать это делать, чередуя сложение и вычитание, чтобы исправить двойной подсчет.
В итоге, количество ситуаций, когда хотя бы одна карта в случайной колоде совпадает с упорядоченной колодой, равно: combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
Всего существует 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 способов упорядочить 52 карты.
Таким образом, ответ: x/y = 0,6321205588285576784044762298
Вероятность отсутствия совпадений составляет 1-(x/y) = 0,3678794411714423215955237702.
Если это число кажется вам знакомым, так и должно быть. 1/e = 0,3678794411714423215955237702.
Таким образом, ответ можно с ОЧЕНЬ высокой точностью оценить как 1-(1/e).
Благодарности
Математические расчеты проводились в парижском/гальваническом пространстве.
Эта проблема была задана и обсуждалась на моём форуме в Wizard of Vegas .
В документе под названием « Вероятности комбинаций в бинго» (PDF), размещенном на вашем сайте, вы указываете следующее ожидаемое количество вызовов для определения победителя при наличии 300 игровых карт:
- Четыре угла: 8.43
- Маленький бриллиант: 11,833
В обоих случаях достаточно всего четырех отметок, и для победы есть только один способ. Почему же ожидаемое количество шаров для определения победителя различается?
На этот вопрос сложно ответить однозначно. Начну с того, что ожидаемое количество звонков в игре с одной картой будет одинаковым. Однако существует корреляционный эффект при игре с несколькими картами.
На этот вопрос сложно дать однозначный ответ, но если уж совсем придираться, то причина в том, что для четырехугольной схемы требуется концентрация шаров в столбцах B и O. В схеме с маленьким ромбом вероятность попадания выше при более равномерном распределении шаров по столбцам B, N и O.
Давайте упростим игру до варианта, где в игре бесконечное количество карт, а шары вытягиваются с заменой. Вот количество шаров, необходимых для определения победителя в обеих играх:
- Четыре угла: 2,5 + 2,5 + ((1/2) * 10 + (1/2) * (2,5 + 5)) = 13,75
- Маленький ромб: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
Это показывает, что в четыре угла помещается на 1,53 мяча больше.
Проведя симуляцию по обычным правилам бинго, предполагая бесконечное количество карточек, получаем следующие результаты:
- Четыре угла: 12.8289
- Алмаз: 11,3645
На этот раз другое количество мячей – 1,46.
Я надеюсь показать, что закономерности быстрее заполняются, если отметки распределены по большему количеству столбцов. Поэтому я думаю, что в одной игре в бинго обычно выигрышная комбинация — горизонтальная.
Этот вопрос обсуждался на моём форуме, посвящённом игре Wizard of Vegas .
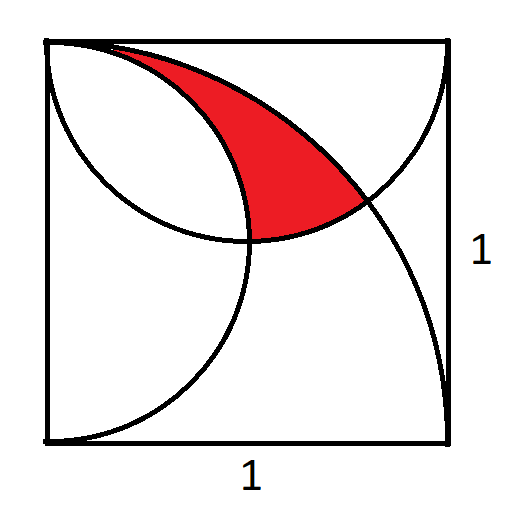
На рисунке выше изображена четверть окружности и две полуокружности внутри квадрата со стороной длиной один. Вопрос: какова площадь красной области?
Нажмите на следующую кнопку, чтобы увидеть мой ответ.
Нажмите на следующую кнопку, чтобы увидеть моё решение.
Вот ссылка на мое решение . (PDF)
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Благодарности: Я хотел бы поблагодарить Mind Your Decisions за эту математическую головоломку.


