Спросите Волшебника #323
Насколько хороша эта экспресс-карта?

На первом этапе вам нужно сделать ставку в любую сторону против форы в игре НФЛ. На момент, когда вы задали этот вопрос (2 января 2020 г.), «Викинги» считались аутсайдерами с форой в 7,5 очков. Согласно моему калькулятору альтернативных ставок на НФЛ , вероятность победы «Викингов» с форой +8,5 составляет 52,22%.
Для всех остальных игр я анализировал коэффициенты ставок, вычитал маржу и рассчитывал вероятность выигрыша. В следующей таблице показана вероятность выигрыша в каждом из этапов.
Карта экспресс-ставки William Hill
| Нога | Справедливое вино | Вероятная победа |
|---|---|---|
| Святые -8,5 | -7.5 | 47,78% |
| Викинги +8.5 | 8.5 | 52,22% |
| Хоу | -135 | 57,45% |
| Счета | 135 | 42,55% |
| Патриоты | -205 | 67,21% |
| Титаны | 205 | 32,79% |
| Море | -118 | 54,13% |
| Фил | 118 | 45,87% |
| ЛСУ | -200 | 66,67% |
| Клемсон | 200 | 33,33% |
| АФК | -130 | 56,52% |
| НФК | 130 | 43,48% |
На первом этапе у двух команд с наибольшими шансами на победу — «Патриоты» и «ЛСУ». Вот вероятность победы моих рекомендованных команд:
- Викинги +8,5 — 52,22%
- Патриоты — 67,21%
- LSU — 66,67%
Произведение этих вероятностей составляет 23,40%. Получение 4 выигрышей по цене 1 дает доходность 4 × 23,40% = 93,60%. Другими словами, преимущество казино составляет 6,40%. Поэтому я бы не стал в это ввязываться.
Я подумываю о создании дополнительной ставки для вариантов блэкджека "ничья 22", которая будет выплачиваться 11 к 1, если дилер превысит 22 очка. Каковы будут шансы?
Я подумываю о создании дополнительной ставки для вариантов блэкджека "ничья 22", которая будет выигрывать, если дилер превысит 22 очка. Каков должен быть коэффициент выигрыша и каково будет преимущество казино?
Предположим, дилер всегда брал карты (даже если все игроки уже перебрали). Тогда я показываю вероятность перебора при 22 в 7,88%, если дилер останавливается на мягкой 17, и 8,00%, если он берет карту при мягкой 17.
Предположим, дилер берет карту, имея «мягкие» 17. При выигрыше 11 к 1 преимущество казино составит 4,04%. При 10 к 1 оно подскочит до 12,04%.
Я должен предупредить вас и сообщить игрокам, что это будет засчитано (заткнись, Виз!).
Эми и Боб устраивают соревнование: кто первым выиграет четыре подбрасывания честной монеты. Эми хочет поставить 8000 долларов на свою победу. Однако она может делать ставки только на одно подбрасывание за раз. Все ставки выплачиваются с равными шансами. Как ей составить свои ставки так, чтобы выиграть 8000 долларов, если она выиграет всю серию, и проиграть 8000 долларов, если выиграет Боб?
Нажмите на кнопку ниже, чтобы увидеть ответ.
[спойлер=Ответ]В середине серии может быть 16 возможных состояний. В следующей таблице показана ставка, которую Эми должна сделать в каждом из них, и ее баланс до совершения ставки, следуя этой стратегии.
Отвечать
| Эми | Боб | Баланс | Ставка |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
Нажмите на кнопку ниже, чтобы получить решение.
[spoiler=Решение]Позволять:
- а = Эми побеждает
- b = Боб побеждает
- w = чистая победа Эми в серии на данный момент
- f(a,b,w) = размер ставки Эми в следующей игре
В подобных головоломках обычно хорошей стратегией является начало и конец, а затем движение к началу. При этом легко заметить, что:
f(3,3,0) = 8000
В этой ситуации 7-я игра — «победитель забирает всё». У Эми должен быть нулевой выигрыш, и она ставит 8000 на последний бросок, что принесёт ей 8000 выигрыша в случае победы и 8000 проигрыша в противном случае.
Вернемся на шаг назад. Что если у нее 3 выигрыша, а у Боба 2? Если она выиграет следующий бросок, она выиграет всю игру. Если проиграет, счет будет 3-3. Исходя из f(3,3,0), у нее должно быть 0, если счет 3,3. Таким образом, нам нужно, чтобы у нее было 8000, если она выиграет следующий бросок, и 0 в противном случае. В итоге мы получим чистый выигрыш в районе 4000 и ставку в той же сумме. Итак:
f(3,2,4000)=4000
Вернемся на шаг назад. Что если у нее 3 победы, а у Боба 1? Если она выиграет следующий ход, она выиграет всю игру. Если проиграет, счет будет 3-2. Исходя из f(3,2,4000), у нее должно быть 4000, если счет 3,2. Таким образом, ей нужно иметь 8000, если она выиграет следующий ход, и 4000 в противном случае. В итоге мы получим чистый выигрыш в середине [(4000+8000)/2=6000] и ставку в размере половины расстояния между этими двумя целями, [(8000-4000)/2 = 2000]. Итак:
f(3,1,6000) = 2000
Вернемся на шаг назад. Что если у нее 3 победы, а у Боба 0? Если она выиграет следующий ход, она выиграет всю игру. Если проиграет, счет будет 3-1. Исходя из f(3,1,6000), у нее должно быть 6000, если счет 3,1. Таким образом, ей нужно иметь 8000, если она выиграет следующий ход, и 6000 в противном случае. В итоге мы получим чистый выигрыш в середине [(6000+8000)/2=7000] и ставку в размере половины расстояния между этими двумя целями, [(8000-4000)/2 = 2000]. Итак:
f(3,0,7000) = 1000
Надеюсь, очевидно, что в случае ничьей у Эми должен быть нулевой чистый выигрыш. В любом случае, вероятность её победы в серии составит 50%. При сбалансированных целях в 8000 очков в любом случае, ей нужно ставить 0, иначе у неё будет шанс не достичь ни одной из целей.
Далее, если Эми когда-либо окажется в отставании в серии, её чистый выигрыш должен быть -1, умноженный на чистый выигрыш, если бы она лидировала с тем же счётом. Например, рассмотрим счёт Эми 2 - Боб 3 (или 2-3). Если она проиграет следующий бросок, она проиграет всю игру. Если она выиграет, её счёт будет 3-3. Из f(3,3,0) мы видим, что у неё должно быть 0, если счёт 3,3. Таким образом, нам нужно, чтобы у неё было 0, если она выиграет следующий бросок, и -8000 в противном случае. В результате чистый убыток составит около 4000, а ставка — ту же сумму. Итак:
f(2,3,-4000)=4000
По той же логике:
f(1,3,-6000) = 2000
f(0,3,-7000) = 1000
Далее, какую ставку должна сделать Эми, если счет 2-2? Если она выиграет, счет будет 3-2. Из вышеизложенного видно, что при таком счете ее чистый выигрыш должен составить 4000. Также видно, что если она проигрывает со счетом 2-3, ее чистый убыток должен составить 4000. Таким образом, ей нужно поставить 4000:
f(2,2,0) = 4000
Вернемся на шаг назад. Что если счет будет 2-1? Мы установили, что ей нужен чистый выигрыш в 6000, если она выиграет следующий ход (счет 3-1), и чистый выигрыш в 0, если она проиграет (счет 2-2). В этом случае чистый выигрыш будет равен [(6000+0)/2=3000], а ставка составит половину расстояния между этими двумя целями, [(6000-0)/2 = 3000]. Итак:
f(2,1,3000) = 3000
Вернемся на шаг назад. Что если у нее будет 2 победы, а у Боба 0? Если она выиграет следующий ход, счет будет 3-0. Если проиграет, счет будет 2-1. При счете 3-0 ее чистый выигрыш должен составить 7000, а при 2-1 — 3000. При счете 2-0 чистый выигрыш составит [(7000+3000)/2=5000], а ставка — половину расстояния между этими двумя целями, [(7000-3000)/2 = 2000]. Итак:
f(2,0,5000) = 2000
Поменяв местами результаты матчей, где у Алисы две победы, а у Боба меньше, мы также узнаем:
f(1,2,-3000) = 3000
f(0,2,-5000) = 2000
Как объяснялось ранее, чистый выигрыш Эми должен быть равен 0, если серия будет сбалансированной, поэтому при счете 1-1 ее чистый выигрыш должен быть равен 0. При счете 2-1 ей нужно выиграть 2000, а при 1-2 — проиграть 2000. Таким образом, при ничьей 1-1 ей следует поставить 2000, или:
f(1,1,0) = 2000
Что если Эми ведёт 1-0? Мы выяснили, что при счёте 2-0 ей нужно вести 5000. При счёте 1-1 ей нужно сравнять счёт.При счете 1-0 мы получим чистую победу по центру [(5000+0)/2=2500] и ставку в размере половины расстояния между этими двумя голами, [(5000-0)/2 = 2500]. Итак:
f(1,0,2500) = 2500
Перевернув счет на 0-1:
f(0,1,-2500) = 2500
Итак, наконец, мы подошли к первой игре со счетом 0-0. Нам нужно, чтобы Эми выиграла 2500, если выиграет следующий бросок, и проиграла 2500, если проиграет. Таким образом, ставка в 2500 позволит нам достичь этой цели. Или:
f(0,0,0) = 2500
[/спойлер]Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
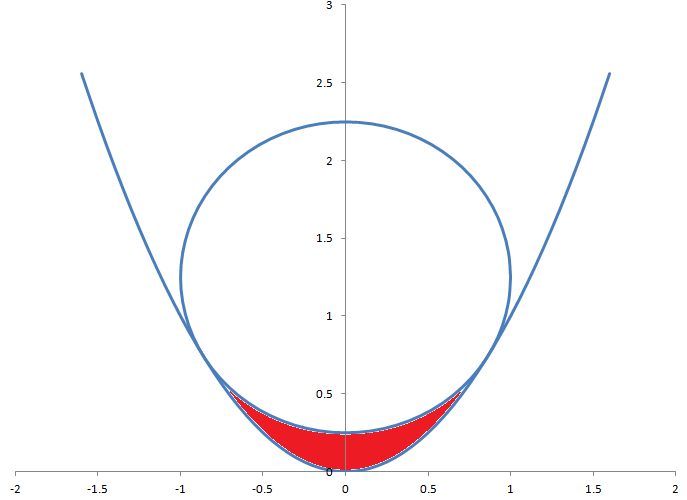
Окружность радиусом 1 касается параболы, уравнение которой задано как y= x² . Какова площадь области, выделенной красным цветом, между окружностью и параболой?
Нажмите на кнопку ниже, чтобы увидеть ответ.
Вот моё решение . (PDF)
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Эту проблему мне подсказал Преш Талвалкер из Mind Your Decisions .


