Спросите Волшебника #326
Что представляет собой стратегия «Железный крест» в игре в кости, и что вы о ней думаете?
«Железный крест» — это способ делать ставки на поле и делать ставки на выигрыш при любом броске кубиков, кроме 7. Поле уже включает 2, 3, 4, 9, 10, 11 и 12. Игрок добавляет к этому ставки на 5, 6 и 8, чтобы охватить остальные числа, кроме 7. В следующей таблице показано, как выглядит расчет при ставке на поле в 5 долларов, ставке на 5 долларов на 5 и ставках на 6 и 8 в 6 долларов.
Железный крест
| Сумма выпавших кубиков | Победить | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|---|
| 2 | 10 | 1 | 0.027778 | 0.277778 |
| 3 | 5 | 2 | 0.055556 | 0.277778 |
| 4 | 5 | 3 | 0.083333 | 0.416667 |
| 5 | 2 | 4 | 0.111111 | 0.222222 |
| 6 | 2 | 5 | 0.138889 | 0.277778 |
| 7 | -22 | 6 | 0.166667 | -3.666667 |
| 8 | 2 | 5 | 0.138889 | 0.277778 |
| 9 | 5 | 4 | 0.111111 | 0.555556 |
| 10 | 5 | 3 | 0.083333 | 0.416667 |
| 11 | 5 | 2 | 0.055556 | 0.277778 |
| 12 | 15 | 1 | 0.027778 | 0.416667 |
| 36 | 1.000000 | -0.250000 |
В нижней правой ячейке таблицы указан ожидаемый убыток в размере 0,25 доллара. Общая сумма ставок составляет 22 доллара. Таким образом, общее преимущество казино составляет 0,25/22 = 1/88 = 1,14%.
На этом этапе вы, возможно, задаетесь вопросом, почему преимущество казино может быть ниже, чем преимущество казино по каждой отдельной ставке. Ответ прост: преимущество казино в 1,52% при ставках на 6 и 8 и 4,00% при ставке на 5 рассчитывается на основе каждой завершенной ставки. Если рассматривать преимущество казино при ставках на количество выпавших чисел в расчете на один бросок, то преимущество казино при ставках на 6 или 8 составляет 0,46%, а при ставках на 5 — 1,11%.
Мы можем рассчитать преимущество казино в 1,14%, взяв средневзвешенное значение всех сделанных ставок, следующим образом:
($5*2,78% + $5*1,11% + $12*0,46%)/22 = $0,25/$22 = 1,14%.
Остерегайтесь казино, которые выплачивают только 2 к 1 за ставку на 12 очков. Настаивайте на получении полной выплаты 3 к 1. Неполная выплата удваивает преимущество казино по этой ставке с 2,78% до 5,56%.
На мой взгляд, по сравнению с большинством игр, ставка в 1,14% — это довольно неплохой результат. Однако в крэпсе можно добиться гораздо лучших результатов. Например, при коэффициентах 3-4-5x, делая ставки на «пас» и «ком» с полными коэффициентами, вы можете снизить преимущество казино до 0,37%. В обратном случае, делая ставки на «не пас» и «не ком», плюс ставя на полные коэффициенты, вы получите преимущество казино в 0,27%.Каково ожидаемое количество бросков честной игральной кости, при котором каждая грань выпадет не менее двух раз?
Хотя эту задачу можно было бы решить с помощью длинной и утомительной цепи Маркова, я предпочитаю интегральное решение. Я объясняю, как использовать этот метод, на своих страницах, посвященных игре Fire Bet и Bonus Craps .
Представьте, что вместо того, чтобы значимые события определялись броском игральной кости по одному, рассматривайте их как мгновение во времени. Предположим, что время между событиями обладает свойством отсутствия памяти, со средним временем между событиями в одну единицу времени. Другими словами, время между событиями подчиняется экспоненциальному распределению со средним значением 1. Это не будет иметь значения для целей разрешения пари, поскольку события по-прежнему происходят по одному.
Согласно распределению Пуассона, вероятность того, что любая заданная сторона игральной кости была брошена ноль раз за x единиц времени, равна exp(-x/6)*(x/6) 0 /0! = exp(-x/6). Также распределение Пуассона утверждает, что вероятность того, что любая заданная сторона была брошена ровно один раз, равна exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6). Таким образом, вероятность того, что любая сторона была брошена два или более раз за x единиц времени, равна 1 - exp(-x/6)*(1 + (x/6)). Вероятность того, что все шесть сторон были брошены хотя бы дважды, равна (1 - exp(-x/6)*(1 + (x/6))) 6. Вероятность того, что хотя бы одна сторона не была брошена хотя бы дважды, равна:
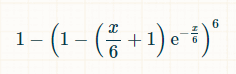
Нам необходимо интегрировать эти данные по всему времени, чтобы определить, сколько времени в среднем пройдет, прежде чем желаемая цель будет достигнута.
К счастью, на этом этапе мы можем использовать калькулятор интегралов . Для калькулятора, ссылка на который приведена ниже, введите 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 в текстовое поле после "Вычислить интеграл от" и в разделе "Пользовательский" установите границу интегрирования от 0 до ∞.
Ответ: 390968681 / 16200000 = приблизительно 24,13386919753086
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
У меня вопрос, состоящий из двух частей.
Для части 1 дано:- x + y + z = 1
- x² + y² + z² = 4
- x³ + y³ + z³ = 9
Чему равно x^4 + y^4 + z^4?
Что касается второй части вопроса, каков ответ на общий случай, когда:
- x + y + z = a
- x² + y² + z² = b
- x³ + y³ + z³ = c
Вопрос 1: 97/6 = приблизительно 16,166666
Вопрос 2: a 4 /6 + (4/3)ac - a 2 b + b 2 /2
См. мое решение (PDF)
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
Вы начинаете с честной шестигранной игральной кости и бросаете её шесть раз, записывая результаты каждого броска. Затем вы записываете эти числа на шесть граней другой, немаркированной честной игральной кости. Например, если ваши шесть бросков были 3, 5, 3, 6, 1 и 2, то на вашей второй кости не будет 4, а вместо этого будут две тройки.
Затем вы бросаете этот второй кубик шесть раз. Вы берете эти шесть чисел и записываете их на грани еще одного честного кубика, и продолжаете этот процесс создания нового кубика на основе предыдущего.
В конечном итоге у вас получится игральная кость с одинаковым числом на всех шести гранях. Каково среднее число переходов от одной кости к другой (или общее количество бросков, деленное на 6), необходимое для достижения этого состояния?
Давайте обозначим начальное состояние игральной кости буквами, а не цифрами, чтобы избежать путаницы. Давайте обозначим буквами каждое возможное состояние игральной кости. Например, AAABBC будет означать три одинаковых числа, два одинаковых числа и одно третье число. Начальное состояние, очевидно, будет ABCDEF.
Пусть E(ABCDEF) — ожидаемое количество бросков кубика из состояния ABCDEF.
E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656Исходя из количества комбинаций перехода из одного состояния в другое, следующая матрица переходов показывает, сколькими способами можно перейти из каждого начального состояния (левый столбец) в каждое новое состояние. Кстати, на ее правильное построение ушло несколько часов.
Матрица переходов А
| Состояние До | ААААААА | АААААБ | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| АААААБ | 15,626 | 18,780 | 9750 | 2500 | - | - | - | - | - | - | - |
| AAAABB | 4160 | 13,056 | 19 200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1458 | 8748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4098 | 12,348 | 8190 | 2580 | 7920 | 10,080 | 1440 | - | - | - | - |
| AAABBC | 794 | 5172 | 8670 | 5020 | 6480 | 17,280 | 3240 | - | - | - | - |
| AABBCC | 192 | 2304 | 5760 | 3840 | 5760 | 23,040 | 5760 | - | - | - | - |
| AAABCD | 732 | 4464 | 4140 | 1680 | 7920 | 14 400 | 2520 | 4320 | 6480 | - | - |
| AABBCD | 130 | 1,596 | 3150 | 1940 | 5,280 | 16,800 | 3600 | 4800 | 9360 | - | - |
| AABCDE | 68 | 888 | 1380 | 760 | 3960 | 11,520 | 2520 | 7200 | 14,040 | 4320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7200 | 1,800 | 7200 | 16 200 | 10,800 | 720 |
Я не буду вдаваться в долгие рассуждения по матричной алгебре, скажу лишь, что предположим, что матрица B имеет следующий вид:
Матрица B
| Состояние До | АААААБ | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| АААААБ | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| AABBCC | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| AABBCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| AABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
Ответом является отношение определителя матрицы B к определителю матрицы A:
Determ(A) = 1 461 067 501 120 670 000 000 000 000 000 000 000 000 000 000
Determ(B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = приблизительно 9.65599148388557


