WOO logo

Wizard рекомендует

Спросите Волшебника #335

В вашей статье на сайте Wizard of Vegas я прочитал о игре Reversible Royal с доходностью 105,22% . Эта доходность предполагает оптимальную стратегию, включая порядок карт. Какова будет доходность, если предположить средний выигрыш в роял-покере? А если я использую обычную стратегию 6-5 Bonus Poker, которая основана на базовой таблице выплат?

анонимный

При отсутствии отклонений от стратегии, 1 из 60 королевских выпадений будет последовательным. Обратимый джекпот за королевское выпадение составляет 161 556 за 1. Любое другое королевское выпадение приносит 800 за 1. Таким образом, средний выигрыш за королевское выпадение составляет (1/60)*161 556 + (59/60)*800 + 17 396 за 1.

Если предположить, что все игроки, выигравшие королевскую карту, платят 17 396 и используют оптимальную стратегию, основанную на этой победе, то доходность снизится до 103,56%.

Если мы будем играть по стандартной стратегии 6-5 Bonus Poker, которая основана на базовой таблице выплат, то процент возврата снизится еще больше, до 101,97%.

Рассмотрим единичный квадрат с координатами (0,0), (1,0), (1,1), (0,1). Прямая А проходит от (0,0) до (1,1). Прямая В проходит от (1,0) до (0,5,1). Каков радиус окружности, касательной к прямым А, В и основанию окружности?

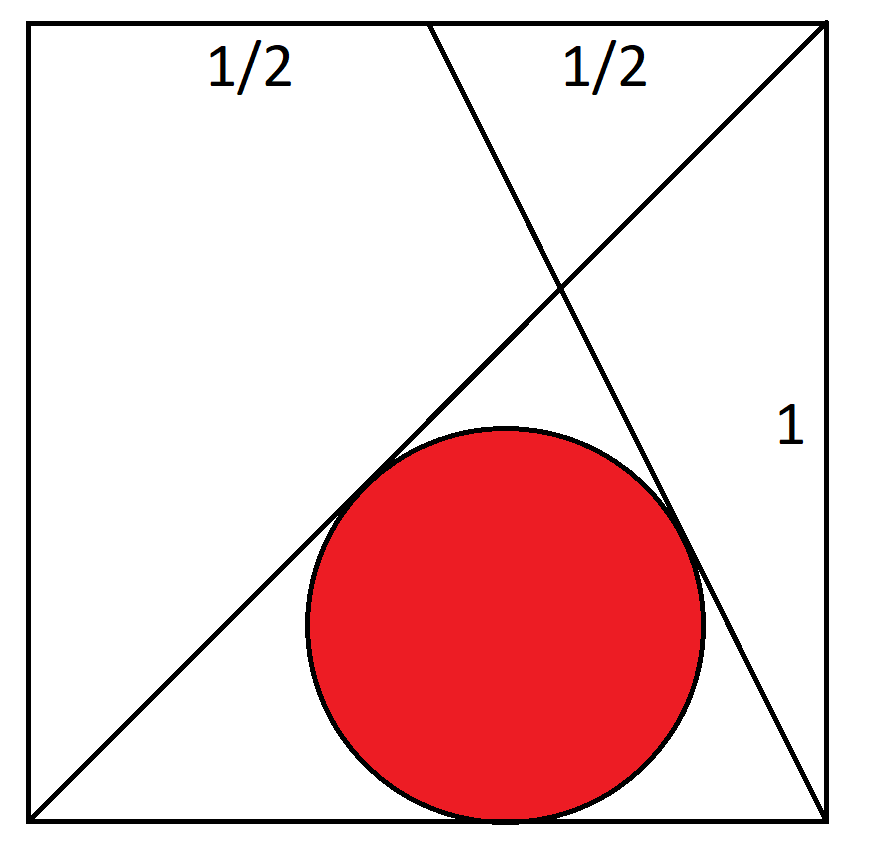
Эта головоломка была опубликована в октябрьском номере журнала Mensa Bulletin за 2020 год.

анонимный

tan(2x)=2tan(x)/(1-tan 2 (x))

Ответ: (1+sqrt(2)+sqrt(5)-sqrt(10))/6 = приблизительно 0,248000646617418.

Вот моё решение (PDF).

Эта проблема задается и обсуждается на моем форуме Wizard of Vegas .

Какова вероятность получить Яхтзи, если это единственная категория, оставшаяся на карточке?

анонимный

Для тех читателей, кто не знаком с игрой в Ятзи, поясним: какова вероятность выпадения пяти одинаковых кубиков при трех бросках пяти кубиков? После каждого броска необходимо выбрать, какие кубики оставить, а какие перебросить.

Ответ: 4,6029%.

[spoiler=Решение]

Вот возможные исходы после первого броска или любого броска, при котором игрок бросает 4 или 5 кубиков.

  • Пять одинаковых карт = 6*(1/6)^5 = 0,000772
  • Четыре одинаковых числа = (1/6)³ * (5/6) * 4 = 0,015432
  • Три одинаковых числа = (1/6)^2*(5/6)^2*COMBIN(4,2) = 0.115741
  • Два одинаковых предмета = 4*(1/6)*(5/6)^3 = 0,385802
  • Единственный в своем роде = 6*5!/6^5 = 0,092593

Вот вероятности после того, как вы скрепили пару.

  • Пять одинаковых карт = (1/6)³ = 0,004630
  • Четыре одинаковых числа = 3*(1/6)^2*(5/6) = 0,069444
  • Три одинаковых числа = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0,370370
  • Два одинаковых = (5/6)³ - 5 * (1/6)³ = 0,555555

Вот вероятности выпадения трёх одинаковых карт:

  • Пять одинаковых карт = (1/6)³ = 0,002778
  • Четыре одинаковых числа = 2*(1/6)*(5/6) = 0,27778
  • Три одинаковых числа = (5/6)² = 0,694444

Вот вероятности выпадения четырех одинаковых карт:

  • Пять одинаковых карт = 1/6 = 0,166667
  • Четыре одинаковых символа = 5/6 = 0,83333

С учетом этих вероятностей перехода, вот вероятности каждого состояния после второго броска кубика:

  • Пять одинаковых карт = 0,000772 + 0,015432*0,166667 + 0,115741*0,002778 + 0,385802*0,004630 + 0,092593*0,000772 = 0,012631
  • Четыре одинаковых числа = 0,015432*0,166667 + 0,115741*0,27778 + 0,115741*0,27778 = 0,116970
  • Три одинаковых числа = 0,115741*0,694444 + 0,385802*0,370370 + 0,092593*0,115741 = 0,409022
  • Два одинаковых символа = 0,385802 * 0,555555 + 0,092593 * 0,385802 = 0,450103
  • Единственный в своем роде = 0,092593 * 0,092593 = 0,008573

Используя те же вероятности продвижения, вот вероятность выигрыша в «Яхтзи» после третьего броска:

Пять одинаковых карт = 0,012631 + 0,116970*(1/6) + 0,409022*(1/6)^2 + 0,450103*(1/6)^3 + 0,008573*(1/6)^4 = 0,046029.

Для тех, кто предпочитает матричную алгебру, существует матрица переходов:

0.092593 0.694444 0.192901 0.019290 0.000772
0.000000 0.555556 0.370370 0.069444 0.004630
0.000000 0.000000 0.694444 0.277778 0.027778
0.000000 0.000000 0.000000 0.833333 0.166667
0.000000 0.000000 0.000000 0.000000 1.000000

Если приведенная выше матрица равна M, то состояние после трех бросков будет M 3 , следующим образом:

0.000794 0.256011 0.452402 0.244765 0.046029
0.000000 0.171468 0.435814 0.316144 0.076575
0.000000 0.000000 0.334898 0.487611 0.177491
0.000000 0.000000 0.000000 0.578704 0.421296
0.000000 0.000000 0.000000 0.000000 1.000000

Вероятность выпадения Ятзи после трех бросков можно найти в ячейке в правом верхнем углу.

[/спойлер]

После просмотра сериала «Ход королевы» я заметил, что ни одна из партий не закончилась ничьей. Мне казалось, что в шахматах высокого уровня часто бывают ничьи. Какой процент партий заканчивается ничьей в шахматах уровня гроссмейстера?

анонимный

Согласно статье «Увеличилось ли количество ничьих в шахматах?» на сайте ChessBase.com, автор Цию Чжоу утверждает, что в 78 468 рейтинговых партиях между игроками с рейтингом 2600 и выше (для получения звания гроссмейстера требуется рейтинг 2500) были получены следующие результаты:

  • Победы чернокожих: 18,0%
  • Победа белых: 28,9%
  • Ничья: 53,1%