WOO logo

Wizard рекомендует

Спросите Волшебника #338

Каково среднее количество бросков двух игральных костей, необходимых для получения всех сумм от 2 до 12?

анонимный

Ответ: 769767316159 / 12574325400 = приблизительно 61,2173847639572.

[spoiler=Решение]

Для ответа на этот вопрос можно использовать цепь Маркова, но я предпочитаю дифференциальное исчисление. Ключевой момент заключается в том, что ответ будет тем же, если время между бросками распределено по экспоненциальному закону со средним значением, равным единице. При этом ответ можно выразить как интеграл от 0 до бесконечности от:

1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))

Вы легко можете решить такие интегралы с помощью калькулятора интегралов .

Вы также можете решить любую подобную задачу с помощью моего калькулятора ожидаемого количества испытаний .

[/спойлер]

В центре квадрата находится муравей. Он расположен на расстоянии 17 дюймов от верхнего левого угла, 20 дюймов от верхнего правого угла и 13 дюймов от нижнего правого угла.

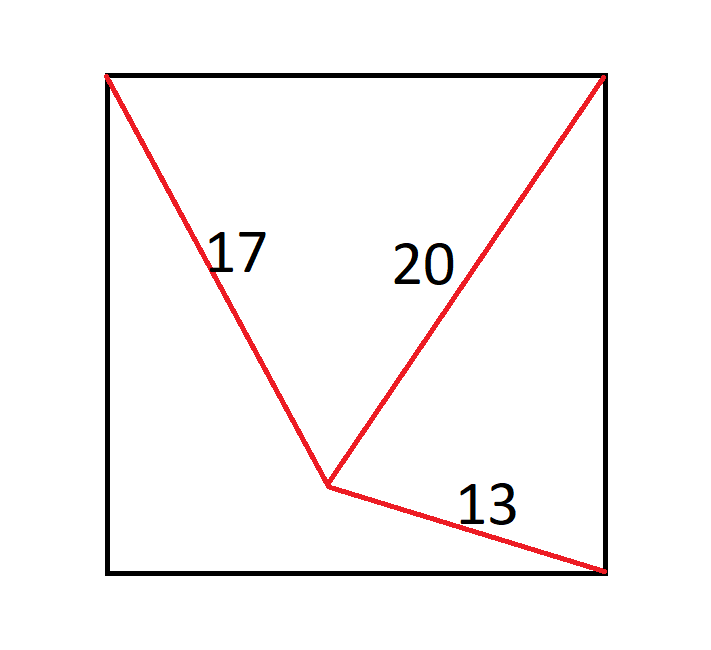
Каков размер квадрата?

анонимный

[спойлер=Полезные формулы] c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b) [/spoiler]

369 квадратных дюймов.

[spoiler=Решение]

Сначала поверните треугольник ABE на 90 градусов, чтобы образовался новый треугольник BDF.

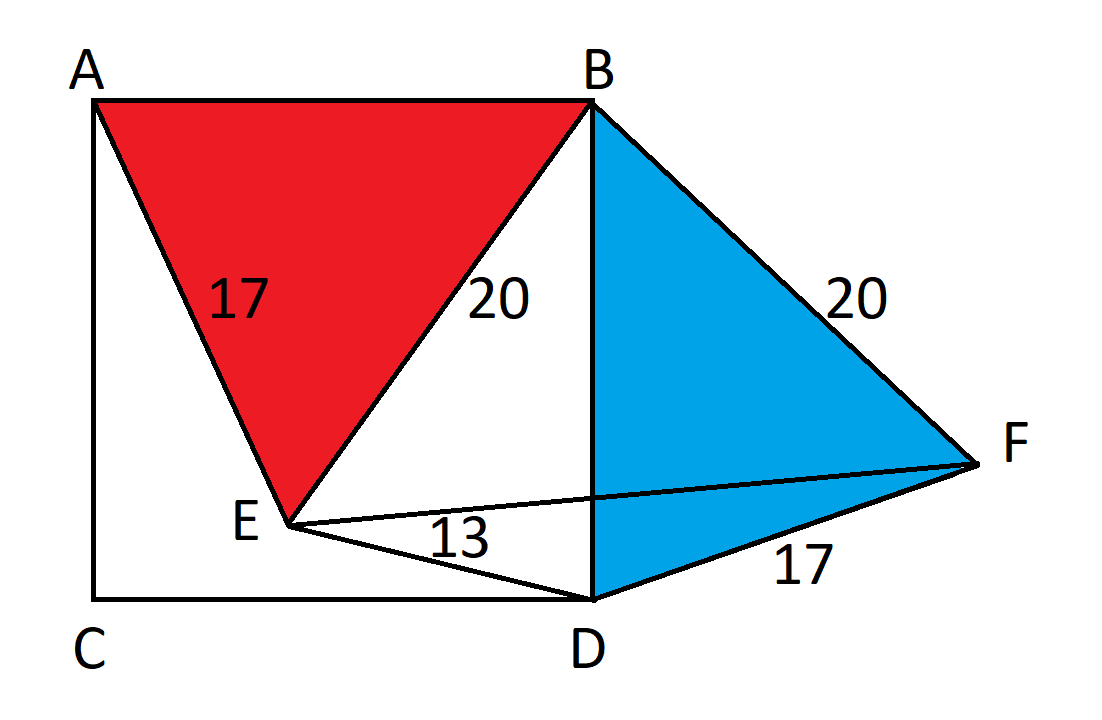
Поскольку треугольник повернут на 90 градусов, угол EBF = 90 градусов по определению. По формуле Пифагора, EF = 20 * √2.

По закону косинусов: 17² = 13² + (20√2)² - 2√13√20√2√cos(DEF).

289 = 169 + 800 - 520*sqrt(2)*cos(DEF)

520*sqrt(2)*cos(DEF) = 680.

cos(DEF) = 17*sqrt(2)/26.

Напомним, что sin²(x) + cos²(x) = 1. Используем это для решения уравнения относительно sin(DEF).

sin²(DEF) + cos²(DEF) = 1

sin²(DEF) + (17*sqrt(2)/26)² = 1

sin²(DEF) + 289/338 = 1

sin²(DEF) = 49/338

sin(DEF) = 7*sqrt(2)/26

Далее рассмотрим угол BED.

Угол BED = Угол BEF + Угол FED.

Мы знаем, что угол EBF равен 90 градусам и является равнобедренным треугольником. Следовательно, угол BEF равен 45 градусам.

Таким образом, угол BED = 45 градусов + угол FED.

Напомним, что cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).

cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - грех(BEF)*sin(FED)

= (1/кв.(2))*17*кв.(2)/26 - (1/кв.(2))*7*кв.(2)/26

= (17/26) - (7/26) = 10/26 = 5/13

Давайте снова применим закон косинусов, на этот раз к треугольнику BED.

BD² = 20² + 13² - 2*20*13*(5/13)

= 400 + 169 - 200 = 369

BD — это сторона рассматриваемого квадрата, поэтому BD² — это площадь этого квадрата, которая, как мы показали, равна 369.

[/спойлер]

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Drop Dead — это игра, в которую играют пятью стандартными кубиками. Вы начинаете свой ход, бросая все пять кубиков. Если ни один из них не выпадает 2 или 5, вы суммируете броски, добавляете сумму к своему счету и бросаете снова. Если выпадают 2 или 5, ваш счет за бросок равен нулю. Все кубики, на которых выпали 2 или 5, объявляются «мертвыми» и откладываются в сторону. Затем вы бросаете снова оставшимися кубиками. Игра продолжается, и вы либо набираете очки, либо убираете кубики. Ваш ход заканчивается, когда все ваши кубики уничтожены, после чего говорят, что вы «умерли». Все ваши броски суммируются для получения вашего окончательного счета. Побеждает тот, у кого больше очков.

Какой результат вы ожидаете увидеть в этой игре?

Gialmere

16.064662

[spoiler=Решение]

Начнём со сценария, когда осталась одна игральная кость, и будем двигаться в обратном направлении.

Пусть переменная a обозначает ожидаемое количество дополнительных очков при наличии одной оставшейся игральной кости.

Среднее значение броска кубика, не равное 2 или 5, составляет (1+3+4+6)/4 = 7/2.

a = (2/3)×(a + 7/2).

а/3 = 7/3.

а = 7.

Далее рассчитаем b, ожидаемое количество очков при наличии двух оставшихся игральных костей.

b = (2/3) 2 ×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.

b = 11,2.

Далее рассчитаем c, ожидаемое количество очков при наличии трех оставшихся кубиков.

c = (2/3) 3 ×(c + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×b + 3×(2/3)×(1/3) 2 ×b.

c = 1302/95 = 13,705263.

Далее рассчитаем d, ожидаемое количество точек при наличии четырех оставшихся игральных костей.

d = (2/3) 4 ×(d + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×c + 6×(2/3) 2 ×(1/3) 2 ×b + 4×(2/3)×(1/3) 3 ×a.

d = 3752/247 = 15,190283.

Наконец, давайте рассчитаем e, ожидаемое количество очков при наличии пяти оставшихся игральных костей.

e = (2/3) 5 ×(e + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×d + 10×(2/3) 3 ×(1/3) 2 ×c + 10×(2/3) 2 ×(1/3) 3 ×b + 5×(2/3)×(1/3) 4 ×a.

e = 16,064662.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

[/спойлер]

Рассмотрим ставку Pairplus в Three Card Poker, которая соответствует таблице выплат 1-4-6-30-40. Однако за мини-роял пик выплачивается джекпот, а за мини-роял в остальных трех мастях — 25% от этого джекпота. Насколько высоким должен быть этот показатель, чтобы ставка считалась честной?

Tolik

Ответ равен 384-кратному размеру ставки.

За каждые дополнительные 100 ставок сверх этого значения доходность увеличивается на 0,79%.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .