WOO logo

Wizard рекомендует

Спросите Волшебника #340

Если казино увеличит выигрыш по ставке на ничью до 9 к 1, по сравнению с обычным коэффициентом 8 к 1, то сколько дополнительных ставок ему потребуется сделать на ничью, чтобы получить тот же ожидаемый выигрыш?

dandolos2000

Вероятность ничьей в баккара составляет 0,095155968.

При обычном выигрыше 8 к 1 ожидаемая прибыль игрока составляет 0,095156 × (8+1) - 1 = -0,143596.

При выигрыше со счетом 9 к 1 ожидаемая прибыль игрока составляет 0,095156 × (9+1) - 1 = -0,048440.

Ожидаемый проигрыш игрока в 0,143596/0,048440 = 2,9643960 раза выше при выигрыше 8 к 1. Таким образом, казино потребуется в 2,9643960 раза больше ставок на ничью, если они увеличат выигрыш до 9 к 1, чтобы ожидаемый выигрыш казино остался тем же.

Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .

Предположим, есть ящик со 100 шарами, пронумерованными от 1 до 100. Десять шаров вынимаются случайным образом без возвращения. Каково среднее число шара с наименьшим номером?

ThatDonGuy

В следующей таблице показано количество комбинаций, вероятность и вклад в наименьшее число (произведение числа и вероятности). В нижней правой ячейке указано, что ожидаемое наименьшее число равно 9,1818182.

Самый низкий мяч

Самый низкий
Мяч		 Комбинации Вероятность Ожидал
Низкий мяч
1 1 731 030 945 644 0.100000 0.100000
2 1 573 664 496 040 0.090909 0.181818
3 1 429 144 287 220 0.082560 0.247681
4 1 296 543 270 880 0.074900 0.299600
5 1 174 992 339 235 0.067878 0.339391
6 1 063 677 275 518 0.061448 0.368686
7 961,835,834,245 0.055564 0.388950
8 868,754,947,060 0.050187 0.401497
9 783,768,050,065 0.045278 0.407498
10 706,252,528,630 0.040800 0.407995
11 635,627,275,767 0.036720 0.403915
12 571,350,360,240 0.033006 0.396076
13 512,916,800,670 0.029631 0.385199
14 459,856,441,980 0.026565 0.371917
15 411,731,930,610 0.023785 0.356780
16 368,136,785,016 0.021267 0.340271
17 328,693,558,050 0.018988 0.322801
18 293,052,087,900 0.016929 0.304728
19 260,887,834,350 0.015071 0.286354
20 231,900,297,200 0.013397 0.267933
21 205,811,513,765 0.011890 0.249680
22 182,364,632,450 0.010535 0.231771
23 161,322,559,475 0.009319 0.214347
24 142,466,675,900 0.008230 0.197524
25 125,595,622,175 0.007256 0.181388
26 110,524,147,514 0.006385 0.166007
27 97,082,021,465 0.005608 0.151425
28 85,113,005,120 0.004917 0.137673
29 74,473,879,480 0.004302 0.124766
30 65,033,528,560 0.003757 0.112708
31 56,672,074,888 0.003274 0.101491
32 49,280,065,120 0.002847 0.091100
33 42,757,703,560 0.002470 0.081512
34 37,014,131,440 0.002138 0.072701
35 31,966,749,880 0.001847 0.064634
36 27,540,584,512 0.001591 0.057276
37 23,667,689,815 0.001367 0.050589
38 20,286,591,270 0.001172 0.044534
39 17,341,763,505 0.001002 0.039071
40 14,783,142,660 0.000854 0.034160
41 12,565,671,261 0.000726 0.029762
42 10 648 873 950 0.000615 0.025837
43 8,996,462,475 0.000520 0.022348
44 7 575 968 400 0.000438 0.019257
45 6 358 402 050 0.000367 0.016529
46 5 317 936 260 0.000307 0.014132
47 4 431 613 550 0,000256 0.012032
48 3 679 075 400 0.000213 0.010202
49 3 042 312 350 0.000176 0.008612
50 2 505 433 700 0.000145 0.007237
51 2 054 455 634 0.000119 0.006053
52 1 677 106 640 0.000097 0.005038
53 1 362 649 145 0.000079 0.004172
54 1 101 716 330 0.000064 0.003437
55 886,163,135 0.000051 0.002816
56 708,930,508 0.000041 0.002293
57 563,921,995 0.000033 0.001857
58 445,891,810 0.000026 0.001494
59 350,343,565 0.000020 0.001194
60 273,438,880 0.000016 0.000948
61 211,915,132 0.000012 0.000747
62 163,011,640 0.000009 0.000584
63 124,403,620 0.000007 0.000453
64 94,143,280 0.000005 0.000348
65 70,607,460 0.000004 0.000265
66 52,451,256 0.000003 0.000200
67 38,567,100 0.000002 0.000149
68 28 048 800 0.000002 0.000110
69 20,160,075 0.000001 0.000080
70 14,307,150 0.000001 0.000058
71 10,015,005 0.000001 0.000041
72 6 906 900 0.000000 0.000029
73 4 686 825 0.000000 0.000020
74 3 124 550 0.000000 0.000013
75 2 042 975 0.000000 0.000009
76 1 307 504 0.000000 0.000006
77 817,190 0.000000 0.000004
78 497,420 0.000000 0.000002
79 293,930 0.000000 0.000001
80 167,960 0.000000 0.000001
81 92,378 0.000000 0.000000
82 48,620 0.000000 0.000000
83 24,310 0.000000 0.000000
84 11,440 0.000000 0.000000
85 5,005 0.000000 0.000000
86 2002 0.000000 0.000000
87 715 0.000000 0.000000
88 220 0.000000 0.000000
89 55 0.000000 0.000000
90 10 0.000000 0.000000
91 1 0.000000 0.000000
Общий 17,310,309,456,440 1.000000 9.181818

Существует более простой способ решения подобных задач, где наименьшее значение шара равно 1. Формула для наименьшего значения шара: (m+1)/(b+1), где m — максимальное значение шара, а b — количество шаров. В данном случае m=100 и n=10, поэтому наименьшее значение шара равно 101/11 = 9,181818.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Следующая головоломка была опубликована в газете New York Times 6 марта 2021 года.

Правила довольно просты:

  1. В каждой строке, столбце и регионе должно быть ровно две звезды.
  2. Две звезды не должны соприкасаться, даже по диагонали.

Можете помочь с решением?

анонимный

Это называется головоломка «Двое не касаются». Кнопка ниже покажет мой ответ и решение.

[спойлер=Ответ]

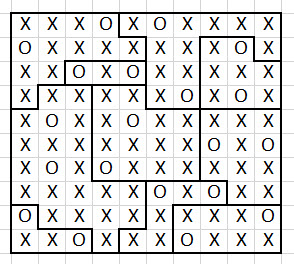
два не прикасаться решено

[/спойлер]

Вот моё решение (PDF).

Каково ожидаемое количество бросков честной шестигранной игральной кости, при котором любая из сторон выпадет шесть раз?

Ace2

Нажмите на кнопку ниже, чтобы увидеть мой ответ.

Ответ: 2597868106693535971 / 131621703842267136 = Приблизительно: 19.73738396371749

Вот моё решение (PDF).