Спросите Волшебника #341
Каково ожидаемое количество бросков двух игральных костей, чтобы получить все суммы от 2 до 12? Пожалуйста, используйте математический анализ для решения.
[spoiler=Решение]
Напомним, что вероятность выпадения суммы 2 равна 1/36. За t бросков ожидаемое количество бросков с суммой 2 составляет t/36. Предположим, что время между бросками распределено экспоненциально со средним значением t/36. Распределение Пуассона показывает, что вероятность выпадения нуля бросков с суммой 2 равна exp(-t/36).
Напомним, что вероятность выпадения суммы 3 равна 2/36 = 1/18. По той же логике, распределение Пуассона говорит нам, что вероятность выпадения нуля с суммой 3 равна exp(-t/18).
Напомним, что вероятность выпадения суммы 4 равна 3/36 = 1/12. По той же логике, распределение Пуассона говорит нам, что вероятность выпадения нуля с суммой 4 равна exp(-t/12).
Напомним, что вероятность выпадения числа 5 равна 4/36 = 1/9. По той же логике, распределение Пуассона показывает, что вероятность выпадения нуля чисел с суммой 5 равна exp(-t/9).
Напомним, что вероятность выпадения суммы 6 равна 5/36. По той же логике, распределение Пуассона говорит нам, что вероятность выпадения нуля с суммой 6 равна exp(-5t/36).
Напомним, что вероятность выпадения суммы 7 равна 6/36 = 1/6. По той же логике, распределение Пуассона говорит нам, что вероятность выпадения нуля с суммой 7 равна exp(-t/6).
Вероятности для чисел от 8 до 12 такие же, как и для чисел от 2 до 6.
Таким образом, вероятность того, что за t единиц каждая сумма выпала хотя бы один раз, составляет:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
Вероятность того, что хотя бы одна сумма НЕ была выброшена за t единиц времени, равна 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
Чтобы получить ожидаемое время без хотя бы одного итогового значения, мы интегрируем приведенную выше функцию от 0 до бесконечности.
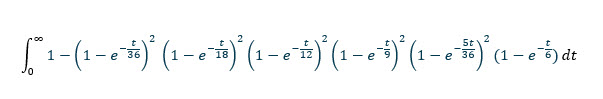
С помощью интегрального калькулятора (я рекомендую этот ) это легко решится: 769767316159/12574325400 = приблизительно 61,2173847639572 рулонов.
[/спойлер]Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Бросайте две игральные кости, красную и синюю, снова и снова. Записывайте сумму бросков каждой кости. Каково ожидаемое количество бросков, прежде чем суммарные значения этих двух костей сравняются?
[spoiler=Больше комментариев]
Трудно объяснить, почему ответ равен бесконечности. Чтобы еще больше запутать и парадоксать ситуацию, вероятность того, что суммы когда-либо сравняются, равна 1.
В следующей таблице показана вероятность того, что итоговые суммы впервые совпадут после 1–16 бросков.
Вероятность равенства сумм впервые
| Роллы | Вероятность |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 13 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
В Excel очень точное соответствие этой кривой определяется формулой y = 0,1784*x-1,011, где x = количество бросков, а y = вероятность.
Сумма этого бесконечного ряда равна бесконечности.
[/спойлер]Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Каков размер джекпота, обеспечивающий безубыточность в игре Pennsylvania Cash 5 ? Налоги и распределение джекпота можно игнорировать.
Для начала давайте рассмотрим правила. Ставка составляет 2 доллара. Игра основана на вытягивании пяти шаров из 43. Вот таблица выплат:
- Совпадение 5 предметов = Джекпот
- Математика 4 = 200 долларов
- Совпадение 3 призов = 10 долларов
- Совпадение 2-х = 2 доллара
Кроме того, игрок получает, как я предполагаю, что-то вроде скретч-карты. Шанс выиграть 6 долларов составляет 1/80, а 2 доллара — 1/5.
В следующей таблице представлен мой анализ базовой игры. Она показывает, что выгода от угадывания от 2 до 4 чисел составляет 0,287784 доллара.
Таблица возврата наличных средств 5
| Ловить | Платит | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|---|
| 5 | джекпот | 1 | 0.000001 | ? |
| 4 | 200 | 190 | 0.000197 | 0.039477 |
| 3 | 10 | 7030 | 0.007303 | 0.073032 |
| 2 | 2 | 84360 | 0.087638 | 0.175276 |
| 1 | 0 | 369075 | 0.383416 | 0.000000 |
| 0 | 0 | 501942 | 0.521445 | 0.000000 |
| Общий | 0 | 962598 | 1.000000 | 0.287784 |
В следующей таблице представлен мой анализ функции мгновенного выигрыша Quick Cash. В нижней правой ячейке указано значение 0,475 доллара.
Таблица мгновенного возврата наличных средств
| Ловить | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| 6 | 1 | 0.012500 | 0.075000 |
| 2 | 16 | 0.200000 | 0.400000 |
| 0 | 63 | 0.787500 | 0.000000 |
| Общий | 80 | 1.000000 | 0.475000 |
Таким образом, стоимость непрогрессивных призов составляет 0,287784 долл. США + 0,475000 долл. США = 0,762784 долл. США.
Пусть j равно значению джекпота, при котором достигается точка безубыточности. Тогда:
2 = 0,762784 + j × (1/962598)
1,237216 = j × (1/962598)
j = 1,237216 × 962598
j = 1 190 941,95 долл. США.
Общая норма доходности составляет 0,381392 плюс 0,051943 на каждые 100 000 долларов джекпота.
Как указано в вопросе, все это не включает налоги и распределение джекпота.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .


