Спросите Волшебника #352
Насколько максимальные выплаты увеличивают преимущество казино в конном заводе Mississippi Stud?
Хороший вопрос. Игрокам в Mississippi Stud определенно следует знать, что максимальные выплаты могут уменьшить их выигрыш при роял-флеше, что увеличивает преимущество казино.
В Mississippi Stud максимальный выигрыш за роял-флеш составляет 500 к 1, и он применяется ко всем ставкам. У игрока есть две попытки повысить ставку до 3-кратного размера анте, поэтому его финальная ставка может достигать 7-кратного размера анте. Если игрок надеется на роял-флеш, он должен максимально повышать ставки.
Максимальная ставка, которую игрок может сделать на «Анте» в Mississippi Stud, без ограничения выплат, составляет максимальную выплату/3500. Например, если максимальная выплата составляет 80 000 долларов, то я рекомендую сделать максимальную ставку на «Анте» в размере 22,86 доллара. Я бы округлил это значение до 20 долларов.
В следующей таблице показано преимущество казино при различных размерах ставок и типичных максимальных выигрышах. Таблица предполагает оптимальную стратегию игрока без ограничения выигрышей. Обратите внимание, как преимущество казино увеличивается с увеличением размера ставки и уменьшением максимального выигрыша.
Преимущество казино с ограничением выплат
| Ставка | Ограничение в 50 000 долларов | Ограничение в 80 000 долларов | Ограничение в 100 000 долларов |
|---|---|---|---|
| 15 долларов | 5,02% | 4,91% | 4,91% |
| 20 долларов | 5,15% | 4,91% | 4,91% |
| 25 долларов | 5,22% | 5,04% | 4,91% |
| 50 долларов | 5,38% | 5,28% | 5,22% |
| 75 долларов | 5,49% | 5,37% | 5,33% |
| 100 долларов | 5,64% | 5,41% | 5,38% |
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
В казино Vital Vegas игрока отчитали за то, что он оставил чаевые всего в 200 долларов при джекпоте в 1,1 миллиона долларов. Каков правильный этикет при оставлении чаевых в такой ситуации?
Да, хотя они и ругают игрока за небольшие чаевые, они предусмотрительно уклоняются от вопроса о том, какими должны быть уместные чаевые.
Правила чаевых четко определены не только для крупных джекпотов, но и для небольших. Мнения на этот счет очень разнятся, и многие из них принадлежат людям, которые никогда не выигрывали джекпот.
Во-первых, позвольте мне подчеркнуть, что чаевые не являются необязательными. В казино принято оставлять чаевые за полученное обслуживание, в зависимости от суммы выигрыша и уровня обслуживания. Легко впасть в ярость и начать оправдывать, почему вообще не следует оставлять чаевые. Система чаевых, безусловно, несовершенна, но это та система, которая у нас есть. Если вы не согласны и отказываетесь оставлять чаевые, то не просите о той услуге, за которую принято оставлять чаевые.
Во-вторых, после того, как установлено, игрок должен оставить чаевые за джекпот, сколько? Я ограничиваю это обсуждение ситуацией, когда игрок выигрывает только один джекпот. Правила меняются, если игрок выигрывает много джекпотов, что обычно происходит при очень высоких ставках. Напомню, правила оформления документов на джекпот следующие:
- Выигрыш в размере 1200 долларов или более на игровых автоматах.
- Выигрыш в кено в размере 1500 долларов или более.
- Выигрыш в размере 5000 долларов или более в покерном турнире.
- Выигрыш в размере 600 долларов или более И как минимум в 300 раз превышающий сумму ставки в настольных играх.
Какую сумму я рекомендую оставить чаевые? Раньше я говорил от 0,5% до 2% от джекпота, чем больше джекпот, тем ниже процент. Однако тогда я не думал о таких крупных джекпотах. Думаю, этот диапазон уместен до суммы примерно в 100 000 долларов.
Этот вопрос побудил меня создать особую формулу, которая, как мне кажется, подходит для любого джекпота от 1200 долларов до миллионов. Вот она:
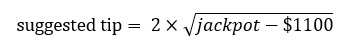
Если вы не видите изображение, то это 2×sqrt(джекпот - 1100 долларов).
Вот что показывает формула для некоторых распространенных сумм джекпота.
Рекомендуемая таблица советов
| Джекпот | Кончик |
|---|---|
| 1200 долларов | 20 долларов |
| 2000 долларов | 60 долларов |
| 5000 долларов | 125 долларов |
| 10 000 долларов | 189 долларов |
| 20 000 долларов | 275 долларов |
| 50 000 долларов | 442 доллара |
| 100 000 долларов США | 629 долларов |
| 1 000 000 долларов США | 1999 долларов США |
В случае с суммой в 1,1 миллиона долларов моя формула предполагает 2096,57 долларов. Думаю, можно округлить до 2000 долларов в меньшую сторону. Конечно, следует также учитывать другие факторы, такие как качество обслуживания.
Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
Для любого большого числа, каково среднее расстояние между простыми числами, близкими к этому числу? Также, сколько простых чисел меньше этого числа?
Очень хорошей оценкой среднего расстояния между простыми числами вблизи любого большого числа n является ln(n). Удивительно, насколько хороша эта оценка.
В качестве доказательства в следующей таблице показан диапазон первых 15 миллионов простых чисел, сгруппированных по одному миллиону. В таблице показано среднее расстояние между простыми числами в этом диапазоне и оценка среднего расстояния. Оценка представляет собой натуральный логарифм среднего значения наибольшего и наименьшего простого числа в диапазоне. Например, для 15-й группы из миллиона простых чисел это ln((256 203 221 + 275 604 541)/2).
Среднее расстояние между простыми числами
| Первый прайм в диапазоне | Последний прайм в диапазоне | Простые числа в диапазоне | Среднее расстояние | Оценивать | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1 000 000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1 000 000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1 000 000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1 000 000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1 000 000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1 000 000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | 1 000 000 | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | 1 000 000 | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | 1 000 000 | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | 1 000 000 | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | 1 000 000 | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | 1 000 000 | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | 1 000 000 | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | 1 000 000 | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | 1 000 000 | 19.40132 | 19.39864545 |
Источник: Раздел «Промежутки между праймами» на Prime Pages.
Чтобы вычислить количество простых чисел, меньших любого заданного числа, мы можем начать с интегрирования оценки среднего расстояния ln(n). Это даст нам сумму средних расстояний между простыми числами до любого числа n.
Чему равен интеграл от f(n)=ln(n)? Напомним, что интегрирование по частям дает нам:
Интеграл f(n)*g'(n) dn = f(n)*g(n) - интеграл (f'(n)*g(n)) dn
Пусть f(n) = ln(n) и g'(n) = 1. Тогда f'(n) = 1/n и g(n) = n. Таким образом, интеграл от ln(n) будет равен ln(n)*n - интеграл от ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
Если разделить n*(ln(n)-1) на n, мы получим среднее расстояние между простыми числами в диапазоне от 2 до n. Это ln(n)-1.
Если разделить n на это среднее расстояние между простыми числами, мы получим среднее число простых чисел меньше n, равное n/(ln(n)-1).
В качестве доказательства в следующей таблице показано количество простых чисел при различных больших числах и их приблизительное значение. Прошу прощения за точность до 15 значащих цифр, это всё, что позволяет Excel. Кто-нибудь, пожалуйста, создайте электронную таблицу, которая сможет обрабатывать большее количество знаков после запятой.
Среднее расстояние между простыми числами
| н | Простые числа при n | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1000 | 168 | 169 |
| 10 000 | 1,229 | 1,218 |
| 100,000 | 9,592 | 9,512 |
| 1 000 000 | 78,498 | 78,030 |
| 10 000 000 | 664,579 | 661,459 |
| 100 000 000 | 5 761 455 | 5 740 304 |
| 1 000 000 000 | 50,847,534 | 50,701,542 |
| 10 000 000 000 | 455,052,511 | 454,011,971 |
| 100 000 000 000 | 4 118 054 813 | 4,110,416,301 |
| 1 000 000 000 000 | 37,607,912,018 | 37,550,193,650 |
| 10 000 000 000 000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3 204 941 750 802 | 3,201,414,635,781 |
| 1 000 000 000 000 000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10 000 000 000 000 000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2 623 557 157 654 230 | 2 621 647 966 812 030 |
| 1 000 000 000 000 000 000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10 000 000 000 000 000 000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2 220 819 602 560 910 000 | 2 219 671 974 013 730 000 |
| 1 000 000 000 000 000 000 000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10 000 000 000 000 000 000 000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1 925 320 391 606 800 000 000 | 1 924 577 459 166 810 000 000 |
| 1 000 000 000 000 000 000 000 000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10 000 000 000 000 000 000 000 000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
Источник: Сколько простых чисел существует? на Prime Pages.


