Спросите Волшебника #353
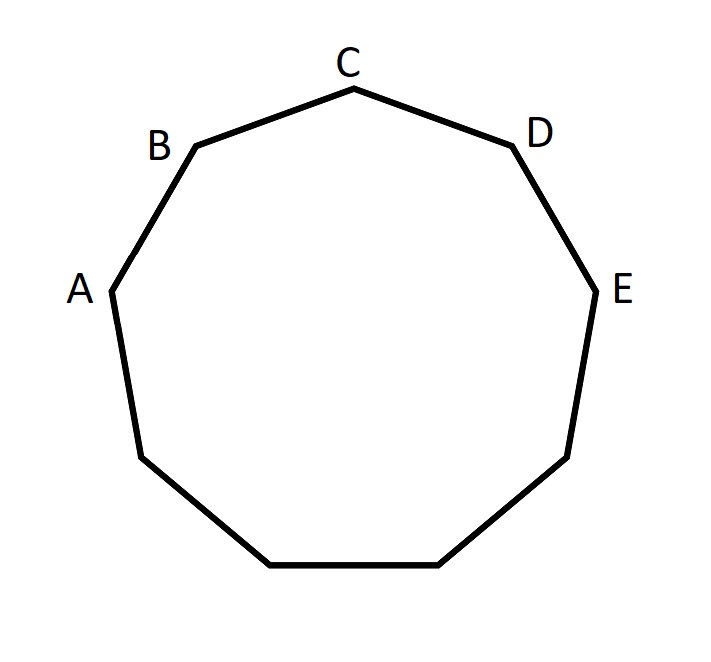
На рисунке выше изображен девятиугольник со стороной длиной один.
Что больше, AB+AC или AE?
Данная задача взята из номера журнала Mensa Bulletin за март 2021 года.
Вот моё решение этой проблемы. (PDF)
Как легко найти квадратный корень любого трех- или четырехзначного числа, если ответ является целым числом?
В следующей таблице показаны числа от 0 до 9, квадрат каждого из них и последняя цифра этого квадрата.
Последняя цифра квадратных чисел
| Оригинал Число | Квадрат | Последняя цифра квадрата |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
Обратите внимание, что четные квадраты чисел всегда оканчиваются на 0, 1, 4, 5, 6 или 9. Это верно для всех квадратов. Это происходит потому, что последняя цифра исходного числа определяет последнюю цифру квадрата.
Шаг 1: Исходя из последней цифры квадрата, мы можем использовать следующую таблицу, чтобы определить последнюю цифру квадратного корня. Например, если квадратом является число 2809, то последняя цифра квадратного корня — 3 или 7.
Последняя цифра исходного числа
| Последняя цифра квадратного корня | Последняя цифра квадрата |
|---|---|
| 0 | 0 |
| 1 | 1 или 9 |
| 4 | 2 или 8 |
| 5 | 5 |
| 6 | 4 или 6 |
| 9 | 3 или 7 |
Шаг 2: Далее возьмите исходное число и отбросьте две правые цифры. Например, если исходное число было 2809, то используйте 28.
Шаг 3: Найдите наименьшее квадратное число, меньшее или равное результату шага 2. Затем извлеките квадратный корень из этого квадратного числа. Например, наименьшее квадратное число, меньшее 28, равно 25. Извлечем квадратный корень из 25, получим 5.
Если вы не запомнили все квадраты до 100, то можете воспользоваться следующей таблицей.
Первая часть квадратного корня
| Шаг 2 | Шаг 3 |
|---|---|
| от 1 до 3 | 1 |
| от 4 до 8 | 2 |
| от 9 до 15 | 3 |
| от 16 до 24 | 4 |
| от 25 до 35 | 5 |
| 36–48 | 6 |
| 49–63 | 7 |
| от 64 до 80 | 8 |
| 81–99 | 9 |
Шаг 4: Если результат шага 1 равен 0 или 5, то укажите это значение после результата шага 3, и на этом всё.
В противном случае, пусть a = результат шага 3. Пусть b = a × (a + 1). Например, если результат шага 3 равен 5, то b = 5 × 6 = 30.
Шаг 5: Если b < a, то последняя цифра квадратного корня — это наименьшее из возможных значений из шага 1. В противном случае, если b >= a, то это большее из двух возможных значений.
Шаг 6: Чтобы извлечь квадратный корень, возьмите результат из шага 3, а затем результат из шага 5. Другими словами, 10 × (шаг 3) + шаг 5.
Рассмотрим несколько примеров:
Найдите квадратный корень из 256.
- Шаг 1: Последняя цифра квадратного корня равна 4 или 6.
- Шаг 2: Отбросив последние две цифры, получаем 2.
- Шаг 3: Наименьший квадрат, меньший или равный 2, равен 1. Квадратный корень из 1 равен 1.
- Шаг 4: 1*(1+1) = 2.
- Шаг 5: Результат шага 4 равен результату шага 2, поэтому в качестве последней цифры мы используем большее из значений шага 1, то есть 6.
- Шаг 6: Квадратный корень — это результат из шага 5, к которому добавляется результат из шага 3, в результате получаем 1 и 6 = 16.
Найдите квадратный корень из 1369.
- Шаг 1: Последняя цифра квадратного корня равна 3 или 7.
- Шаг 2: Отбросив последние две цифры, получаем 13.
- Шаг 3: Наименьший квадрат, меньший или равный 13, равен 9. Квадратный корень из 9 равен 3.
- Шаг 4: 3*(1+3) = 12.
- Шаг 5: Результат шага 2 больше результата шага 4, поэтому в качестве последней цифры мы используем большее из значений шага 1, то есть 7.
- Шаг 6: Квадратный корень — это результат сложения 3 и результата шага 5, в результате получаем 3 и 7 = 37.
Найдите квадратный корень из 2704.
- Шаг 1: Последняя цифра квадратного корня равна 2 или 8.
- Шаг 2: Отбросив две последние цифры, получаем 27.
- Шаг 3: Наименьший квадрат, меньший или равный 27, равен 25. Квадратный корень из 25 равен 5.
- Шаг 4: 5*(1+5) = 60.
- Шаг 5: Результат шага 2 меньше результата шага 4, поэтому в качестве последней цифры мы используем меньший из вариантов шага 1, то есть 2.
- Шаг 6: Квадратный корень — это результат из шага 5, к которому добавляется результат из шага 3, в результате получаем 5 и 2 = 52.
Найдите квадратный корень из 5625.
- Шаг 1: Последняя цифра квадратного корня — 5.
- Шаг 2: Отбросив две последние цифры, получаем 56.
- Шаг 3: Наименьший квадрат, меньший или равный 56, равен 49. Квадратный корень из 49 равен 7.
- Шаг 4: Результат шага 1 равен 0 или 5, поэтому ответ — это результат шага 3, к которому добавлен результат шага 1: 7 и 5 = 75
Найдите квадратный корень из 6561.
- Шаг 1: Последняя цифра — 1 или 9.
- Шаг 2: Отбросив две последние цифры, получаем 65.
- Шаг 3: Наименьший квадрат, меньший или равный 65, равен 64. Квадратный корень из 64 равен 8.
- Шаг 4: 8*(1+8) = 72.
- Шаг 5: Результат шага 2 меньше результата шага 4, поэтому в качестве последней цифры мы используем меньшее из значений шага 1, то есть 1.
- Шаг 6: Квадратный корень — это результат из шага 5, к которому добавляется результат из шага 3, в результате получаем 8 и 1 = 81.
Демонстрацию этого метода можно посмотреть на YouTube .
Какова вероятность получить 60 или более выигрышей подряд за 12 часов игры в блэкджек?
Согласно моим наблюдениям на странице, посвященной вариативности блэкджека и основанной на либеральных правилах Стрипа, вероятности выигрыша, ничьей или проигрыша следующие:
- Победа — 42,43%
- Push — 8,48%
- Убыток — 49,09%
Давайте не будем учитывать ничьи, и тогда вероятность выигрыша, при условии, что раздача закончится победой или поражением, составит 46,36%.
Давайте примем скорость игры за 100 раздач в час.
Вероятность увидеть хотя бы одну серию из не менее 60 раздач подряд можно приблизительно оценить следующим образом:
100×12×0,4636 60 = 1 из 89 412 355 233 588 500.Для сравнения, если вы купили один билет Powerball и один билет Megamillions, вероятность выигрыша в обоих составит 1 к 88 412 922 115 818 300.
Таким образом, вероятность выиграть в обеих лотереях немного выше, чем вероятность одержать 60 побед подряд за 12 часов игры.


