Спросите Волшебника #355
В фильме «Лицензия на убийство» Джеймс Бонд играет в блэкджек три раунда, разыгрывая по пять карт за раз. Я заметил, что он ни разу не взял дополнительную карту ни в одном из раундов. Какова вероятность такого совпадения?
Видеозапись этой сцены можно найти на YouTube .
В игре действительно встречается подозрительно большое количество крупных карт, не так ли? Вот карты, которые мне удалось различить. Обратите внимание, что в некоторых случаях карты были видны нечётко.
Лицензия на убийство — Наблюдаемые ряды
| Классифицировать | Наблюдалось |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| Дж. | 3 |
| В | 6 |
| К | 4 |
| А | 1 |
| Общий | 35 |
Вы совершенно правы, Бонд не берет ни одной карты ни в одной из своих 15 начальных раздач. Он один раз разделяет восьмерки, но после разделения тоже не берет ни одной карты. Вот подсчет его начальных действий во всех 15 раздачах:
- Двойной — 1
- Разделение — 1
- Стойка — 13
Вот основные вероятности стратегий для каждого начального действия, предполагающие шесть колод, удвоение ставки после разделения, подглядывание дилером в закрытую карту и остановку дилера при мягкой 17.
Блэкджек — Вероятности первого действия
| Действие | Вероятность |
|---|---|
| Стоять | 43,46% |
| Ударять | 39,78% |
| Двойной | 9,53% |
| Расколоть | 2,48% |
| Блэкджек | 4,75% |
| Общий | 100.00% |
Если бы сдача была разрешена, эта вероятность составила бы 4,14%, исходя из вероятности остаться в игре.
Следует отметить, что однажды у Бонда было 16 очков против 10. Основная стратегия заключается в том, чтобы взять эту карту, но это очень рискованно. Учитывая обилие десяток в той раздаче, Бонд, возможно, знал, что счет высокий, что привело бы к исключению из основной стратегии — взятию карты в такой ситуации.
Вероятность не получить выигрыш ни в одной раздаче составляет 60,22%. Вероятность не получить выигрыш в 15 из 15 раздач, при условии независимости каждой раздачи, составляет 0,602162 15 = 0,000496253 = приблизительно 1 раз в 2015 году.
В игре «Игра в кальмара» 16 игроков соревнуются на стеклянном мосту. Мост разделён на 18 пар стеклянных секций. В каждой паре одна секция закалённая и может выдержать вес игрока. Другая секция — обычное стекло, которое разобьётся под весом игрока. Если игрок наступит на обычную секции, он разобьёт её и упадёт насмерть.
Игроки должны продвигаться вперед по одному в заранее определенном порядке.
Предположим, что при выборе каждой пары стеклянных ступенек игроки выбираются случайным образом. Каково ожидаемое количество игроков, которые смогут безопасно перейти ступеньку?
Я помещу ответ и решение в спойлер, чтобы все желающие могли сами найти ответ.
Вероятность того, что игрок 1 безопасно пересечет границу, составляет (1/2)^18 = 1/262144 = приблизительно 0,000004.
Игрок 2 может безопасно пересечь границу двумя способами:
- Игрок 1 благополучно переходит дорогу. В этом случае игрок 2 может просто повторить его действия.
- Между игроком 1 и игроком 2 может быть только один неудачный шаг. Это может произойти при 18 из 18 возможных пар стаканов. Вероятность 17 удачных шагов и одного неудачного шага составляет 18*(1/2)^2 = 18/262144 = 0,000069.
Таким образом, вероятность того, что игрок 2 безопасно пересечет границу, составляет 0,000004 + 0,000069 = 0,000072.
Игрок 3 может безопасно пересечь границу двумя способами:
- Игрок 2 благополучно переходит дорогу. В этом случае игрок 3 может просто повторить его действия.
- Между игроками 1, 2 и 3 всего два неудачных шага. Существует 153 способа выбрать 2 из 18 пар стеклянных фигур для двух фигур, которые убивают игроков 1 и 2. Вероятность 16 удачных шагов и двух неудачных шагов составляет 153*(1/2)^2 = 153/262144 = 0,000584.
Таким образом, вероятность того, что игрок 3 безопасно пересечет линию, составляет 0,000072 + 0,000584 = 0,000656.
Игрок 4 может безопасно пересечь границу двумя способами:
- Игрок 3 благополучно переходит дорогу. В этом случае игрок 4 может просто повторить его действия.
- Между игроками с 1 по 4 всего три неудачных шага. Существует комбин (18,3) = 816 способов выбрать 3 из 18 пар стеклянных фигур для двух фигур, которые убивают игроков с 1 по 3. Вероятность 15 удачных шагов и 3 неудачных шагов составляет 816*(1/2)^2 = 816/262144 = 0,003113.
Следуя этой логике, мы получаем следующую таблицу вероятностей для каждого игрока.
Бридж
| Игрок | Вероятность Выживание |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 13 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| Общий | 7.000076 |
Чтобы выразить ответ в замкнутой форме, это:
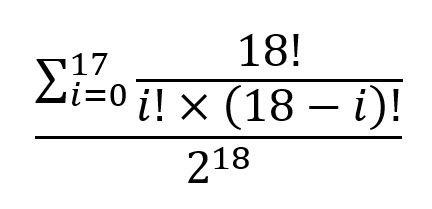
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
В вашей игре Ultimate X Gold , на отметке 3:10 вам выпал фулл-хаус, тройки поверх четверок. Ваш множитель для любой четверки от двойки до четверки был 9x. Множитель для фулл-хауса был 1x. Почему вы сохранили фулл-хаус, а не просто три тройки и не попытались собрать четверку с большим множителем?
Ты прав, я совершенно всё испортил этой рукой.
Напомним, я играл в 10 партий. Таким образом, мой выигрыш с фулл-хаусом составил 10×35 = 350.
Имея в руках только тройки, каждая рука имела следующие вероятности:
- Четыре одинаковых символа — 4,26%
- Полный зал — 6,11%
- Три одинаковых предмета — 89,64%
Вот выигрыши по каждой раздаче после применения множителей:
- Четыре одинаковых — 1800
- Полный зал — 35
- Три одинаковых — 15
Моя ожидаемая прибыль, если бы у меня была только тройка, составила бы (4,26% * 1800) + (6,11% * 35) + (89,64% * 15) = 92,17854. Это значительно больше, чем 35, которые дает фулл-хаус. Так что да, я допустил досадную ошибку с этой раздачей.
Кто-то предложил мне пари. Я должен выбрать любые три ранга из стандартной покерной колоды, записать свой прогноз, но держать его в секрете до конца. Например, 7-туз-2. Затем он предложил мне пари, что сможет назвать хотя бы один из моих рангов, если угадает три раза. Каковы были мои шансы на победу?
Чтобы выиграть, ваш противник должен ошибиться во всех трех прогнозах. Вероятность неверного первого прогноза составляет 10/13. Вероятность неверного второго прогноза — 9/12, поскольку мы можем исключить первый угаданный ранг из числа возможных вариантов. Вероятность неверного третьего прогноза — 8/11, поскольку мы можем исключить первые два угаданных ранга из числа возможных вариантов.
Для вашей победы должны произойти все три этих события. Таким образом, ваши шансы на победу составляют (10/13) * (9/12) * (8/11) = 720/1716 = 41,96%.
При равных шансах преимущество казино на этой ставке с вашей стороны составляет 16,08% (ой!).
Этот вопрос взят из книги Оуэна Э'Ши «Книга о пари на предложения» (номер 7).


