Спросите Волшебника #367
Мне нравится ставить все числа в крэпсе. Сколько уникальных чисел я могу ожидать, прежде чем выпадет 7?
Для удобства других читателей поясним: вопрос сводится к тому, сколько из следующих сумм выпадут на двух игральных костях, прежде чем сумма достигнет семи: 4, 5, 6, 8, 9 и 10.
Ответ — 2,375758. В следующей таблице показана вероятность выпадения от нуля до шести уникальных сумм в указанном диапазоне для каждой отдельной возможности. В нижней правой ячейке показано среднее количество уникальных сумм, выпавших до семерки.
Выпали уникальные числа
| Общий | Вероятность | Ожидал |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| Общий | 1.000000 | 2.375758 |
Правда ли, что при подбрасывании честной монеты вероятность выпадения лицевой стороной вверх той же монеты, которая изначально лежала лицевой стороной вверх?
Имеющиеся данные свидетельствуют об обратном!
Перси Диаконис и Сьюзан Холмс из Стэнфордского университета провели 10 000 подбрасываний монеты. Монета выпадала той же стороной вверх, что и в начале, в 50,8% случаев (источник: «Решение на 51 процент» из информационного бюллетеня «Что происходит в математических науках» Американского математического общества). Вероятность получения такого высокого или более высокого соотношения составляет 5,48%.
Чтобы доказать это математически, я предположил, что фактическое число оборотов монеты подчиняется распределению Пуассона. Точнее, если среднее число оборотов равно m, то вероятность ровно n оборотов равна exp(-m)*m^n/n!. Для иллюстрации распределения Пуассона на следующем графике показана вероятность от 0 до 25 оборотов при среднем значении 10.
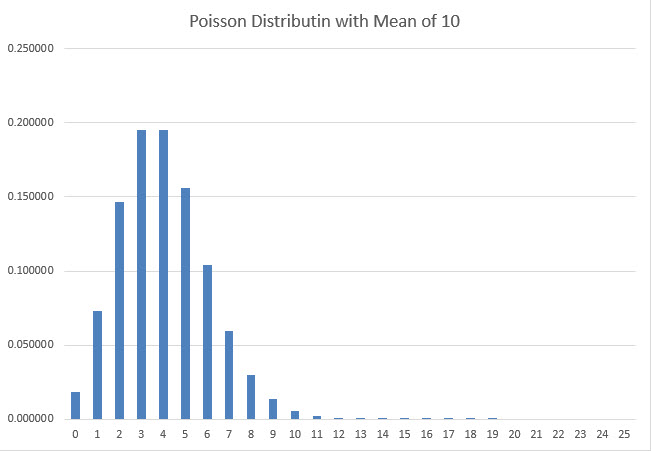
Причина, по которой я выбрал предположение о распределении Пуассона, заключается в том, что при достаточно больших средних значениях оно имеет форму, близкую к колоколообразной, а фактический результат никогда не может быть ниже нуля.
Затем я рассчитал вероятность четного числа полуоборотов (в результате которых та же сторона окажется вверху, что и в исходном положении) для различных средних значений полуоборотов. В следующей таблице показаны результаты для средних значений от 0,5 до 5,0.
Вероятность четного и нечетного числа оборотов
| Средние революции | Ровный итог | Нечетное общее количество |
|---|---|---|
| 0,5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
Затем меня заинтересовало, почему вероятность четного числа всегда больше 50%. Оказалось, что вероятность четного числа при среднем значении m может быть выражена как 0,5 + e^(-2m)/2. e в любой степени должно быть положительным, следовательно, вероятность четного числа оборотов также положительна.
Доказательство этой формулы вы можете увидеть здесь .
Каков ваш анализ игры Spelling Bee в программе Price is Right?
Для удобства других читателей позвольте мне сначала кратко изложить правила.
- На игровом поле находятся 30 карт, пронумерованных от 1 до 30.
- На оборотной стороне каждой карточки находится буква или слово «car». Распределение каждой карточки следующее:
- C: 11
- А: 11
- Р: 6
- Автомобиль: 2
- Ведущий позволяет игроку выбрать две карты.
- После игры на определение цены, в которую я не буду вдаваться, у игрока появляется возможность заработать до трех дополнительных карт.
- Карты будут перевернуты.
- Игрок может выиграть автомобиль двумя способами:
- Игрок получает как минимум одну карту каждой буквы (таким образом, получается слово CAR).
- Игрок получает как минимум одну из карт "CAR".
- В любой момент игры игрок может сдаться и получить 1000 долларов за каждую неперевернутую карту.
Вот видеоролик с игрой.
В следующей таблице показана вероятность выигрыша в зависимости от количества карт у игрока, при условии, что ни одна из них еще не была перевернута.
Конкурс правописания — Вероятность выигрыша
| Карты | Вероятность Победа |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
Прежде чем перевернуть карты, игрок не должен сдаваться, предполагая, что автомобиль имеет разумную стоимость. Например, даже имея всего две карты, у игрока есть 13,1% шанс получить хотя бы одну карту АВТОМОБИЛЬ. Игроку должно быть все равно, если стоимость автомобиля составляет 15 263,16 долларов, а стоимость нового автомобиля — 2000 долларов.
Ниже приведены точки безразличия к стоимости автомобиля в зависимости от количества неперевернутых карт у игрока.
Конкурс правописания — Вероятность выигрыша
| Карты | Безразличие Точка |
|---|---|
| 2 | 15 263,16 долларов США |
| 3 | 8 066,23 долл. США |
| 4 | 6 849,11 долларов США |
| 5 | 6 803,75 долларов США |


