Спросите Волшебника #373
Уверена, вы поклонница «Теории большого взрыва». Одна из моих любимых сцен — это игра «Камень, ножницы, бумага» с Ящером Споком. Это как игра в «Камень, ножницы, бумага» с пятью символами, правила которой следующие:
- Бумага покрывает камень
- Камень давит ящерицу
- Яды ящериц Спок
- Спок разбивает ножницы
- Ножницы режут бумагу
- Ящерица ест бумагу Спок испаряет камень
- Ножницы обезглавливают ящерицу
- Бумага опровергает слова Спока
- Раздавливание камней ножницами
Мой вопрос: можно ли добавить больше символов, чтобы у каждой стороны были одинаковые шансы против случайного игрока?
Да, мне тоже очень нравится эта сцена! Вот видео с ней на YouTube .
Вам нужно нечётное количество символов. Теоретически, можно использовать чётное количество, но тогда придётся устанавливать правила, при которых определённые пары разных символов приведут к ничьей. Нет, нам нужна решающая игра, где ничья возможна только в том случае, если оба игрока выберут один и тот же символ.
Одно из решений особенно элегантно и легко объясняется с помощью простого числа символов. Позвольте мне объяснить на примере семи символов. Обозначим символы от A до G и изобразим их на круге на следующей диаграмме.
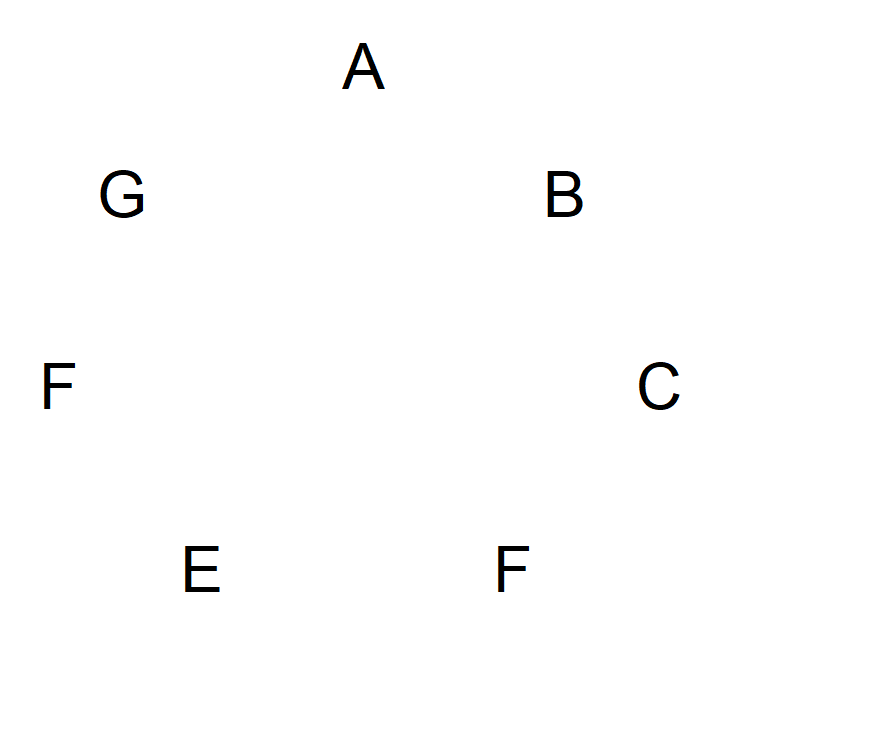
Далее, начните с символа А и нарисуйте стрелку по часовой стрелке к следующему символу. Стрелка должна указывать на то место, которое находится между этими двумя. Представьте, что этот символ поражен стрелой. Продолжайте двигаться по часовой стрелке, пока не вернетесь к символу А. Диаграмма не будет выглядеть так:
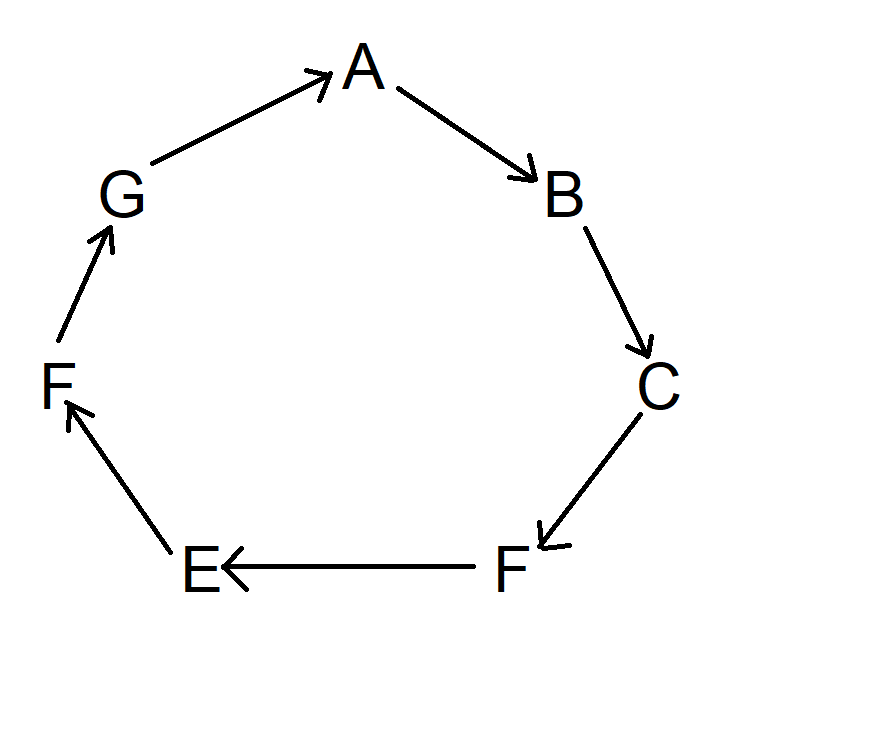
Далее проделайте то же самое, но переместитесь на два символа по часовой стрелке, начиная с точки А. На самом деле, вы можете начать с любого места. Теперь диаграмма выглядит так:
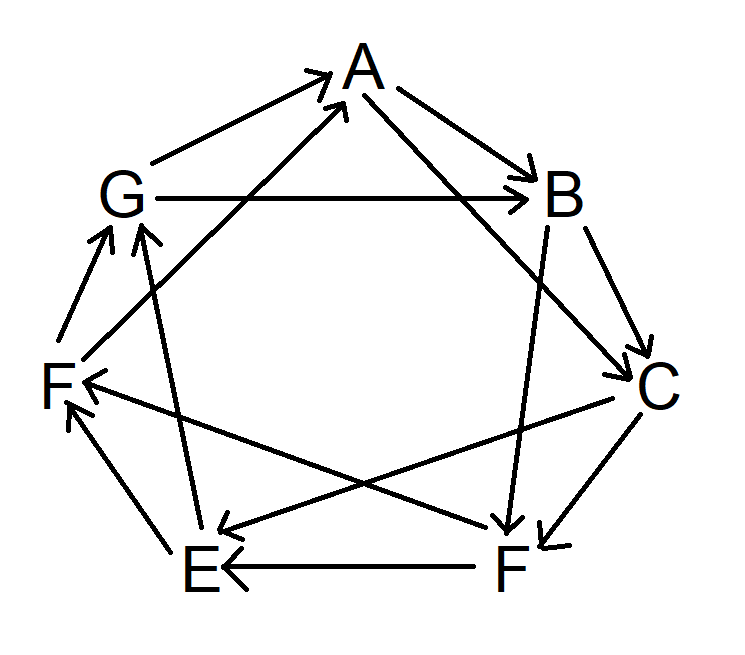
Наконец, проделайте то же самое, но пропустите три символа по часовой стрелке. Теперь диаграмма выглядит так:
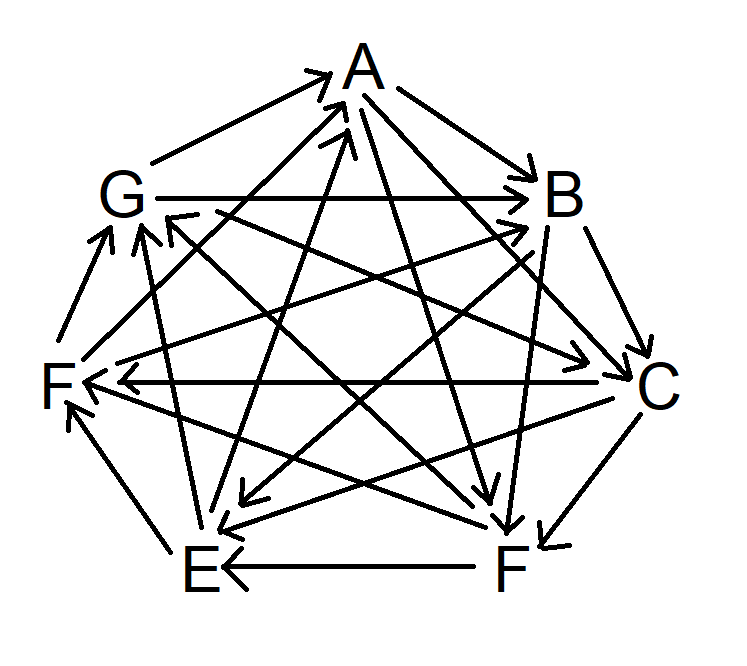
Обратите внимание, что на данном этапе каждый символ превосходит три других символа и проигрывает трем другим, отличающимся от него символам.
Этот метод будет работать для любого простого числа символов, потому что к тому моменту, когда вы вернетесь к исходному символу, вы пройдете через каждый символ. Для n символов вам придется пройти этот процесс (n-1)/2 раз.
Можно создать сбалансированную игру с любым нечетным количеством символов, но иногда цикл будет слишком быстро возвращаться к исходному символу. В этом случае придется создавать новые циклы, начиная с пропущенных символов.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Какова вероятность ничьей в игре «Три карты»?
Точный ответ: 450528/407170400 ≈ 0,001106485 ≈ 1/904.
В следующей таблице показано количество способов составить каждый тип начальной руки и количество комбинаций, которые дают ничью во второй раздаче. В случае стритов и «мусорных» рук имеет значение, представлены ли две или три масти в первой раздаче.
В нижней правой ячейке показано, что в трехкарточном покере существует 450 528 способов сыграть вничью. Общее количество комбинаций для двух рук равно combin(52,3)*combin(49,3) = 407170400. Таким образом, ответ равен 450528/407170400.
Ничья в покере на трёх картах
| Рука | Рука 1 | Рука 2 | Продукт |
|---|---|---|---|
| Три одинаковых | 52 | 0 | 0 |
| Прямой смыв | 48 | 3 | 144 |
| Стрит (три масти) | 288 | 26 | 7488 |
| Прямой бейдж (две масти) | 432 | 25 | 10,800 |
| Румянец | 1096 | 3 | 3288 |
| Пара | 3744 | 3 | 11,232 |
| Джэнк (три костюма) | 6,576 | 26 | 170,976 |
| Джонк (два костюма) | 9,864 | 25 | 246,600 |
| Общий | 22,100 | 450,528 |
Какова ценность купона на бесплатный туз в блэкджеке 6-5?
В описании бесплатной страницы с тузами я указываю, что ее ценность составляет 50,1844% от суммы ставки в блэкджеке 3-2.
В шестиколодном блэкджеке вероятность получения выигрышного блэкджека при наличии туза в качестве первой карты составляет 29,3139%. В этом случае вы выигрываете на 0,3 единицы меньше в блэкджеке 6-5, чем в блэкджеке 3-2.
Таким образом, стоимость бесплатного туза в шестиколодном блэкджеке 6-5 составляет 50,1844% × 29,3139 × 0,3 = 41,3902% от начальной ставки.
Кто-то предложил мне пари: он должен был выбросить в сумме 12 очков двумя кубиками за 27 бросков. Если бы он этого не сделал, я бы выиграл равную сумму. Поскольку вероятность выпадения 12 составляет 1/36, разве ему в среднем не потребовалось бы 36 бросков, чтобы выбросить 12? Казалось бы, шансы были бы на моей стороне, если бы мой противник выбрасывал всего 27 очков. Прав ли я или в чем ошибка в моих расчетах?
Среднее время ожидания между выпадением 12 действительно составляет 36 бросков, включая сам бросок на 12. Однако это не означает, что они выпадают ровно каждые 36 бросков. Вероятность того, что НЕ выпадет 12, составляет (35/36). Вероятность того, что этого не произойдет за 27 бросков, составляет (35/36)^27. Таким образом, вероятность того, что хотя бы один раз выпадет 12, составляет 1-(35/36)^27 = 53,26%.
В следующей таблице показана вероятность выпадения как минимум 12 чисел при 20-36 бросках. Обратите внимание, что для получения преимущества при равных шансах необходимо 25 выпадений.
Вероятность 12
| Роллы | Вероятность |
|---|---|
| 20 | 43,07% |
| 21 | 44,66% |
| 22 | 46,19% |
| 23 | 47,69% |
| 24 | 49,14% |
| 25 | 50,55% |
| 26 | 51,93% |
| 27 | 53,26% |
| 28 | 54,56% |
| 29 | 55,82% |
| 30 | 57,05% |
| 31 | 58,24% |
| 32 | 59,40% |
| 33 | 60,53% |
| 34 | 61,63% |
| 35 | 62,69% |
| 36 | 63,73% |


