Спросите Волшебника #395
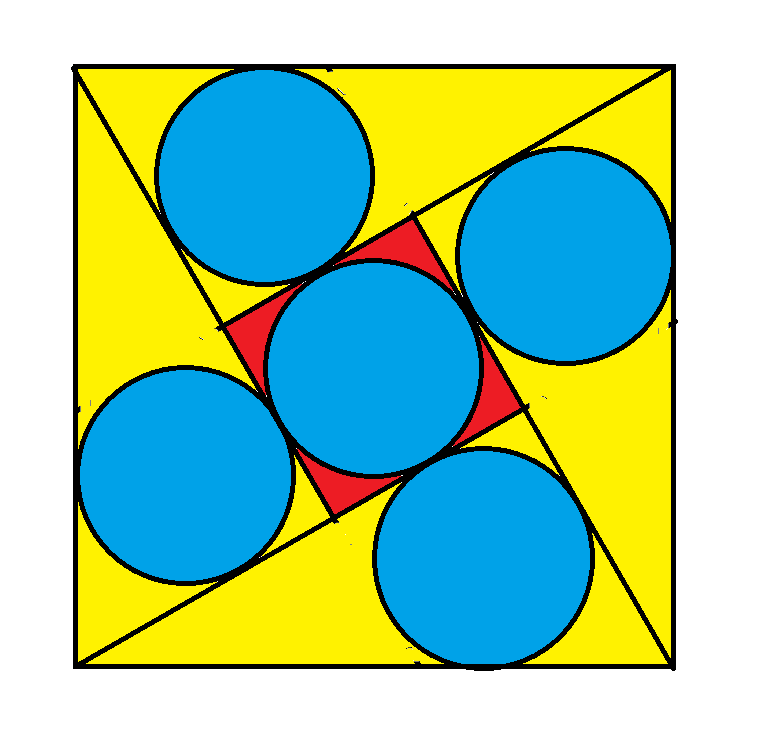
На приведенной выше диаграмме изображены четыре прямоугольных треугольника и маленький квадрат внутри большого квадрата. Длина стороны большого квадрата равна 1. Все пять окружностей имеют одинаковый диаметр. Каков этот радиус?
[спойлер=Ответ]
радиус = (sqrt(3)-1)/4 ≈ 0,183013.
[/спойлер] [spoiler=solution]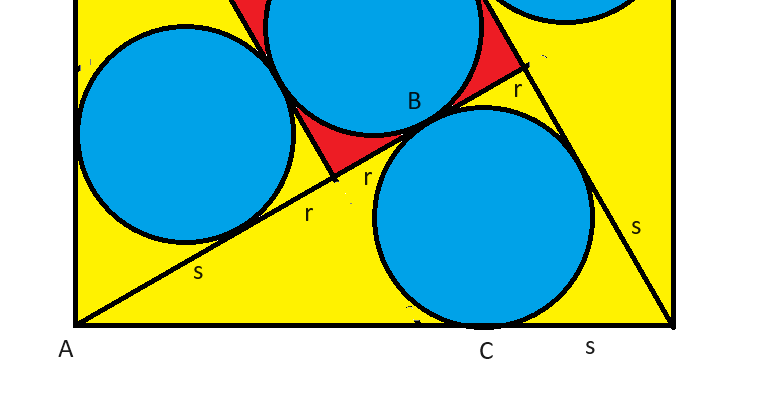 Рассмотрим один из треугольников. Дадим ему определение:
Рассмотрим один из треугольников. Дадим ему определение:- r = Радиус окружностей
- s = Расстояние между любым углом большого квадрата и точкой касания ближайшей окружности к треугольнику, в который он вписан.
Глядя на треугольник на изображении, расстояния между ними следующие:
- короткий конец = r+s
- длинная нога = 3r+s
- гипотенуза = 1
Используя формулу Пифагора:
(r+s) ² + (3r+s) ² = 1
r² + 2rs + s² + 9r² + 6rs + s² = 1
10r² + 2s² + 8rs = 1
Для решения нам понадобится другое уравнение. Давайте посмотрим на длину большого квадрата, которая, как нам дано, равна 1. AB = AC. AB = 2r + s, следовательно, AC = 2r + s. Остальная сторона большого квадрата равна s. Итак:
2r + 2s = 1.
2s = 1-2r
s = 1/2 - r
Давайте подставим это в наше уравнение, полученное с помощью формулы Питагора:
10r² + 2(1/2 - r) ² + 8r(1/2 - r) = 1
10р 2 + 2(1/4 - р + р 2 ) + 4р - 8р 2 = 1
2р 2 + 1/2 - 2р + 2р 2 + 4р = 1
4r² + 2r - 1/2 = 0
8r² + 4r - 1 = 0
Используя квадратное уравнение:
r = (-4 +/- sqrt(48))/16
r = (sqrt(3)-1)/4 =~ 0,183013.
Эта задача взята с YouTube-канала Mind Your Decisions . Преш предлагает решение, которое не требует использования формулы Пифагора.
[/спойлер]
Эта проблема задается и обсуждается на моем форуме Wizard of Vegas .
Каково ваше мнение о системе «Правильный и неправильный путь»? Суть в том, что игрок делает ставку «не пас» в размере одной единицы. Если выпадает какое-либо число, игрок ставит одну единицу на это число. Если число выпадает, игрок получает прибыль, а если выпадает семерка, он выходит в ноль. Это похоже на фриролл. Что я упускаю?
Допустим, если выпадает 4 или 10, игрок платит 5% комиссии только с выигрыша. Будем следовать правилу Вегаса, где 12 на первом броске считается ничьей по ставке «не пас» (в северной Неваде ничья при выпадении 2). Итак, вот все возможные исходы:
- Выпадение 2 или 3 на броске кубика: игрок выигрывает одну единицу по ставке «не пасуй».
- Выпадение 12 на броске кубика: игрок ставит на "не пас".
- Если выпадет 7 или 11, игрок проигрывает по ставке «не пасуй».
- Выигрыш по очкам 4 или 10: игрок выигрывает 1,95 единицы на ставке «купить» и проигрывает одну единицу на ставке «не пройти», чистый выигрыш составляет 0,95 единицы.
- Ставка в 5 или 9 очков приносит выигрыш: игрок выигрывает 1,4 единицы по ставке на место и проигрывает одну единицу по ставке «не проходит», чистый выигрыш составляет 0,4 единицы.
- Выпадение 6 или 8 очков и выигрыш по очкам: игрок выигрывает 7/6 единиц по ставке на место и проигрывает одну единицу по ставке «не проходит», чистый выигрыш составляет 1/6 единиц.
- Если набрано 4 или 10 очков, игрок проигрывает: он теряет 1 единицу на ставке покупки и выигрывает 1 единицу на ставке «не пасует» для чистого выигрыша.
- Если выпадает 5 или 9 очков и очко проигрывается: игрок теряет 1 единицу по ставке на место и выигрывает 1 единицу по ставке «не пасует» для чистого выигрыша.
- Если набрано 6 или 8 очков и очко проиграно: игрок теряет 1 единицу на ставке на место и выигрывает 1 единицу на ставке «не пасует» для чистого выигрыша.
В следующей таблице приведены все возможные исходы. В таблице показана вероятность, выигрыш и вклад в прибыль для всех возможных исходов. В нижней правой ячейке указан ожидаемый убыток в размере 0,02951 единиц.
Система правильного и неправильного пути
| Событие | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| Выходите по 2 или 3 человека | 1 | 0.083333 | 0.083333 |
| Выходите в 12 | 0 | 0.027778 | 0.000000 |
| Выходите в 7 или 11 | -1 | 0.222222 | -0.222222 |
| Победа с результатом 4 очка | 0,95 | 0.027778 | 0.026389 |
| Победа с результатом 5 очков | 0,4 | 0.044444 | 0.017778 |
| Победа с результатом 6 очков | 0.166667 | 0.063131 | 0.010522 |
| Победа с результатом 8 очков | 0.166667 | 0.063131 | 0.010522 |
| Победа Point 9 | 0,4 | 0.044444 | 0.017778 |
| Победа с 10 очками | 0,95 | 0.027778 | 0.026389 |
| Поражение с результатом 4 очка | 0 | 0.055556 | 0.000000 |
| Поражение в 5 очков | 0 | 0.066667 | 0.000000 |
| Поражение с результатом 6 очков | 0 | 0.075758 | 0.000000 |
| Поражение с результатом 8 очков | 0 | 0.075758 | 0.000000 |
| Поражение с результатом 9 очков | 0 | 0.066667 | 0.000000 |
| Поражение с разницей в 10 очков | 0 | 0.055556 | 0.000000 |
| Общий | 1.000000 | -0.029512 |
Причина отрицательного ожидаемого значения этой стратегии кроется в первом броске кубика. При выпадении 2 или 3 есть 3 способа выиграть, а при выпадении 7 или 11 — 8 способов проиграть. Действительно, если игрок переживает первый бросок, у него положительное эквити, но этого недостаточно, чтобы компенсировать ожидаемый проигрыш при первом броске.
Моя жена злится в 20% случаев. На вопрос «Ты злишься?» она отвечает «нет» в 90% случаев, когда злится. На тот же вопрос, когда она не злится, она отвечает «нет» в 95% случаев. Мой вопрос: какова вероятность того, что она злится, в зависимости от ответа на этот вопрос?
Это классический вопрос байесовской теории вероятностей.
[спойлер=Ответ]Если она ответит «нет», вероятность того, что она сошла с ума, составляет 9/47 = 19,15%.
Если она ответит «да», то вероятность того, что она сошла с ума, составит 1/3 = 33,33%.
[/спойлер] [spoiler=Решение]Формула для ответа на вопросы, сформулированные как «если А, то В», — это вероятность (и А, и В) / вероятность (В).
В случае отрицательного ответа вероятность того, что она рассержена, составляет (0,2*0,9)/(0,2*0,9 + 0,8*0,95) = 0,18/0,94 = 9/47.
В случае положительного ответа вероятность того, что она недовольна, составляет (0,2*0,1)/(0,2*0,1 + 0,8*0,05) = 0,02/0,06 = 1/3.
[/спойлер]

