Спросите Волшебника #399
Если убрать маленький квадрат с первого изображения и переставить части, общая площадь, кажется, останется той же. Как это возможно?
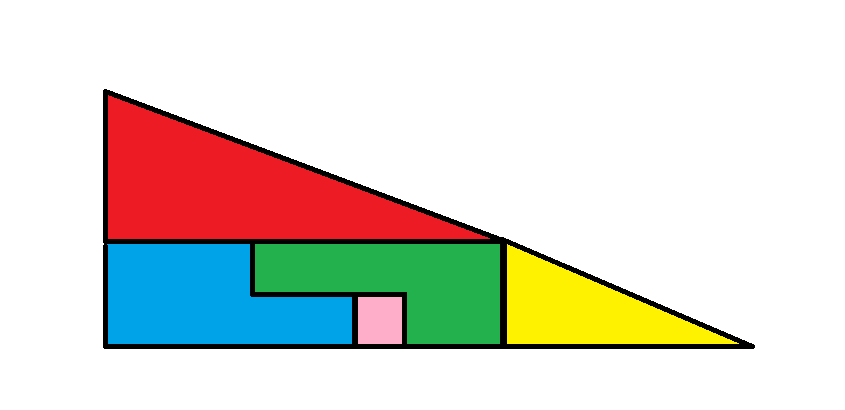
Изображение 1
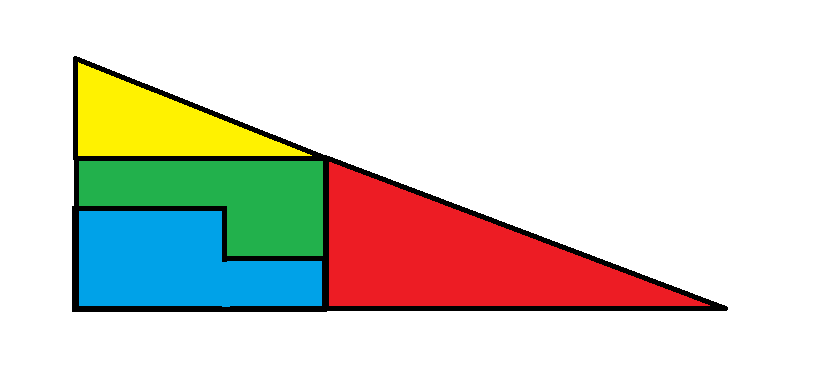
Изображение 2
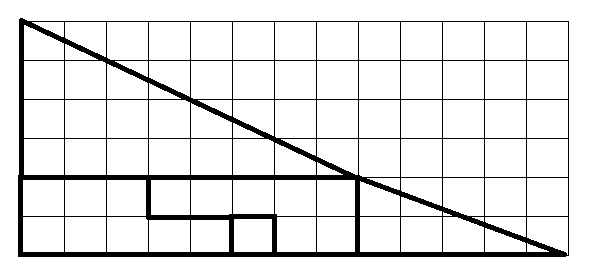
На изображении выше показано первое изображение, расположенное на сетке, чтобы лучше оценить размер каждого элемента.
Обратите внимание, что у большого красного треугольника стороны равны 4 и 8. Затем обратите внимание, что у меньшего желтого треугольника стороны равны 2 и 5. Другими словами, треугольники не пропорциональны. Гипотенузы двух треугольников имеют разные наклоны, как показано на рисунках. У одного наклон равен 0,5, а у другого — 0,4. Если расположить детали так, как показано на рисунках, может показаться, что они образуют большой треугольник со сторонами 5 и 13, но это не треугольник.
Площадь красного треугольника равна 4*8/2 = 16.
Площадь жёлтого треугольника равна 2*5/2 = 5.
На первом изображении остальные три части образуют прямоугольник размером 2 на 8, общей площадью 16.
На втором изображении два других фрагмента образуют прямоугольник размером 3 на 5, общей площадью 15.
Общая площадь первого изображения равна: красный треугольник + желтый треугольник + большой прямоугольник = 16 + 5 + 16 = 37.
Общая площадь второго изображения равна: красный треугольник + желтый треугольник + маленький прямоугольник = 16 + 5 + 15 = 36.
В заключение, первое изображение больше с маленьким квадратом. Это оптическая иллюзия, что все части вместе образуют большой треугольник в обоих случаях. На самом деле это не так.
На краю большой пустыни находятся 16 мотоциклов. Каждый мотоцикл может проехать 100 миль на одном баке бензина. Все мотоциклы начинают с полным баком. Пересадка между мотоциклами разрешена. Цель — доставить один мотоцикл как можно дальше от начальной точки. Как далеко он сможет проехать?
Суть проблемы в том, чтобы группа проехала небольшое расстояние. Затем взяла оставшийся бензин с одного из мотоциклов и заправила баки остальных.
Например, в начале разделите полный бак бензина на 16 частей, по одной на каждый мотоцикл. Затем все едут вместе, пока не израсходуется 1/16 бака, что составит 100/16 = 6,25 миль. Возьмите 15/16 бака из одного мотоцикла и перелейте 1/16 бака в остальные 15 мотоциклов, что точно заправит их до полного бака.
Затем повторите тот же процесс, но, имея в наличии 15 мотоциклов, проедьте столько, сколько хватит 1/15 бака, то есть 100/15 = 6,666667 миль. Затем возьмите еще 14/15 бака с одного мотоцикла и перелейте 1/15 бака в остальные 14 мотоциклов.
Продолжая этот процесс, последний мотоцикл преодолеет расстояние, равное (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338,072899 миль.
[/спойлер]Этот вопрос был задан и обсуждался на моём форуме, посвящённом игре Wizard of Vegas .
Что вы думаете о парадоксе Спящей красавицы?
Для удобства других читателей, вот что спрашивается в «Проблеме/парадоксе Спящей красавицы».
Спящая красавица добровольно соглашается на эксперимент. Ей правдиво объясняют все детали эксперимента, а именно:
- Воскресенье: СБ усыпляют. После того, как она заснет, подбросят честную монету.
- Понедельник: В понедельник СБ разбудят и спросят: «Какова вероятность того, что монета выпала орлом?» После того, как она ответит, её снова усыпят с помощью препарата от амнезии, который заставит её забыть всё, что произошло в понедельник.
- Вторник: Если монета выпадет решкой, повторится то же самое, что и в понедельник. Если же выпадет орлом, она проспит весь день.
- Среда: СБ снова будят, ничего не спрашивают, и он уходит домой, так как эксперимент окончен.
Вопрос в том, как ей следует ответить на вопрос, заданный в понедельник, а возможно, и во вторник?
Мой ответ
Если бы этот эксперимент повторили миллионы раз, мы могли бы ожидать увидеть три типа пробуждений, каждый из которых был бы одинаково вероятен:
- Монета выпала орлом вниз и проснулась в понедельник.
- Монета выпадет решкой, и в понедельник она проснётся.
- Монета выпадет решкой, и очнётся во вторник.
Это объясняется тем, что количество пробуждений в понедельник должно быть поровну распределено между подбрасываниями монеты (орлом и решкой). Кроме того, если монета выпадет решкой, то количество пробуждений в понедельник и вторник будет абсолютно одинаковым. Таким образом, во всех трех группах будет примерно одинаковое количество пробуждений при большом объеме выборки.
Из этих пробуждений одно из трех происходит после подбрасывания орла. Таким образом, вероятность выпадения орла составляет 1/3.
Сторонники теории 1/2 утверждают, что SB не получает никакой дополнительной информации при каждом пробуждении и, следовательно, следует предполагать, что каждый исход переворота был одинаково вероятен.
К этому я бы расширил задачу до 999 999 пробуждений, если бы монета выпала решкой. Только 1 из миллиона пробуждений происходит после подбрасывания орла. Таким образом, довольно легко предположить, что любое пробуждение, вероятно, было одним из 999 999 пробуждений после выпадения решки. Другими словами, правильный ответ в этом случае будет 1 из 1 000 000.
В качестве еще одного примера, что если бы СБ попросили предсказать результат подбрасывания монеты при каждом пробуждении? Если бы она угадала правильно, она бы выиграла 1000 долларов. Если бы у нее была стратегия предсказывать «орёл», она могла бы рассчитывать на выигрыш (1/2) * 1000 долларов = 500 долларов. Если бы у нее была стратегия предсказывать «решка», она могла бы рассчитывать на выигрыш (1/2) * 2000 долларов = 1000 долларов. Таким образом, сам факт пробуждения СБ склоняет чашу весов в пользу выпадения решки.
Если моё объяснение было непонятным, то в Википедии проблема Спящей красавицы рассматривается гораздо подробнее, чем я, включая другие возможные ответы от Спящей красавицы.
Этот вопрос был задан и обсуждался на моём форуме, посвящённом игре Wizard of Vegas .


