Спросите Волшебника #405

Пусть y = обоим выражениям. Таким образом, получаем:

• y = x² - 3
• y = sqrt(x+3)

Обратите внимание на цифру 3 в обоих выражениях. Давайте выразим оба уравнения с цифрой 3 с одной стороны. Сначала получим:

3 = x² - y

Далее возведем в квадрат второе уравнение:

y² = x + 3

3 = y² - x

Давайте приравняем оба выражения к числу 3:

x² - y = y² - x

Давайте переставим:

x² - y² + x - y = 0

(x+y)(xy) + x - y = 0

(xy)(x+y+1) = 0

Для начала рассмотрим случай xy = 0:

xy = 0

Подставим y = x² - 3 вместо y.

x - (x^2 - 3) = 0

x² - x - 3 = 0

Используя формулу Пифагора:

x = (1 +/- sqrt(1 + 12)/2

x = (1 + sqrt(13)/2 & x = (1 - sqrt(13)/2

Во-вторых, рассмотрим случай x+y+1 = 0:

Подставим y = x² - 3 вместо y.

x + (x² - 3) + 1 = 0

x + x² - 3 + 1 = 0

x² + x - 2 = 0

Используя формулу Пифагора:

x = (-1 +/- sqrt(1 + 8)/2

x = (-1 +/- 3)/2

x = 1, x = -2

Итак, у нас есть четыре ответа:

• x = 1
• x = -2
• x = (1 + sqrt(13)/2 ≈ 2,302776
• x = (1 - sqrt(13)/2 ≈ -1,302776

Я хотел бы поблагодарить видео на YouTube от SyberMath «Решение уравнения x²-3=sqrt(x+3)», которое помогло мне найти этот способ решения. Перейдите к отметке 6:28, чтобы увидеть этот метод.

[spoiler=Решение] Рассмотрите эту диаграмму в качестве решения.

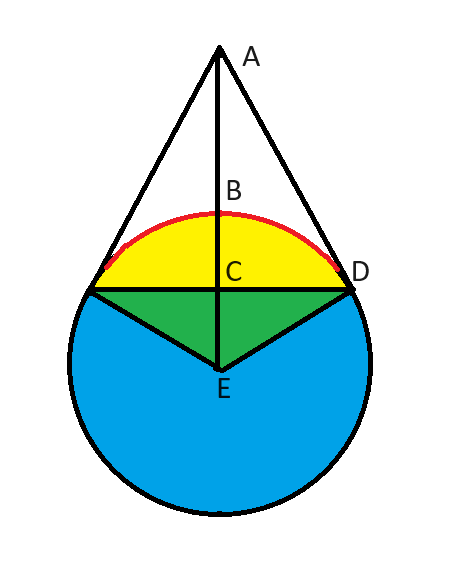
Рассмотрим треугольник ADE. Мы знаем:

• Угол ADE равен 90 градусам, потому что AD является касательной к окружности.
• Угол AED равен 60 градусам, потому что угол зеленого треугольника в точке E составляет 120 градусов (1/3 от общего угла в 360 градусов).
• Угол EAD должен быть равен остальным 30 градусам треугольника ADE.

Это классический треугольник 30-60-90. Всем известно, что стороны этого треугольника пропорциональны 1, 2 и sqrt(3).

В данном случае ED = 1, как указано в задании. AE вдвое больше этого расстояния, или 2.

2 — это расстояние от точки до центра окружности. Нас спрашивают о расстоянии от точки до ближайшей точки на окружности. Поэтому мы вычитаем радиус. Таким образом, ответ: 2 - 1 = 1.

[/спойлер]

Помните, что расстояние = скорость * время, что мы выразим как d = r*t

Перепишем это так: t = d/r.

Время встречи Боба и поезда в начале моста совпадает:

Давайте позволим:

• x = расстояние между начальным положением поезда и началом моста.
• r = скорость поезда

Сначала давайте посмотрим на Боба, который бежит обратно. Давайте обозначим точку t так, чтобы Боб и поезд встретились в начале моста:

Боб: t = (1/3)/5

Поезд: t = x/r

Приравнивая два выражения для t:

r/3 = 5x

r = 15x

Во-вторых, давайте посмотрим на Тома, который бежит впереди. Давайте обозначим точку t так, чтобы Том и поезд встретились в начале моста:

Том: t = (2/3)/5

Тренировка: t = (1+x)/r

Приравнивая два выражения для t:

(2/3)/5 = (1+x)/r

2r/3 = 5(1+x)

2r = 15(1+x)

2r = 15 + 15x

На данный момент у нас есть:

• r = 15x
• 2r = 15 + 15x

Подставим выражение для r из первого уравнения во второе:

30x = 15 + 15x

15x = 15

x = 1

Напомним, r = 15x.

Таким образом, скорость поезда составляет 15*1 = 15 миль в час.