WOO logo

Wizard рекомендует

Спросите Волшебника #407

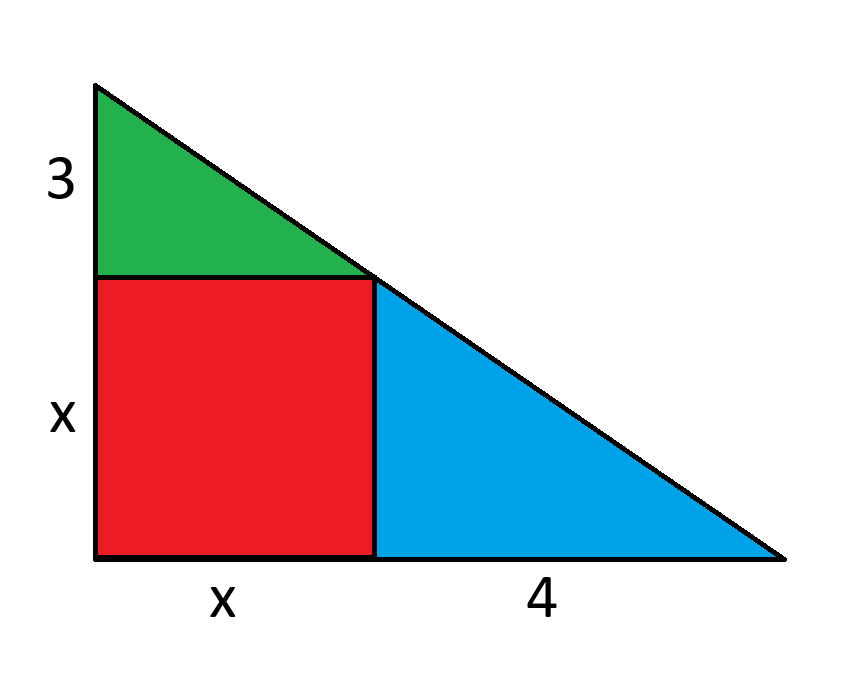
Найдите x.

анонимный

Давайте составим уравнение, сопоставляющее площадь отдельных частей треугольника со всей его площадью:

Зеленый + Синий + Красный = Итого
3x/2 + 4x/2 + x^2 = (x+3)*(x+4)/2
3x + 4x + 2x² = (x+3)*(x+4)
7x + 2x² = x² + 7x + 12
2x² = x² + 12 x² = 12 x = 2 * √3 ≈ 3,464102

Этот вопрос основан на аналогичном вопросе Преш Талкволкар с YouTube-канала "Mind Your Decisions", а именно на первой задаче в этом видео . Преш предлагает остроумное и отличное от моего решение.

Вы находитесь в оазисе в пустыне. Ваша задача — как можно быстрее доставить письмо на расстояние 100 миль. Ваш верблюд может перевозить запас воды на три дня и преодолевать 20 миль в день. Оставлять запасы воды в пустыне разрешено. Как быстро вы сможете доставить письмо?

анонимный

Нажав на следующую кнопку, вы увидите мой ответ. Он покажет мое лучшее время, но я не могу доказать, что нет лучшего способа.

11,8 дней

[spoiler=Решение]
  1. Совершите четыре поездки на аванпост, расположенный в 8 милях отсюда. За первые три поездки вы сможете доставить 44 галлона, а за четвертую — 52, в общей сложности 184 галлона. Это потребует 7*8=56 миль пешего пути, что займет 56/20 = 2,8 дня.
  2. Совершите три поездки на аванпост, расположенный в 12 милях от вас. В первых двух поездках вы сможете доставить 36 галлонов, а в третьей — 48, в общей сложности 120 галлонов. Это потребует 5*12=60 миль пешего пути, что займет 60/20 = 3,0 дня.
  3. Совершите две поездки на аванпост, расположенный в 20 милях отсюда. В первой поездке вы сможете доставить 20 галлонов, а во второй — еще 40, итого 60 галлонов. Это потребует 3*20=60 миль пешего пути, что займет 60/20 = 3,0 дня.
  4. Совершите одну поездку на аванпост, расположенный в 60 милях отсюда. Это потребует пройти 60 миль пешком, что займет 60/20 = 3,0 дня.

Расстояние до аванпоста составляет 8+12+20+60 = 100 миль. Общее необходимое время — 2,8 + 3,0 + 3,0 + 3,0 = 11,8 дней.

[/спойлер]

У вас есть бокал для мартини высотой 4 дюйма. Насколько высоко нужно его наполнить, чтобы налить половину полной порции?

анонимный

4×(1/2)^(1/3) = 3,174802 дюйма в высоту.

[spoiler=Решение]

Интересно, что радиус не имеет значения. Назовем радиус r. Назовем высоту, на которую бармен должен наполнить стакан, h. Очевидно, что радиус половины стакана равен соотношению радиусов двух предыдущих высот. Другими словами, радиус половины стакана равен r*(h/4).

Напомним, что объем конуса равен (1/3)*h*pi* r² .

Давайте приравняем половину порции к половине полной порции:

(1/2)*(1/3)*4*pi*r 2 = (1/3)*h*pi*(rh/4) 2

(1/2)*4*r 2 = h*(rh/4) 2

2* r² = h* r² * h² / 16

2 = h 3 /16

32 = h 3

h = 32 1/3 ≈ 3,174802"

[/спойлер]