Спросите Волшебника #410
Я вижу, вы ответили на вопрос об игре Плинко в рубрике «Спроси волшебника» программы «Цена правильная» № 115. Однако иногда размеры призов меняются для специальных выпусков. Например, в «Неделю больших денег» призы слева направо были следующими: 500, 1000, 2500, 0, 200000, 0, 2500, 1000, 500 долларов. Каково будет ожидаемое значение для каждой позиции, с которой бросается шайба? Какова вероятность того, что шайба попадёт в любую заданную призовую позицию при любой заданной начальной позиции?
Существует девять стартовых позиций для бросания шайбы. Однако нас интересуют только пять, поскольку призы и расположение колышков симметричны. Давайте обозначим их, начиная с левого края, от 1 до 5.
Существует также девять конечных позиций, давайте обозначим первые пять, начиная слева, цифрами от 1 до 5.

В следующей таблице показана вероятность попадания в любую заданную точку (левый столбец) в зависимости от места, откуда был сброшен снаряд (верхняя строка).
| Место посадки | Сбросить 1 или 9 | Сбросить 2 или 8 | Сбросить 3 или 7 | Уберите 4 или 6 | Сброс 5 |
|---|---|---|---|---|---|
| 1 или 9 | 0.225586 | 0.193359 | 0.121094 | 0.056641 | 0.032227 |
| 2 или 8 | 0.386719 | 0.346680 | 0.250000 | 0.153320 | 0.113281 |
| 3 или 7 | 0.242188 | 0.250000 | 0.257813 | 0.250000 | 0.242188 |
| 4 или 6 | 0.113281 | 0.153320 | 0.250000 | 0.346680 | 0.386719 |
| 5 | 0.032227 | 0.056641 | 0.121094 | 0.193359 | 0.225586 |
| Общий | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
В следующей таблице показана ожидаемая стоимость каждой позиции для выбранного вами варианта в рамках «Недели больших денег», о которой вы спрашивали. Как и ожидалось, игрок должен выбрать направление падения шайбы, превышающее самый крупный приз.
| Место высадки | Ожидаемая победа |
|---|---|
| 1 или 9 | 7 550,29 долларов США |
| 2 или 8 | 12 396,48 долларов США |
| 3 или 7 | 25 173,83 долл. США |
| 4 или 6 | 39 478,52 долл. США |
| 5 | 45 852,05 долларов США |
В чём заключается парадокс рога Габриэля?
Сначала рассмотрим кривую, полученную по уравнению y=1/x для значений x от 1 до бесконечности. График будет выглядеть следующим образом для значений x до 17.
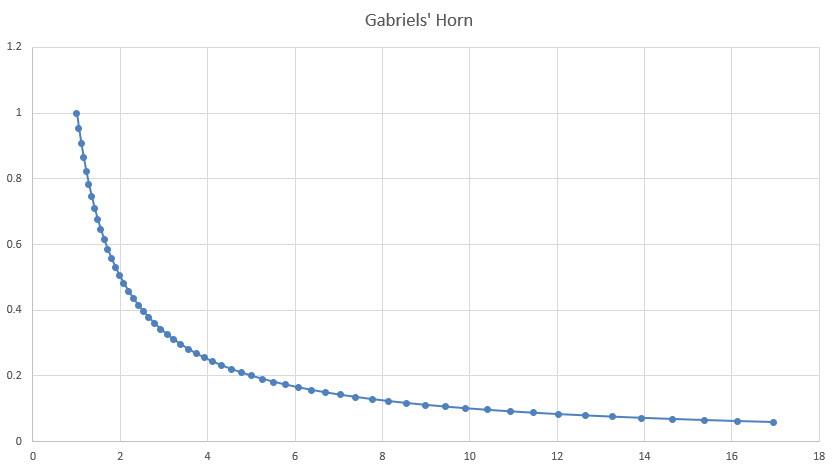
Далее представьте, что эта кривая вращается вокруг оси x. В результате получится нечто похожее на рог с бесконечно длинным концом. Это то, что математики называют рогом Габриэля?

Источник изображения: Soul of Mathematics .
Далее рассмотрим вопросы, касающиеся Рога Гавриила:
- Какой объём?
- Какова площадь поверхности?
Вот ответы:
[спойлер=Ответ]- Объём = π = пи.
- Площадь поверхности = бесконечность
С результатами моих исследований можно ознакомиться здесь (PDF).
Суть парадокса заключается в вопросе: как может объем быть конечным, а площадь поверхности — бесконечной?
Парадокс возникает, когда мы путаем два измерения с тремя. Так делать не следует. Рассмотрим окружность А радиусом 1 и окружность В радиусом 1,1, причем окружность А находится внутри окружности В.
Окружность А имеет длину окружности 2*π ≈ 6,283185, а окружность В имеет площадь 1,1²*π ≈ 3,801327. Обратите внимание, что окружность В больше окружности А, но её площадь меньше длины окружности В. Это не означает, что длина окружности В является частью площади А. Площадь и длина окружности — это разные измерения в разных измерениях, и их не следует сравнивать.
Иными словами, если бы мы сделали пластинку из круга А с бесконечным числом канавок, то длина этих канавок была бы бесконечной.
Возвращаясь к Рогу Габриэля, давайте упростим его до дискретного случая окружностей с радиусами 1, 1/2, 1/3, 1/4...
Сумма объемов этих кругов будет равна π*(1/1 + 1/4 + 1/9 + 1/16 + ...). Существует известный бесконечный ряд, который гласит:
1/1 + 1/4 + 1/9 + 1/16 + ... = π²/6 ≈ 1,644934.
Добавив еще один член с числом пи, получаем сумму площадей кругов π³/6 ≈ 5,167713.
Между тем, сумма длин окружностей равна 2*пи(1/1 + 1/2 + 1/3 + 1/4 + ...).
В математике существует еще один хорошо известный бесконечный ряд, называемый гармоническим рядом, который гласит:
1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = бесконечность.
2π∞ по-прежнему равно ∞.
Если мы распространим эту логику на бесконечно малые расстояния между окружностями, то получим Рог Габриэля.
Натан покупает 100 фунтов фасоли. Фасоль на 99% состоит из воды по весу. Она оставляет её на солнце, чтобы она высохла. На следующий день она обнаруживает, что фасоль на 98% состоит из воды. Каков будет её новый вес?
Позволять:
- w = Первоначальный вес воды.
- w' = Вес воды после высушивания бобов.
- x = Вес всего остального содержимого бобов.
Нам дано на первый день:
w + x = 100
w/(w+x) = 0,99
Подставляя первое уравнение во второе:
w/100 = 0,99
w = 99
Таким образом, x=1.
На следующий день нам предоставляется:
w'/(w'+x) = 0,98
w' = 0,98*(w'+x)
0,02w' = 0,98x
Мы знаем, что x=1, поэтому:
0,02w' = 0,98
w' = 0,98/0,02 = 49
Общий вес на следующий день составит x + w' = 1 + 49 = 50.
[/спойлер]


