WOO logo

Wizard рекомендует

Спросите Волшебника #413

Существует ли способ организовать обмен подарками в рамках «Тайного Санты», отвечающий следующим требованиям:

  • Никто не дарит себе подарки.
  • Изменений не будет.
  • Никто ничего не знает, кроме того, для кого они должны покупать.
  • Вероятность исхода каждого матча одинакова.

анонимный

Да! Я называю это методом Ханны Фрай.

  • Создайте набор карточек, как показано ниже. На каждой карточке должен быть уникальный номер сверху и снизу. В приведенном ниже примере номер равен 23.
  • Перетасуйте карты и сложите их заново.
  • Сохраняя стопку целой, разрежьте каждую карту по линии движения посередине, получив две стопки.
  • Разрежьте и завершите разрезание ОДНОЙ из стопок.
  • Раздайте каждому участнику по одной верхней карте из каждой стопки.
  • Составьте нумерованный список и попросите каждого написать в нем свой номер.

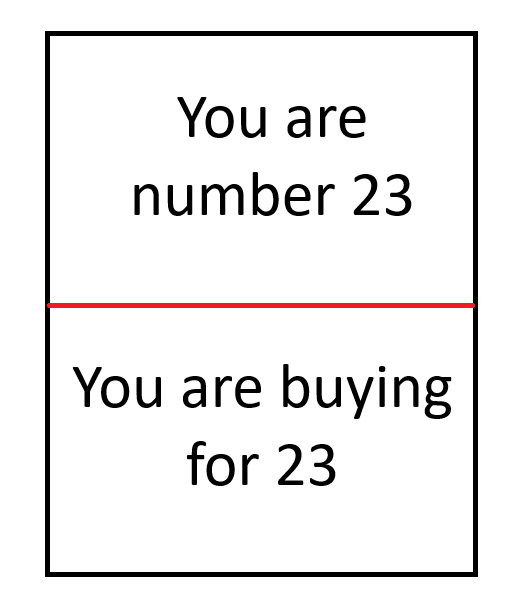
После выполнения этой процедуры у каждого будет две карточки с надписями, например, «Вы номер 13» и «Вы покупаете для номера 7». Как только список будет заполнен, каждый будет знать, для кого покупать, но не будет иметь ни малейшего представления о том, кто покупает для него.

Источник: Проблемы с «Тайным Сантой» — Numberphile .

Бассейн наполнен соленой водой. В бассейне содержится 1000 кубических метров воды. Садовый шланг подает в бассейн пресную воду со скоростью один кубический метр в час. По мере притока пресной воды, вода вытекает с того же конца с той же скоростью. Сколько времени потребуется, чтобы в бассейне осталось всего 1% соленой воды?

анонимный

Ответ: 2000 ln(10) ≈ 4605,170186 часов ≈ 191,8821 дня.

Вот моё решение (PDF).

В среднем, сколько оборотов требуется для каждого из платоновых тел, чтобы перевернуть любую из ранее перевернутых сторон?


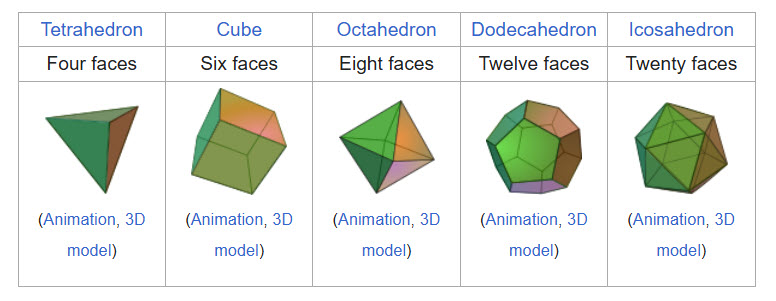
Источник изображения: Википедия

анонимный

Вот ответ, представленный в виде количества сторон.

Стороны Среднее количество рулонов
4 3.218750
6 3.774691
8 3.846558
12 5.036074
20 6.293585

Давайте рассмотрим только случай шестигранного куба.

  • Вероятность того, что эксперимент закончится двумя бросками кубиков, составляет 1/6.
  • Вероятность того, что эксперимент закончится тремя бросками кубиков, составляет (5/6)*(2/6).
  • Вероятность того, что эксперимент закончится четырьмя бросками кубиков, составляет (5/6)*(4/6)*(3/6).
  • Вероятность того, что эксперимент закончится пятью бросками, составляет (5/6)*(4/6)*(3/6)*(4/6).
  • Вероятность того, что эксперимент закончится шестью бросками, составляет (5/6)*(4/6)*(3/6)*(2/6)*(5/6).
  • Вероятность того, что эксперимент закончится семью бросками, составляет (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6).

Пусть pr(n) = вероятность того, что эксперимент закончится n бросками.

Ожидаемое значение броска: 2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =

2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3.774691358.