WOO logo

Wizard рекомендует

Спросите Волшебника #415

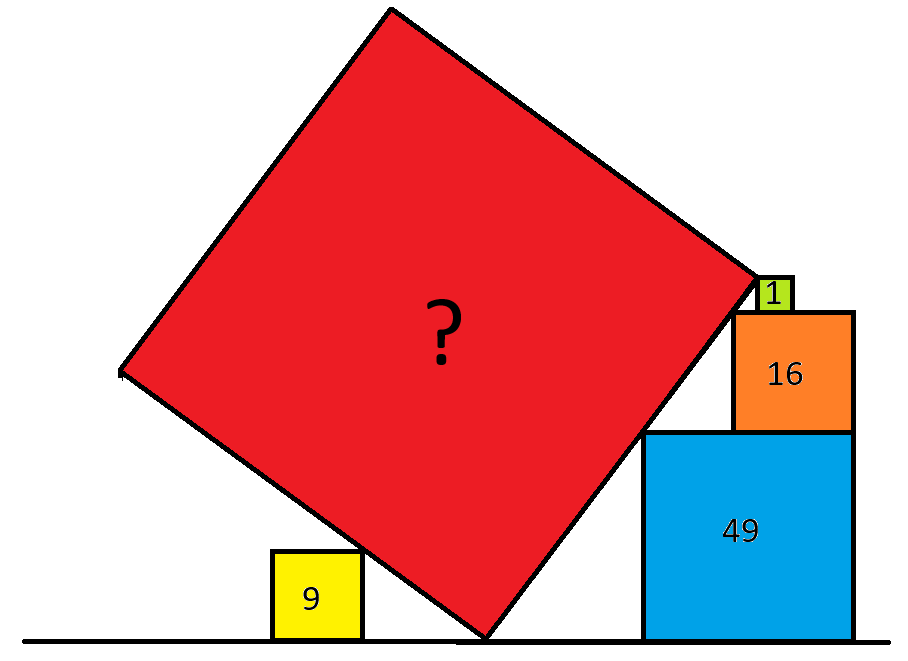
На изображении выше числа обозначают площади четырех квадратов. Какова площадь красного квадрата?

анонимный

225

[spoiler=Решение]

Во-первых, жёлтый квадрат нам ничем не помогает. Это отвлекающий манёвр, поэтому давайте его проигнорируем.

Далее рассмотрим треугольник слева от оранжевого квадрата, как показано на следующем изображении.

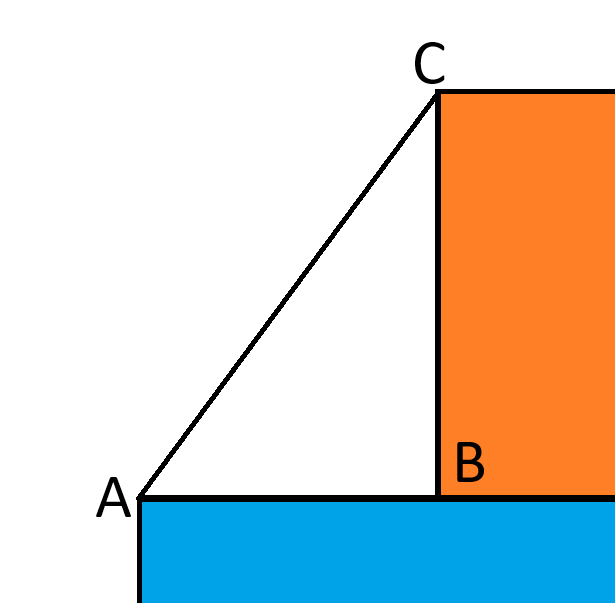
BC = sqrt(16) = 4.

AB = sqrt(49) - sqrt(16) = 7-4 = 3.

По формуле Пифагора, AC² = 4² + 3² = 25.

AC = sqrt(25) = 5.

Высота всех трех квадратов справа равна sqrt(49) + sqrt(16) + sqrt(1) = 12.

Отношение длины стороны красного квадрата к высоте трех квадратов справа будет таким же, как отношение AC к BC = 5/4.

Таким образом, длина стороны красного квадрата равна (5/4)*12 = 15.

Таким образом, площадь красного квадрата равна 15² = 225.

Похожая головоломка задается и обсуждается на моем форуме Wizard of Vegas .

На YouTube-канале Mind Your Decisions также есть похожая головоломка.

[/спойлер]

Какой наименьший возможный прямоугольник имеет площадь, равную периметру?

анонимный

Размеры прямоугольника 4х4, площадь и периметр 16.

[spoiler=Решение]

Пусть размеры прямоугольника равны x и y.

Нам дано: xy = 2x + 2y.
2y - xy = 2x
y(2-x) = 2x
y = 2x/(2-x)

Пусть f(x) = Площадь прямоугольника = x*y =
x*2x/(2-x) = 2x² /(2-x)

Чтобы найти минимальную площадь, возьмите производную, используя правило частного:

f'(x) = 4x(2-x) + 2x² / (2-x) ² = 0

4x(2-x) + 2x² = 0

8x = 2x 2

x=4

Если x=4, то y = 2*4/(4-2) = 8/2 = 4.

Давайте решим уравнение относительно y для других значений x, близких к 4.

Если x=3, то y=6, что соответствует площади 18.

Если x=5, то y = 10/3, что соответствует площади 16+(2/3).

Легко заметить, что решение при x=4 и y=4 приводит к минимуму. Таким образом, наименьший возможный прямоугольник равен 4х4 = 16.

[/спойлер]

В лотерее казино в барабане находится следующее количество билетов, принадлежащих владельцу билетов:

  • У игрока 1 6 билетов.
  • У игрока 2 2 билета.
  • У игрока 3 1 билет.
  • У 21 другого игрока есть 21 билет.

Казино разыграет пять билетов, на которые будут разыграны пять равных призов. Каждый игрок может выиграть только один раз. Если билет выпадет игроку, который уже выиграл, этот билет будет выброшен, и будет вытянут новый билет.

Игроки 1, 2 и 3 договариваются разделить выигрыш в соответствии со своей долей в розыгрыше. Какое разделение будет справедливым?

Mukke

Я упрощу задачу, предположив, что если билет выпадает игроку, который уже выиграл, то этот приз аннулируется. В противном случае, вычисления становятся слишком сложными и практически требуют случайной симуляции.

Вероятность того, что игрок, имеющий n билетов, НЕ выиграет приз, равна combin(30-n,5)/combin(30,n).

Таким образом, вероятность того, что игрок А выиграет приз, составляет 1-комбинация(24,5)/комбинация(30,5) = 0,701739.

Таким образом, вероятность того, что игрок B выиграет приз, составляет 1-комбинация(28,5)/комбинация(30,5) = 0,310345.

Таким образом, вероятность того, что игрок C выиграет приз, составляет 1-комбинация(29,5)/комбинация(30,5) = 0,166667.

Сумма этих вероятностей составляет 1,178750. Именно столько побед может одержать группа.

На мой взгляд, каждый игрок должен получить долю, равную его вероятности выигрыша приза, деленной на ожидаемое общее количество выигрышей группы.

А получает долю в размере 0,701739/1,178750 = 0,595324.

B получает долю в размере 0,310345/1,178750 = 0,263283.

C получает долю в размере 0,166667/1,178750 = 0,141393.

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .