WOO logo

Wizard рекомендует

Спросите Волшебника #418


Источник изображения: YouTube

Во втором сезоне игры «The Squid Game» представлена игра под названием «Камень, ножницы, бумага, минус один», правила которой объясняются в этом видео . Правила основаны на классической версии игры «Камень, ножницы, бумага» с учетом следующих изменений.

  • Одновременно оба игрока выкладывают по два символа, по одному на каждую руку.
  • После осмотра брошенного предмета оба игрока на счет три забирают по одному символу из одной руки, оставляя другую руку свободной.
  • Игра подсчитывается по стандартным правилам: камень побеждает ножницы, бумага побеждает камень, ножницы побеждают бумагу.

В видеоролике на YouTube рекрутер приводит в качестве примера следующую ситуацию:

  • Треугольник играет в ножницы и бумагу.
  • Circle играет в камень и бумагу

Рекрутер говорит, что Треугольнику следует сыграть в бумагу, потому что он не может проиграть. Правильна ли эта стратегия? Я склонен думать, что Круг, вероятно, предугадал бы эту стратегию и тоже попытался бы сыграть в бумагу, чтобы добиться ничьей. Таким образом, Треугольнику, возможно, следует хотя бы рискнуть и сыграть в ножницы. Какова оптимальная стратегия для обоих игроков?

анонимный

После проведения некоторых вычислений я пришел к выводу, что оптимальная стратегия для обеих сторон выглядит следующим образом:

  • Треугольник: бумага с вероятностью 2/3, ножницы с вероятностью 1/3.
  • Круг: бумага с вероятностью 2/3, камень с вероятностью 1/3.

Если хотя бы один игрок будет следовать этой стратегии, то вероятность каждого исхода для треугольника будет следующей:

  • Победа = 4/9
  • Ничья = 4/9
  • Убыток = 1/9

В случае с Circle ситуация обратная, а именно:

  • Победа = 1/9
  • Ничья = 4/9
  • Убыток = 4/9

В итоге, совет рекрутера абсолютно неверен. Вот мой общий совет на любой случай:

  • Всегда начинайте с двух разных символов.
  • Если вы выкладываете те же два символа, что и ваш противник, выложите тот символ, который победит другой выложенный вами символ. Например, если оба игрока выкладывают камень и бумагу, то выложите бумагу.
  • Если оба игрока выкладывают один общий символ, то с вероятностью 2/3 обе стороны должны выложить именно этот общий символ, а другая — с вероятностью 1/3.

Ссылки

Каково ожидаемое количество бросков, необходимых для того, чтобы одна и та же сторона шестигранной игральной кости выпала дважды? А как насчет других платоновых тел? Существует ли формула для любой n-гранной игральной кости?

анонимный

Результат броска шестигранной игральной кости: 1223/324 ≈ 3,774691 бросков.

В следующей таблице представлены ответы для различных количеств сторон.

Стороны Ожидал
Роллы
4 3.218750
6 3.774691
8 4.245018
12 5.036074
20 6.293585
50 9.543127
100 13.209961
200 18.398444

Вот формула для шестигранной игральной кости. Для любой другой игральной кости замените 6 на желаемое количество граней.

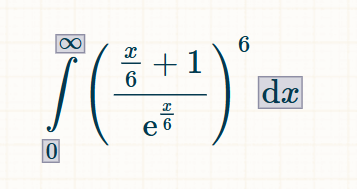
Для решения таких сложных интегралов я рекомендую сайт integral-calculator.com .

Выражаю благодарность участнику форума Wizard of Vegas Ace2 за помощь в решении этого вопроса.

Предположим, вам предоставляется возможность бросать игральную кость до тех пор, пока не выпадет 6. Выиграете сумму, равную количеству необходимых бросков в долларах. Например, если потребуется 6 бросков, вы выиграете 25 долларов. Каков ожидаемый выигрыш в этой игре?

анонимный

$66

Вот моё решение (PDF).