Спросите Волшебника #419
Я заметил, что у вас нет стратегий для видеопокера с более высоким выигрышем за последовательный роял. Можете мне помочь с этим?
Для начала позвольте мне пояснить некоторые термины, используемые в видеопокере.
- Последовательный роял = только от низкого к высокому (10-JQKA)
- Реверсивная королевская сетка = В обоих направлениях (10-JQKA или AKQJ-10)
Чтобы еще больше запутать ситуацию, не все используют эту терминологию, и в игре, где есть отдельная строка для последовательного роял-орла, оплата может производиться в обе стороны. Надеюсь, правила игры это прояснят.
Тем не менее, самый простой и идеальный способ разыграть руку, в которой возможен последовательный или обратный роял-карточный выигрыш, — это ввести её в мой калькулятор для видеопокера. Вот ссылки:
Если вы не можете или не хотите использовать мой сайт у игрового автомата, обратите внимание, что здесь указаны средние выигрыши за роял-карту, когда реверсивная роял-карта выплачивается в размере 50 000 за ставку в 5 кредитов, в зависимости от количества карт, уже находящихся на игровых позициях.
- 4 к обратимой королевской монете = 10 000
- 3 к обратимой королевской семерке = 5400
- 2 к обратимой королевской монете = 2333
- 1 к обратимой королевской карте (средняя позиция) = 1567
- 1 к обратимой королевской позиции (не средней позиции) = 1183
- 0 до обратимой королевской монеты = 800
Для последовательных игр в королевскую колоду (с выплатами только от низких к высоким) используйте число 1183 независимо от позиции.
Используя эти данные, воспользуйтесь моим конструктором стратегий для видеопокера и создайте отдельную стратегию для каждого из этих средних выигрышей по роял-картам. Затем используйте эту стратегию на автомате в зависимости от того, сколько карт для роял-карт находятся в правильной позиции.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Компания Kellogg's выпустила новые сферические версии хлопьев Apple Jacks, Frosted Flakes и Krave, утверждая, что такая форма обеспечивает больше глазури. Более того, они заявляют: «Мы всё подсчитали». Правильно ли они всё рассчитали?

Нет!!! Нет, они неправильно посчитали. На самом деле, сфера — это ХУДШАЯ трехмерная форма, если они хотят максимизировать соотношение площади поверхности к объему.
Начнём с рассмотрения уравнений для вычисления площади поверхности, указанных на обратной стороне коробки.

Они правильно утверждают, что площадь поверхности сферы, или, как они, вероятно, назвали бы ее «дыркой в пончике», равна 4πr² , где r — радиус.
Однако они неверно указывают, что площадь поверхности тора, который они, вероятно, назвали бы пончиком, равна 2π²rR . На самом деле формула удвоенная, или 4π²rR . Пожалуйста, обратитесь к следующему изображению для получения информации о r и R.
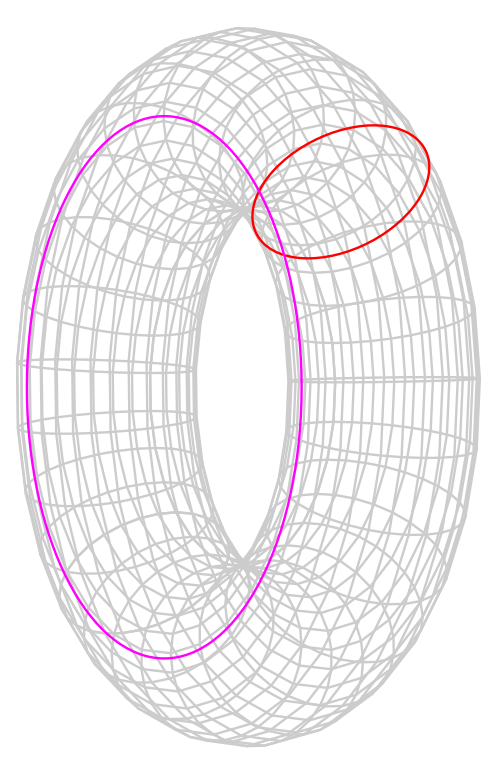
r = радиус красного круга
R = расстояние от ближайшей части тора до центра.
Источник изображения: страница Википедии о торе .
Можно сказать, что альтернативой сфере является нанесение глазури только на половину тора, как на пончик. Однако, внимательно изучив традиционный Apple Jacks в форме тора, я приведу пример: глазурь наносят на всю поверхность целиком.
Чтобы подкрепить свой следующий тезис, позвольте мне также привести формулы для объема сферы и тора.
- Сфера = (4/3) πr³
- Тор = 2π 2 r 2 R
Напомним, что формула для площади поверхности — это производная от объема.
Для тора с r=1 и R=1 мы получаем площадь поверхности 39,478418 и объем 19,739209. Интересно, что отношение площади поверхности к объему, или коэффициент глазури, равно ровно 2.
Чтобы уравнять объем, радиус сферы должен быть равен 1,676539. При таком радиусе сферы площадь поверхности составляет 35,321350, а объем — 19,739209. Отношение площади поверхности к объему, или коэффициент глазури, составляет 1,789400.
Иными словами, тор обеспечивает большую площадь поверхности или глазури при том же объеме.
Ранее я упоминал, что сфера — наихудшая трехмерная форма для выбора, если цель состоит в максимизации отношения площади поверхности к объему. Это известно как изопериметрическое неравенство . Хотя это и доказано, я думаю, это очевидно. Например, пузырьки стремятся минимизировать площадь поверхности и максимизировать прочность, и они имеют сферическую форму.
В итоге, если вы хотите свести к минимуму количество глазури, а не максимизировать его, вам следует выбирать хлопья Apple Jacks в форме шариков или пончиков. Это была бы моя цель, поскольку я считаю эти хлопья слишком сладкими и был бы рад меньшему количеству глазури. Я также категорически обвиняю Kellogg's в ложной рекламе, за что они заслуживают редкого для них позорного выговора.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Для получения дополнительной информации я рекомендую видео « Интернет обнаружил большую ошибку на коробке с хлопьями Kellogg's» на YouTube от Преш Талвалкар с канала MindYourDecisions (одно из моих любимых!).
Какова вероятность выигрышной комбинации в видеопокере?
Я понимаю, как ответ на этот вопрос может найти практическое применение в некоторых вариантах видеопокера, предлагающих бонусную функцию, если игрок получает выигрышную комбинацию.
Ответ зависит от формата видеопокера. В следующей таблице показано количество комбинаций и вероятность всех возможных событий при раздаче в видеопокере с колодой из 52 карт без джокеров, начиная с наименее оплачиваемой комбинации из пары валетов.
| Рука | Комбинации | Вероятность |
|---|---|---|
| Флеш-рояль | 4 | 0.000002 |
| Прямой смыв | 36 | 0.000014 |
| Четыре одинаковых | 624 | 0.000240 |
| Аншлаг | 3744 | 0.001441 |
| Румянец | 5108 | 0.001965 |
| Прямой | 10 200 | 0.003925 |
| Три одинаковых | 54,912 | 0.021128 |
| Две пары | 123,552 | 0.047539 |
| Валеты или лучше | 337,920 | 0.130021 |
| Все остальные | 2 062 860 | 0.793725 |
| Общий | 2 598 960 | 1.000000 |
Вероятность выигрышной комбинации в видеопокере Jacks or Better составляет 0,206275.
Во второй таблице показано количество комбинаций и вероятность всех возможных событий при раздаче в видеопокере с колодой из 52 карт, где двойки являются джокерами, начиная с самой низкооплачиваемой комбинации из трех одинаковых карт.
| Рука | Комбинации | Вероятность |
|---|---|---|
| Естественный королевский флус | 4 | 0.000002 |
| Четыре двойки | 48 | 0.000018 |
| Дикий роял флеш | 480 | 0.000185 |
| Пять одинаковых | 624 | 0.000240 |
| Прямой смыв | 2068 | 0.000796 |
| Четыре одинаковых | 31,552 | 0.012140 |
| Аншлаг | 12,672 | 0.004876 |
| Румянец | 14,472 | 0.005568 |
| Прямой | 62,232 | 0.023945 |
| Три одинаковых | 355,080 | 0.136624 |
| Все остальные | 2 119 728 | 0.815606 |
| Общий | 2 598 960 | 1.000000 |
Вероятность выигрышной комбинации в видеопокере Deuces Wild составляет 0,184394.
В третьей таблице показано количество комбинаций и вероятность всех возможных событий при раздаче в видеопокере с колодой из 53 карт, включая джокера, начиная с наименее оплачиваемой комбинации из пары королей.
| Рука | Комбинации | Вероятность |
|---|---|---|
| пять одинаковых | 13 | 0.000005 |
| Флеш-рояль | 24 | 0.000008 |
| прямой смыв | 180 | 0.000063 |
| четыре одинаковых | 3120 | 0.001087 |
| Аншлаг | 6,552 | 0.002283 |
| румянец | 7,804 | 0.002719 |
| прямой | 20,532 | 0.007155 |
| три одинаковых | 137,280 | 0.047838 |
| 2 пары | 123,552 | 0.043054 |
| Короли или лучше | 262,956 | 0.091632 |
| Все остальные | 2 307 672 | 0.804155 |
| Общий | 2 869 685 | 1.000000 |
Вероятность выигрышной комбинации в видеопокере с джокером (короли или лучше) составляет 0,195845.


