Спросите Волшебника #426
Предположим, что серийные номера нумеруются последовательно, начиная с 1. Максимальное количество номеров в обращении неизвестно. При случайной выборке из n номеров, какова наилучшая оценка максимального серийного номера?
Мне нравится представлять ответ так: нужно найти средний промежуток между порядковыми номерами. Для этого нужно взять максимальное значение и разделить его на размер выборки. Например, если самый большой элемент в вашей выборке равен 1000, а размер выборки — 5, то средний промежуток равен 1000/5 = 200. Затем добавьте этот промежуток к максимальному значению, чтобы получить приблизительное максимальное число. В этом примере 1000 + 200 = 1200.
Обычно используется формула, дающая тот же результат: M*(k+1)/k, где M = максимальное значение, а k = количество наблюдений. В нашем примере это дает 1000*(6/5) = 1200.
ABCD — квадрат со стороной длиной 10. Внутри него вписаны полукруг и четвертькруга, как показано на следующем рисунке.
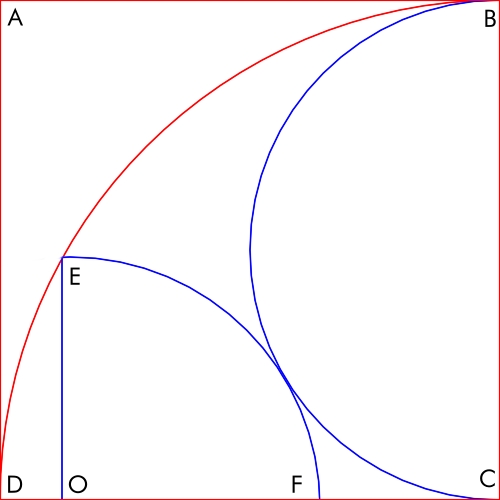
Какова длина OE?
Рассмотрим следующую диаграмму.
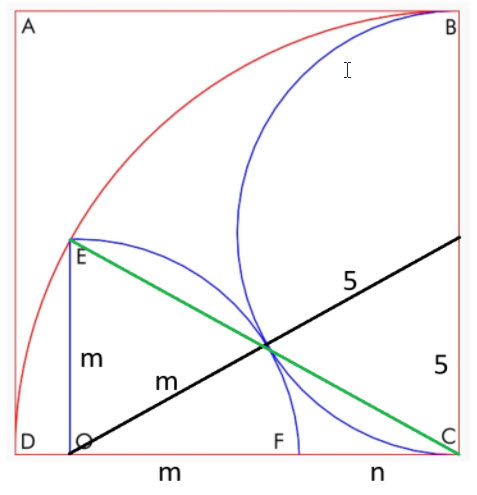
Здесь у нас два прямоугольных треугольника, один с зелёной гипотенузой, а другой с чёрной. Давайте составим два уравнения Пифагора:
- Зелёная гипотенуза: m² + (m+n) ² = 10²
- черная гипотенуза: 5² + (m+n) ² = (m+5) ²
Перегруппируем первое уравнение: (m+n) ² = 10² - m²
Подставим это значение (m+n) ² во второе уравнение:
5² + 10² - m² = (m+5) ²
25 + 100 - m² = m² + 10m + 25
2м² + 10м - 100 = 0
м² + 5м - 50 = 0
Используя формулу Пифагора для вычисления m:
m = (-5 +/- sqrt(25 + 200))/2
m = 5 или -10. 5 — единственный разумный ответ.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Большое количество студентов сдают тест из 10 вопросов. Каждый вопрос либо верен, либо неверен. Каково максимальное количество студентов, которые могут сдавать тест, чтобы любые два теста отличались друг от друга как минимум на два вопроса?
Рассмотрим один тест, который мы назовем ключевым.
Группа 1 = Количество способов, которыми другие тесты могут отличаться ровно на 2 вопроса от ключевого теста, равно combin(10,2)=45.
Я не буду подсчитывать количество способов отличаться на 3 от результатов основного теста, потому что некоторые из этих способов будут совпадать с результатами теста из группы 1 в 9 случаях из 10.
Группа 2 = Количество способов, которыми другие тесты могут отличаться от ключевого теста ровно на 4 вопроса, равно combin(10,4)=210. Любой из этих вариантов также будет отличаться от любого теста в группе 1 как минимум на 2.
Повторим эту логику...
- Группа 3 = Количество способов, которыми другие тесты могут отличаться ровно на 6 вопросов от основного теста, равно combin(10,6)=210.
- Группа 4 = Количество способов, которыми другие тесты могут отличаться ровно на 8 вопросов от основного теста, равно combin(10,8)=45.
- Группа 5 = Количество способов, которыми другие тесты могут отличаться ровно на 10 вопросов от основного теста, равно combin(10,10)=1.
Таким образом, ответ — это сумма групп с 1 по 5 плюс один балл за основной тест = 1 + 45 + 210 + 210 + 45 + 1 = 512.
Это число совпадает с 2^9. Может ли это быть совпадением? Нет!
Количество способов выбрать нечётное число предметов из большой группы равно количеству способов выбрать чётное число. Это потому, что каждый предмет в большой группе может быть либо выбран, либо не выбран. Существует 2^n комбинаций выбора или невыбора каждого элемента в группе из n предметов. Если бы вы перечислили их систематически в двоичном порядке, количество выбранных комбинаций чередовалось бы между чётными и нечётными. Общее число элементов в группе равно 2^n, что само по себе чётно, поэтому половина от 2^n будет чётной.
Таким образом, сумма групп с 1 по 5 равна количеству способов выбрать четное число вопросов, соответствующих ключевому тесту. Это будет равно количеству способов выбрать нечетное число вопросов, соответствующих ключевому тесту. Общее количество способов совпасть или не совпасть с ключевым тестом составляет 2¹⁰ = 1024. Половина из них совпадет четное число раз. Следовательно, ответ 1024/2 = 512.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .


