WOO logo

Wizard рекомендует

Спросите Волшебника #427

Торт делят следующим образом:

  • Первый человек получает 1%.
  • Второй человек получает 2% от оставшейся суммы.
  • Третий человек получает 3% от оставшейся суммы.
  • И так далее.

Кому достанется больше всего торта? Никаких электронных таблиц или расчетов методом перебора.

анонимный

Десятый человек получит больше всего торта.

Вот моё решение (PDF).

Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .

Хочу выразить благодарность YouTube-каналу Mind Your Decisions за эту математическую головоломку.

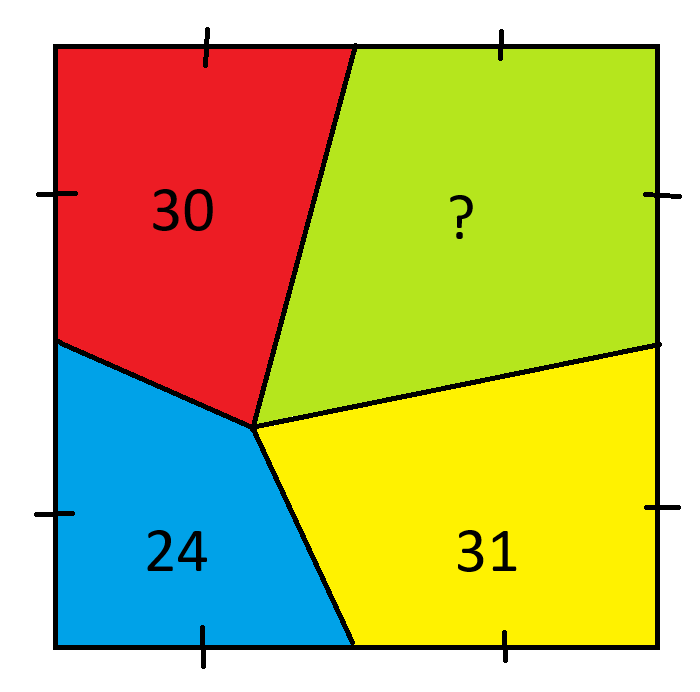
Какова площадь зеленой зоны?

анонимный

38

[spoiler=Решение]

Сначала проведите четыре линии от точки пересечения четырех деталей к каждому углу. Затем обозначьте восемь деталей следующим образом.

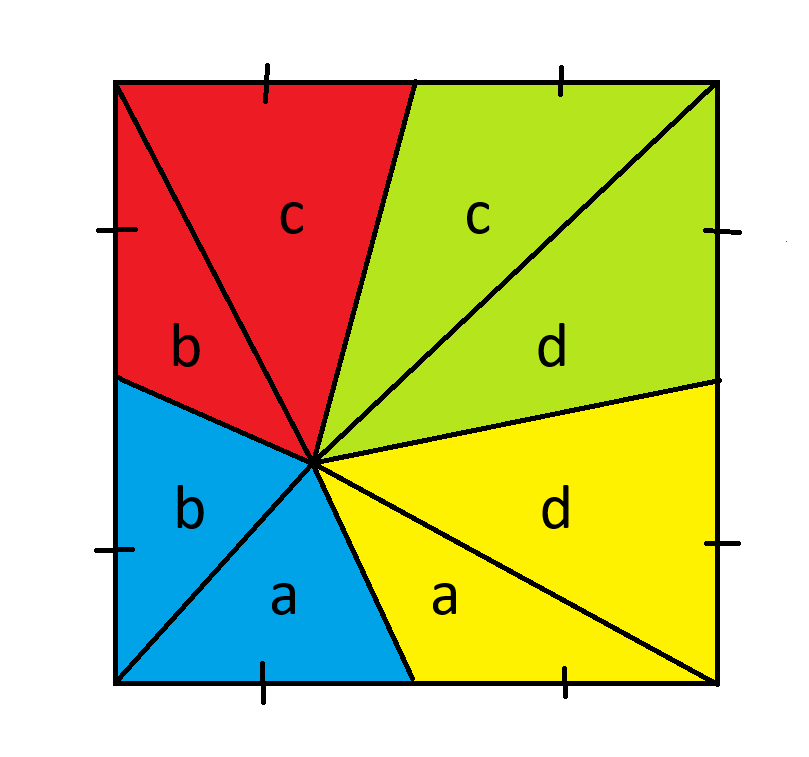
Напомним, что площадь треугольника равна произведению основания на высоту и деления на 2. Поскольку все треугольники имеют одинаковое основание, можно считать, что треугольники одинаковой высоты имеют одинаковую площадь.

На данный момент нам известно:

  • (1) A+B = 34
  • (2) B+C = 42
  • (3) A+D = 30

Складывая уравнения (2) и (3):

A+B+C+D = 72

Вычтем из этого уравнение (1):

C+D = 38, что и является нашим ответом.

[/спойлер]

Этот вопрос был задан и обсуждался на моём форуме, посвящённом игре Wizard of Vegas .

Источник головоломки — видео на YouTube под названием «98% НЕ СПРАВИЛИСЬ с решением этой математической задачи».

Допустим, вы хотите найти среднее значение нескольких величин. Каково ваше мнение о том, чтобы отбрасывать самые высокие и самые низкие значения, как это делают при подсчете баллов в гимнастике на Олимпийских играх? Допустим, цель состоит в том, чтобы найти среднее значение на квадратный фут в определенном районе.

анонимный

Хороший вопрос. То, о чём вы говорите, называется усечённым средним. Мне неизвестна статистика для измерения отклонения усечённого среднего от истинного среднего. За неимением лучшей идеи, я провёл собственный эксперимент.

Чтобы ответить на ваш вопрос, я взял 100 000 выборок из десяти наборов значений. Каждое значение было распределено в соответствии со стандартным нормальным распределением, то есть со средним значением 0 и дисперсией 1. Затем я рассмотрел среднее значение всех десяти значений, а также среднее значение восьми отсеченных значений.

В результате я обнаружил, что средняя разница между выборочным средним и истинным средним значением, полученным при выборке всех десяти значений, составила 0,003450. При выполнении той же операции, но с усреднением усеченного среднего, средняя разница составила 0,003445. На мой взгляд, это недостаточно существенная разница, чтобы утверждать, какой метод лучше. Кроме того, то, что подходит для моего эксперимента, может не подойти для другого применения.

В заключение, хотя я редко это говорю, у меня нет однозначного математического ответа.

Какой способ укладки шаров с квадратным или треугольным основанием является наиболее эффективным (то есть с наименьшим количеством нерационально используемого пространства)?

анонимный

Я ответил на этот вопрос, исходя из того, какая пирамида имеет наибольшее отношение объема сфер к объему пирамиды, вмещающей их, при стремлении числа сфер к бесконечности.

Они одинаково эффективны, их эффективность составляет 74,05%.

Вот моё решение (PDF).

Позже я понял, что этот вопрос также задавался в рубрике «Спроси волшебника» № 350. Однако я считаю, что это решение лучше.