Вероятность - Карты
Я играл в баккару онлайн, и из 75 раздач банкир выиграл 52, а игрок — 23. Разница составляет 29. Какова вероятность такого исхода?
Во-первых, я предположу, что вы не учитываете ничьи. Другими словами, вы имеете в виду 75 завершенных ставок. Маловероятно, что за 75 раздач не будет ни одной ничьи. Ожидаемое количество выигрышей банкира из 75 завершенных ставок составляет 38,00913745. Стандартное отклонение — это квадратный корень из произведения 75, вероятности выигрыша банкира и вероятности выигрыша игрока. Вероятность выигрыша банкира при отсутствии ничьей составляет 0,506788499, а вероятность выигрыша игрока — 0,493211501. Таким образом, стандартное отклонение равно 4,329727904. Затем вам нужно будет внести поправку в полпункта для биномиального распределения и найти Z-статистику в стандартной нормальной таблице (этот шаг оставлен на усмотрение читателя). Окончательный ответ: вероятность того, что банкир получит 52 или более выигрышей, составляет 0,0009. В вашем вопросе также допускалась возможность того, что банкир выиграет 23 или менее раз (также с разницей в 29 и более раз), что имеет вероятность 0,0004. Таким образом, окончательный ответ заключается в том, что вероятность разницы в 29 или более раз составляет 0,0013, или 1 к 769.
Когда я рассчитываю комбинации рук игрока и дилера в Caribbean Stud Poker , я получаю всего 3 986 646 103 440 против ваших 19 и т.д. Моя ошибка ровно в 5 раз. Я использовал combin (52,5)*combin(47,5). Где я допустил ошибку? Спасибо, и я считаю ваш сайт просто замечательным.
Спасибо за комплимент. Вы ошиблись в пять раз, потому что у дилера может быть любая из 5 карт лицевой стороной вверх. Другими словами, порядок имеет значение для руки дилера, поскольку первая карта раздаётся лицевой стороной вверх. Правильный вывод общего количества комбинаций: combin(52,5)*combin(46,4) = 19 933 230 517 200.
Каковы шансы вытянуть три карты в пару и получить фулл-хаус в пятикарточном покере?
В этой ситуации есть два способа собрать фулл-хаус: (1) вытянуть три одинаковые карты или (2) вытянуть еще одну карту к паре и еще одну пару. Я предполагаю, что вы сбросите три одиночные карты.
Сначала вычислим количество комбинаций в соответствии с (1). Есть 3 ранга, в которых осталось только 3 масти (помните, вы сбросили 3 одиночные карты), и 9 рангов, в которых осталось 4 масти. Таким образом, количество комбинаций равно 3*комбинация(3,3) + 9*комбинация(4,3) = 3*1 + 9*4 = 39.
Далее, давайте вычислим количество комбинаций по (2). Осталось добавить 2 масти к существующей паре. Существует (3,2) способов составить пару из 3 рангов, имея 3 оставшиеся карты, и (4,2) способов составить пару из рангов, имея 4 оставшиеся карты. Таким образом, общее количество комбинаций по (2) равно 2*(3*комбинация(3,2)+9*комбинация(4,2)) = 2*(3*3 + 9*6) = 126. Общее количество способов составить фулл-хаус равно сумме по (1) и (2), или 39+126=165. Существует (47,3)=16215 способов составить 3 карты при втором вытягивании. Вероятность выпадения фулл-хауса равна числу способов выпадения фулл-хауса, деленному на общее количество комбинаций, или 165/16215 = 0,0101758, или примерно 1 к 98.
Для получения более подробной информации о функции combin() см. раздел о вероятностях в покере на моей странице.
Я начал играть в покер с друзьями раз в неделю (пятикарточный дро, стад, семикарточный стад). За столом семь игроков. Мне кажется, вероятность получить нужные комбинации значительно снизится из-за того, что игрокам будут выдаваться карты из колоды в 52 карты. Есть ли у вас математическая формула, которая могла бы подсказать мне правильное направление?
Нет, вероятность получить любую конкретную комбинацию карт одинакова независимо от количества других игроков за столом. Невидимая карта остаётся невидимой, неважно, есть ли она у другого игрока или всё ещё находится в колоде.
Недавно мне рассказали историю, в которую я не мог поверить! Мой друг рассказал, что во время дружеской игры в покер у него дома они с другом собрали натуральный стрит-флеш в одной раздаче, не взяв ни одной карты в дро-режиме! (при пятикарточном дро-режиме) Мне трудно в это поверить, и, используя ваш сайт, я подсчитал, что вероятность выпадения одного стрит-флеша составляет примерно 65 000 к одному. Какова будет вероятность выпадения двух стрит-флешей в одной раздаче при шести игроках (без дро-карт)?
Я дам приблизительный ответ, предполагая, что каждому игроку раздали карты из разных колод. Это не должно сильно изменить шансы. Вероятность того, что любой игрок соберет стрит-флеш, как показано в моем разделе о вероятностях в покере, составляет 36/2 598 960. Назовем эту вероятность p. Вероятность того, что два игрока соберут стрит-флеш, равна (6,2)* p² *(1-p) ⁴ = 0,0000000028779. Другими словами, шансы на то, что это произойдет, составляют 347 477 740 к 1.
Как рассчитать отдельные вероятности получения: (1) дамы старшей карты, (2) короля старшей карты и (3) туза старшей карты в покере с тремя картами?
Сначала я вычислю вероятность для комбинации с королём, а для двух других кратко покажу формулу. Вероятность будет равна количеству комбинаций с королём, делённому на общее количество комбинаций. Количество рангов меньше короля равно 11. Комбинация с королём должна содержать два разных ранга. Количество способов составить 2 из 11 комбинаций равно (11,2) = 55. Однако одна из этих комбинаций — король-дама-валет, что приводит к стриту, поэтому, вычитая эту комбинацию, остаётся 54 комбинации, которые не образуют стрит. Далее, для каждого ранга существует четыре масти, или 4³ = 64 возможных комбинации мастей. Однако четыре из этих 64 комбинаций приводят к флешу, поэтому остаётся 64-4 = 60 комбинаций мастей. Таким образом, общее количество комбинаций с королём равно 54*60 = 3240. Всего существует комбинаций (52,3) = 22 100, чтобы составить 3 карты из 52. Таким образом, вероятность составления старшей карты короля составляет 3240/22100 = 0,1466063. Вероятность составления старшей карты туза равна: (комбинация (12,2) - 2) * (4 3 - 4) / комбинация (52,3) = 0,1737557. Обратите внимание на -2 вместо -1, потому что есть стриты a-2-3 и qka.
Вероятность выпадения старшей королевы равна: (комбинация(10,2)-1)*(4 3 -4)/комбинация(52,3)=0,119457.
Каковы шансы получить роял-флеш? Шансы получить последовательный роял-флеш (вперед или назад)?
Вероятность выпадения любого роял-флеша равна числу возможных роял-флешей, которое равно четырем (по одной для каждой масти), деленному на число способов выбрать 5 карт из 52, что равно комбинации (52,5) = 2 598 960. Таким образом, ответ равен 4/2 598 960 = 0,00000153908, или 1 из 649 740.
Вероятность последовательного роял-флеша равна (количество мастей) * (количество направлений) / (общее количество перестановок 5 карт из 52) = 4 * 2 / перестановка (52,5) = 8 / 311 875 200 = 8 / количество возможных роял-флешей, которое равно четырем (по одному для каждой масти), умноженное на количество направлений, в которых он может находиться, и деленное на количество способов выбрать 5 карт из 52, которое равно перестановке (52,5) = 311 875 200. Таким образом, ответ равен 4/311 875 200 = 0,00000002565, или 1 из 38 984 400.
Мне нравится играть в покер «Лжецы» с долларовыми купюрами. Какова вероятность того, что на купюре выпадет любая цифра 1, 2, 3, 4 или 5? Спасибо. Если я играю втроем, какова вероятность того, что выпадет хотя бы одна цифра?
Сначала позвольте мне ответить на незаданный вопрос о вероятности того, что определённое число появится n раз на случайной купюре. На купюре 8 цифр, поэтому вероятность появления n определённого числа равна combin(8,n)*0.1 n *0.9 8-n /10 8 . Вот таблица, показывающая вероятность появления от 0 до 8 определённого числа.
Нечетность конкретных чисел в покере лжецов
| Число | Вероятность |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| Общий | 1.00000000 |
В следующей таблице показана вероятность каждого возможного типа купюр, сгруппированных по количеству каждого вида n одинаковых купюр. Например, для серийного номера 66847680 будет одна тройка одинаковых купюр, одна пара и три одиночные купюры, что соответствует вероятности 0,1693440.
Общие вероятности в игре "Покер лжецов"
| 8 дубов | 7 дубов | 6 дубов | 5 дубов | 4 дуба | 3 дуба | 2 дуба | 1 дуб | Вероятность |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| Общий | 1.0000000 | |||||||
дуб = "своего рода"
Для получения более подробной информации посетите мою страницу о покере лжецов .
Какова вероятность вытянуть пару валетов из колоды из 52 карт?
Предположим, вы вытягиваете пять карт и считаете все руки, в которых ровно два валета. Тогда вероятность составит combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3,99%.
Какова вероятность получить три пары в Пай Гоу Покере? Вероятность меньше или больше, чем при выпадении трёх одинаковых карт?
Не считая трех одинаковых карт и двух пар, ниже приведены способы получения трех пар и количество комбинаций.
Без подстановочного знака: combin(13,3)*10*6 3 *4 =2471040
Вишенка, используемая для сравнения пары тузов: combin(12,2)*10*6 2 *4 2 = 380,160
В качестве единственного туза используется подстановочная карта: combin(12,3)*6 3 = 47,520
Общее количество комбинаций составляет 2 898 720. Это менее половины от 747 0676 комбинаций для тройки одинаковых карт.
Согласно вашей формуле, вероятность выпадения роял-флеша составляет 4/2 598 960 = 1/649 740. Таким образом, если бы я играл в карибский стад один на один с дилером, то моя рука и рука дилера составили бы 649 740 * 2 = 1 299 480. Следовательно, согласно расчетам, после 1 299 480 раздач должно быть два роял-флеша. Пожалуйста, объясните, правильно ли я понимаю вероятность.
Вы правы, в среднем роял-флеш выпадает один раз на каждые 649 740 раздач, а в 1 299 480 раздачах ожидаемое количество роял-флешей составляет 2. Однако это только среднее значение. С каждой последующей раздачей вы не приближаетесь к получению роял-флеша. В любой игре на выбывание есть это свойство отсутствия памяти, поэтому роял-флеш никогда не бывает запоздалым.
Вероятность выпадения нуля роял-карт в 1 299 480 раздачах составляет 13,53%.
Привет! Я постоянный игрок в Пай Гоу Покер, и заметил, что на вашем сайте много полезной информации об этой игре. На днях, когда я играл с другом, ему досталась комбинация из девятки, которая, как я полагаю, является самой младшей возможной комбинацией. За всё время, что я играю, такое случалось всего один раз. Затем, через пять раздач, ему досталась точно такая же комбинация (2-3-4-5-7-8-9). Мы не могли поверить своим глазам и задумались о вероятности такого исхода, поэтому решили спросить у вас. Спасибо за ваше время и за ваш замечательный сайт.
Существует два способа упорядочить карты для формирования комбинации из девятки: тот, который вы упомянули, и 2-3-4-6-7-8-9. Количество комбинаций мастей без формирования флеша составляет 4 7 -4*(комбинация(7,5)*3^2+6*3+1) = 15 552. Таким образом, вероятность получения комбинации из девятки равна 2*15 552/комбинация(53,7) = 31 104/154 143 080, или 1 к 9911. Если бы вы сыграли всего пять раз, вероятность получить две комбинации из девятки составила бы 1 к 9 826 685. Я считаю, что это совпадение, а не ошибка в генераторе случайных чисел или в коде программы.
Мой вопрос касается расчета преимущества казино и элемента риска в игре Casino War по правилам Casino Niagara (то есть, выплата 3 к 1 при повышении ставки и проигрыш первоначальной ставки). Как вы получили эти цифры? Я сейчас пытаюсь их рассчитать, но у меня возникают трудности. Спасибо за помощь.
Пусть d — количество колод. Вероятность ничьей в первом раунде равна (4*d-1)/(52*d-1) = 0,073955. Вероятность ничьей во втором раунде равна 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0,073974. Назовем p1 вероятностью ничьей в первом раунде, а p2 — вероятностью ничьей во втором раунде. Тогда выигрыш игрока равен p1 *(2* p2 +(1- p2 )/2*(1-2)) = -0,023301. Умножим на -1, и получим преимущество казино в 2,33%. Надеюсь, я не слишком быстро объяснил это.
Не могли бы вы объяснить, как получилось общее количество комбинаций в Карибском бассейне, равное 19 933 230 517 200? Я использовал ваши комбинации для 5-карточного покера, чтобы получить 2 598 960. Как мне действовать дальше? Заранее спасибо.
Вы правильно рассчитали количество комбинаций игроков: combin (52,5)=2 598 960. Таким образом, у дилера может быть combin(47,5)=1 533 939 возможных комбинаций. При этом любая из пяти карт дилера может быть открыта. Следовательно, 2 598 960*1 533 959*5=19 933 230 517 200.
Прежде всего, хочу сказать, что ваш сайт действительно замечательный. Я рассказал о нём нескольким людям и надеюсь, что они тоже его попробуют. Желаю вам дальнейших успехов. Мне также понравилась ссылка на WinPoker. WinPoker мне настолько понравился, что я его заказал. Это отличная программа. У меня есть вопрос, с которым, я надеюсь, вы сможете мне помочь. Я пытаюсь выяснить, сколько раз встречается каждая раздача в семикарточном стаде. У меня есть копия вашей таблицы для семикарточных раздач, но меня интересует математическая формула, необходимая для получения этих чисел. Я могу вычислить количество раздач для пятикарточных раздач, но семикарточные меня просто сбивают с толку. Я хотел бы отправить файл Excel 2000 со своими данными. Я также хотел бы узнать, как вычислить количество стрейтов в колоде из 53 карт с джокером. ПОМОГИТЕ!!!
Спасибо за добрые слова. Я согласен, что подсчет чисел в семикарточном стаде — сложная задача. Поэтому я делаю это на компьютере. Моя программа перебирает все возможные комбинации и оценивает каждую из них. Количество джокеров в пай-гоу-покере составляет 11*(4 4 -4)+10*3*(4 4 -4)=10332. В сочетании с 10200 натуральными стритами общая сумма составляет 20532.
Я понимаю, каковы шансы получить роял-флеш или стрит-флеш для любого игрока за столом в Caribbean Stud Poker или Let it Ride и как они рассчитываются. Но мой вопрос вот в чём: каковы шансы увидеть любую из этих рук, сданную игроку за столом в любой конкретной раздаче? Я полагаю, это зависит от количества раздач... это просто шансы отдельного игрока, умноженные на количество раздач? То есть, если увидеть роял-флеш в любой конкретной раздаче при наличии 4 игроков за столом, значит, шансы получить роял-флеш равны 4 * ? Я немного озадачен!
Ваш метод является хорошим приближением. Однако, следуя этой логике, при подбрасывании монеты вероятность того, что хотя бы один человек из 3 выпадет орлом, составит 3*50%=150%. Предполагая независимость событий, вероятность хотя бы одного успеха из n испытаний, где вероятность каждого успеха равна p, равна 1-(1-p) n . В случае примера с подбрасыванием монеты это будет 1-0,5/ 3 = 0,875. В случае четырех игроков в карибский стад-покер вероятность хотя бы одного роял-флеша составит 1-(1-4/2598960) 4 = 0,00000615629. Однако, поскольку все карты раздаются из одной колоды, события не являются независимыми. Математические вычисления становятся очень сложными для определения точного ответа, и приближение должно быть очень близко к правильному ответу.
Какова вероятность получить натуральный стрит-флеш из семи карт в пай-гоу покере? Я работаю в казино и только что впервые за 15 лет увидел это. Счастливчик выиграл 40 000 долларов.
Существует 32 возможных естественных стрит-флеша (4 ранга умножить на 8 возможных комбинаций из 7 карт). Комбинаций (53,7) = 154143080 существует возможных способов вытянуть 7 карт из 53. Таким образом, ответ равен 32/154143080, или 1 из 4816971.
Какова вероятность получить два одинаковых стрит-флеша (по рангу и масти) две раздачи подряд в трехкарточном покере?
Вероятность получить стрит-флеш в первой раздаче составляет 4*12/комбинация(52,3) = 48/22100 ≈ 0,0022. Вероятность того, что следующая раздача будет точно такой же, составляет 1/22100. Таким образом, ответ (48/22100)*(1/22100) = 48/488410000, что составляет 1 к 10 175 208. Это в 1,37 раза вероятнее, чем выигрыш в лотерее 6/49, вероятность которого составляет 1 к 13983816.
В баккара с 8 колодами, какова вероятность того, что игрок и банкир получат туз и восьмерку бубен в одной и той же раздаче?
(8 2 /combin(416,2))* (7 2 /combin(414,2)) = 0,00000043 или 1 из 2308093
Недавно я стал свидетелем странного события. Я смотрел покер с пятью картами, где можно было взять максимум две карты. Один игрок взял одну карту и собрал флеш червей. Дилер взял одну карту и собрал флеш пик. Естественно, флеш дилера был выше. В игре участвовали ещё три игрока. Какова вероятность того, что в одной раздаче окажутся два флеша?
Давайте определим вероятность флеша: либо получить его при раздаче, либо собрать флеш из 4 карт. Для простоты предположим, что игрок соберет пару или стрит с 4 картами для флеша. Вероятность получить флеш при раздаче (не включая стрит/роял-флеш) составляет 4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0,0019654. Вероятность получить флеш из 4 карт составляет 4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0,0429172. Вероятность собрать флеш при дро составляет 9/47. Таким образом, общая вероятность получить флеш из 4 карт и затем завершить его составляет 0,0429172*(9/47) = 0,0082182. Следовательно, общая вероятность флеша равна 0,0019654 + 0,0082182 = 0,0101836. Вероятность того, что ровно 2 из 5 игроков получат флеш, составляет combin(5,2)* 0,0101836 2 *(1-00,0101836) 3 = 0,001006, или примерно 1 к 994.
Мне нужно узнать вероятность того, что кто-то соберет четыре одинаковые карты за раздачу в семикарточном стаде с пятью игроками и одной колодой карт? Надеюсь, вы сможете мне помочь, и спасибо за ваше время.
Существует 133 784 560 способов составить комбинацию из 52 карт, включая четыре одинаковые карты. Количество комбинаций из 7 карт, включающих четыре одинаковые карты, равно 13 * комбинаций (48, 3) = 224 848. 13 — это количество рангов для четырех одинаковых карт, а комбинации (48, 3) — это количество способов выбрать три карты из оставшихся 48. Таким образом, вероятность составляет 224 848 / 133 784 560 = 0,0017, или 1 из 595.
Когда вы открываете новую колоду карт, в ней находятся карты от туза до короля каждой масти. Какова вероятность того, что перетасованная колода карт вернется в исходное состояние с тузами и королями?
1 к 52 факториалу, или 1 к 80 658 175 170 943 900 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
Если десяти игрокам раздают по две карты из одной колоды, какова вероятность того, что двум игрокам достанется пара тузов?
Во-первых, существует 10*9/2=45 способов выбрать 2 игроков из 10. Вероятность того, что у двух конкретных игроков окажется четыре туза, равна 1/комбинация(52,4)=1/270725. Таким образом, вероятность того, что у любых двух игроков окажется пара тузов, равна 45/270725=0,0001662.
Если у семи игроков по семь карт, какова вероятность того, что хотя бы у одного из них окажется флеш из семи карт?
Вероятность того, что один игрок соберет флеш из 7 карт, составляет 4*combin(13,7)/combin(52,7) = 1 к 19491. Вероятность того, что хотя бы один игрок из 7 соберет флеш из 7 карт, составляет примерно 1 к 2785.
Я понимаю, что математически возможно всё, но на днях в казино я, кажется, стал свидетелем события, вероятность которого составляет миллиард к одному, хотя такие случаи, конечно, случаются. Вот что произошло: за 40 раздач (40 раздач по 3 карты, около 8 раундов с 5 игроками) за столом Let It Ride было роздано три каре. Учитывая, что вероятность выпадения трёх каре примерно 4100 к одному, какова вероятность того, что три таких карты выпадут за 40 раздач? Пожалуйста, ответьте, потому что это меня просто убивает. Давний поклонник.
Для простоты предположим, что каждая раздача происходит из новой колоды. Вероятность выпадения четырех одинаковых карт составляет 13*48/комбинация(52,5) = 624/2598960. Вероятность выпадения ровно 3 из 40 четырех одинаковых карт составляет комбинация(40,3)*p 3 *(1-p) 37 = 1 из 7378135, где p = 624/2598960. Таким образом, это скорее шанс 1 из 7 миллионов.
Прежде всего, я хотел бы сказать, как сильно мне нравится ваш сайт и как я им восхищаюсь, а также ваши математические способности. Я использую 6 колод для раздачи карт в блэкджеке и добавил 3 джокера по причинам, которыми я не буду вас утомлять, но какова вероятность того, что игроку подряд выпадут все 3 джокера? Большое спасибо.
Пожалуйста, спасибо за комплименты. Вероятность получить 3 джокера подряд из колоды из шести карт (плюс 3 джокера) составляет 1/комбинация(315,3) = 1 из 5 159 805. Другое решение: (3/315)*(2/314)*(1/313).
Какова вероятность того, что каждый из четырех игроков, используя колоду из 52 карт, получит по 13 карт, и у всех четырех игроков окажется стрит от туза до двойки? Карты не обязательно должны быть одной масти.
Ответ: (4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 1 из 61 204 166 001.
Какова вероятность того, что вам выпадет четыре карты против роя?
Для рояльного масти возможны четыре масти. Возможны пять недостающих карт. Пятая карта может быть одной из 47 других карт. Таким образом, существует 4*5*47=940 способов получить четыре карты для рояльного масти. Всего существует комбинаций (52,5) = 2 598 960. Следовательно, вероятность составляет 940/2 598 960 = 1 из 2765.
Уважаемый волшебник, допустим, колода из 52 карт перетасована, и мы случайным образом вытягиваем 18 из 52 карт, распределяя их по 6 стопкам по 3 карты в каждой. Какова вероятность того, что в одной из стопок окажется ровно 3 (из 4) туза?
Проще всего решить эту задачу, так как вероятность того, что в первой стопке окажется три туза, равна (4/52)*(3/51)*(2/50) = 1/5525. Однако вероятность того, что в каждой стопке окажется три туза, одинакова, поэтому мы умножаем на 6, получая 6/5525 = 0,001086
Какова вероятность получить все карты с картинками в пятикарточном стаде?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0,00030474, или примерно 1 к 3282.
Какова вероятность получить две одинаковые карты (четыре одинаковые) за два часа игры в Let it Ride?
Вероятность выпадения четырех одинаковых карт в любой раздаче составляет 13*48/combin(52,5) = 0,0002401. Предположим, что за два часа вы можете сыграть 120 раздач. Вероятность выпадения ровно двух четырех одинаковых карт составит combin(120,2) × 0,0002401 2 × (1-0,0002401) 118 = 0,000400095 = 1 из 2499,41.
В покере с четырьмя картами, что более вероятно для стрита или флеша?
Если не учитывать стрит-флеши и роял-флеши, вероятность стрита составляет 1,02%, а флеша — 1,04%. Таким образом, вероятность флеша немного выше.
Какова вероятность того, что за 1 миллион раздач наступит засуха роял-флешей, которая продлится 200 000 раздач? Меня больше интересует решение, чем сам ответ.
Я нечасто это говорю, но я пытался решить эту задачу несколько часов, однако математические вычисления оказались мне совершенно непонятны. Поэтому я обратился к своему другу и профессору математики Габору Мегеши. Вот его формула для любой задачи, связанной с засухой.
- Пусть p — вероятность выигрыша в любой данной раздаче.
- Пусть d — продолжительность засухи.
- Пусть n — количество сыгранных раздач.
- Пусть k=dp и x=np.
- Если k=1, то пусть a=-1, в противном случае найдите a такое, что k=-ln(-a)/(1+a). (a — отрицательное число; если k>1, то -1 < a < 0, если k < 1, то a < -1, и a необходимо вычислить с высокой точностью.) [Примечание мастера: подобное решение легко найти в Excel с помощью функции «Поиск решения» в меню «Инструменты».]
- Если k=1, то пусть A=2, в противном случае пусть A=(1+a)/(1+ak).
- Вероятность отсутствия засухи продолжительностью d в n руках составляет приблизительно Ae a x .
В данной конкретной задаче p=1/40391, d=200000, n=1000000, k=4.9516, x=24.758, a=-0.0073337, A=1.03007. Таким образом, вероятность отсутствия засухи составляет 1.03007*e -0.0073337*24.758 = 0.859042. Следовательно, вероятность хотя бы одной засухи равна 1-0.859042 = 0.140958.
Вот полное 5-страничное решение Габора Мегеши (PDF). Спасибо Габору за помощь.
Я провел случайное моделирование 32 095 наборов по миллиону раздач. Число раздач, в которых хотя бы один раз не было ни одной, составило 4558, что соответствует вероятности 14,20%.
Предположим, у вас есть две пятикарточные покерные комбинации из разных колод. Вам сказано, что в комбинации А есть как минимум один туз. Вам сказано, что в комбинации В есть туз пик. В какой комбинации с большей вероятностью будет хотя бы на один туз больше?
В следующей таблице показана вероятность выпадения от 0 до 4 тузов в совершенно случайной раздаче.
Вероятности выпадения туза — случайная рука
| Тузы | Формула | Комбинации | Вероятность |
|---|---|---|---|
| 0 | комбин(48,5) | 1712304 | 0.658842 |
| 1 | combin(4,1)×combin(48,4) | 778320 | 0.299474 |
| 2 | combin(4,2)×combin(48,3) | 103776 | 0.03993 |
| 3 | combin(4,3)×combin(48,2) | 4512 | 0.001736 |
| 4 | combin(4,4)×combin(48,1) | 48 | 0.000018 |
| Общий | 2598960 | 1 |
Рассмотрим сумму вероятностей выпадения от 1 до 4 тузов: вероятность выпадения хотя бы одного туза составляет 0,341158. Вероятность выпадения двух или более тузов равна 0,041684.
Вероятность наличия хотя бы одного дополнительного туза при условии наличия хотя бы одного, может быть переформулирована согласно теореме Байеса как вероятность (два дополнительных туза при условии наличия хотя бы одного туза) = вероятность (два или более туза) / вероятность (наличие хотя бы одного туза) = 0,041684 / 0,341158 = 0,122185.
Для тех, кто подзабыл теорему Байеса, она гласит, что вероятность события А при условии события В равна вероятности событий А и В, деленной на вероятность события В, или Pr(A при условии события В) = Pr(A и B)/Pr(B).
В следующей таблице показаны комбинации и вероятность выпадения каждого числа других тузов при условии, что туз пик был удален из колоды.
Вероятность выпадения туза — рука без туза
| Тузы | Формула | Комбинации | Вероятность |
|---|---|---|---|
| 0 | combin(3,0)×combin(48,4) | 194580 | 0.778631 |
| 1 | combin(3,1)×combin(48,3) | 51888 | 0.207635 |
| 2 | combin(3,2)×combin(48,2) | 3384 | 0.013541 |
| 3 | combin(3,3)×combin(48,1) | 48 | 0.000192 |
| Общий | 249900 | 1 |
Это показывает, что вероятность появления хотя бы еще одного туза составляет 0,221369.
Для интереса решим ту же задачу, используя теорему Байеса. Предположим, что случайные руки раздаются до тех пор, пока не окажется одна, содержащая туз пик. Вероятность наличия хотя бы одного дополнительного туза при условии, что рука содержит туз пик, можно переписать как вероятность (по крайней мере два туза при условии, что в руке есть туз пик). Согласно теореме Байеса, это равно Вероятность (рука содержит туз пик и хотя бы один дополнительный туз) / Pr(рука содержит туз пик). Мы можем разложить числитель как Вероятность (2 туза, включая туз пик) + Вероятность (3 туза, включая туз пик) + Вероятность (4 туза). Используя первую таблицу, это равно 0,039930 × (2/4) + 0,001736 × (3/4) + 0,000018 = 0,021285. Вероятность выпадения туза пик составляет 5/52 = 0,096154. Следовательно, вероятность выпадения как минимум двух тузов при наличии тузов пик равна 0,021285/0,096154 = 0,221369.
Таким образом, вероятность выпадения двух или более тузов при наличии хотя бы одного туза составляет 12,22%, а при наличии туза пик — 22,14%.
Хорошо, я верю вашим расчетам, но мне это все равно не кажется логичным. Вероятности должны быть равны. Какая разница, какая масть у того единственного туза, который вам выпал?
Рассмотрим другую, более простую ситуацию. Предположим, женщина А говорит: «У меня двое детей, и как минимум один из них — мальчик». Женщина Б говорит: «У меня двое детей, и старшего зовут Джон». Мы можем предположить, что ни у кого нет девочки по имени Джон, и ни одна женщина не дает одно и то же имя более чем одному ребенку. Используя условную вероятность, вероятность того, что оба ребенка женщины А будут мальчиками, равна pr(оба мальчика)/pr(как минимум один мальчик) = pr(оба мальчика)/(1-pr(оба девочки)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3. Однако вероятность того, что младший ребенок женщины Б — мальчик, или что оба ребенка — мальчики, равна ?, потому что утверждение, что старшего ребенка зовут Джон, ничего не говорит нам о младшем ребенке.
В качестве другого примера предположим, что вы зашли в Jiffy Lube, и вам предложили два варианта по одной и той же цене. Вариант А: они проверят четыре детали и заменят только первую обнаруженную неисправную. Вариант Б: они проверят только одну проблему и устранят её, если она будет обнаружена. Разве вы не предпочли бы вариант А? Ваша машина приехала с тем же количеством ожидаемых неисправных деталей, но вероятность обнаружения проблемы выше по варианту А, и, следовательно, вы уедете с небольшим количеством ожидаемых неисправных деталей. Аналогично, проверка на любой туз, вероятно, выявит единственный туз, в то время как проверка на туз пик не проверяет остальные три масти, что делает их более вероятными тузами.
Как вы получили число стрит-флешей, собранных из 4 карт из 5 в игре Four Card Poker, равное 2072?
Сначала я разделил стрит-флеши на два типа: с четырьмя последовательными одномастными картами и с пятью. Количество стрит-флешей из пяти карт равно количеству мастей * количеству комбинаций (от туза до десятки как младшая карта) = 4*10 = 40. Для стрит-флешей из четырех карт существует 11 различных комбинаций (от туза до валета как младшая карта). В случае стрит-флешей A234 и JQKA пятая карта может быть одной из 47 (52 минус 4 уже удаленные карты и пятая карта, которая образовала бы стрит-флеш из 5 карт, которые уже были учтены). Таким образом, существует 4*2*47=376 стрит-флешей из комбинаций A234 или JQKA. Из остальных девяти существует 46 возможных карт для пятой карты (52 минус 4 уже удаленные карты и две карты, которые образовали бы стрит-флеш из пяти карт). Таким образом, количество стрит-флешей из комбинаций 2345 до TJQK составляет 4*9*46=1656. Таким образом, общее количество стрит-флешей из 4 карт составляет 40 + 376 + 1656 = 2072.
Флеш на 17-й карте возможен на 100% независимо от обстоятельств. Когда и на какой карте возможен стрит-флеш?
Стрит гарантирован только при наличии 45 карт. Например, вы можете раздать все тузы, двойки, тройки, четверки, шестерки, семерки, восьмерки, девятки, валеты, дамы и короли (всего 44 карты) и все равно не собрать стрит.
Уважаемый, великий волшебник вероятностей! Я в полном восторге от вашей статистической проницательности. Не могли бы вы, пожалуйста, рассчитать для меня вероятность выпадения семикарточного стрита — то есть A, 2, 3, 4, 5, 6, 7 или 2, 3, 4, 5, 6, 7, 8 или 7, 8, 9, 10, валет, дама, король — в семикарточном стаде? Мы понимаем, что это не настоящая покерная комбинация, однако она возникла во время нашей игры, и нам стало интересно, имеет ли она меньшую вероятность, чем обычный фулл-хаус в семикарточном стаде. Спасибо, о знающий человек!
Как я могу отказать после того, как ты так искусно меня польстил? Во-первых, существует комбинаций (52,7) = 133 784 560 способов выбрать 7 карт из 52, не обращая внимания на порядок. Существует 8 возможных комбинаций для стрита из 7 карт (самая младшая карта может быть от туза до восьмерки). Если бы у нас было 7 разных рангов, то существует 4 7 = 16384 способа расположить масти. Обратите внимание, что это включает все карты одной масти, которые образуют стрит-флеш. Таким образом, вероятность составляет 8*16384/133 784 560 = 1 из 1020,6952.
Если из одной колоды я раздам 4 карты, какова вероятность того, что хотя бы одна карта будет пиковой масти?
Вероятность выпадения нуля пик равна (39/52)*(38/51)*(37/50)*(36/49) = 0,303818. Следовательно, вероятность выпадения хотя бы одной пики равна 1-0,303818 = 0,696182.
В игре с одной колодой, какова вероятность получить хотя бы один туз и одну двойку из четырех карт? Это полезно знать для игры в Омаху.
Из теории вероятности 101 мы знаем, что Pr(A или B) = Pr(A) + Pr(B) - Pr(A и B). Следовательно, Pr(A и B) = Pr(A) + Pr(B) - Pr(A или B). Пусть A получит туз, а B — двойку. Pr(A) = Pr(хотя бы один туз) = 1 - Pr(нет тузов) = 1 - комбинация (48,4) / комбинация (52,4) = 1 - 0,7187 = 0,2813. Вероятность отсутствия двойок, очевидно, будет такой же. По той же логике, pr(A или B) = Pr(хотя бы один туз или двойка) = 1 - Pr(нет ни тузов, ни двойок) = 1 - комбинация (44,4) / комбинация (52,4) = 1 - 0,501435 = 0,498565. Таким образом, вероятность получить хотя бы один туз и одну двойку составляет 0,2813 + 0,2813 - 0,498565 = 0,063962.
Какова вероятность получить валета бубен 27 раз подряд в игре с шестью картами?
Вероятность получить это в любой раздаче составляет 6/52. Вероятность получить это в 27 раздачах подряд составляет (6/52) ²⁷ = 1 к 20 989 713 842 161 800 000 000 000.
Какова вероятность получить «руку мертвеца», то есть две пары тузов и восьмерок?
Существует шесть способов расположить две масти из четырех для каждой пары. Затем есть 44 карты для одиночной комбинации. Таким образом, количество успешных комбинаций составляет 6*6*44 = 1584. Всего существует 2 598 960 комбинаций, поэтому вероятность составляет 0,0609%.
Я понимаю, вы уже ответили, что вероятность получить «руку мертвеца» — пару тузов и восьмерок — составляет 0,0609% 3 апреля 2005 года , но я считаю, что «рука мертвеца» — это «два черных туза, две черные восьмерки и дама треф». Какова вероятность вытянуть именно эту комбинацию из одной стандартной колоды?
Получить именно такую комбинацию карт можно только одним способом. Таким образом, вероятность составит 1 в комбинации (52,5) или 1 из 2 598 960.
Каковы шансы/вероятность каждой возможной пятикарточной комбинации из стандартной колоды в 52 карты, где масть одной неповторяющейся карты в комбинации считается общей? Например, рассмотрим комбинацию A♠ A♣ A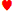 А
А 2. В этой раздаче масть двойки игнорируется и может представлять любую из четырех двоек в колоде. Другой пример: AJ-8-6-5. В этой раздаче масть всех пяти карт игнорируется, так что может возникнуть только одна такая комбинация. Еще один пример: 3♠ 3
2. В этой раздаче масть двойки игнорируется и может представлять любую из четырех двоек в колоде. Другой пример: AJ-8-6-5. В этой раздаче масть всех пяти карт игнорируется, так что может возникнуть только одна такая комбинация. Еще один пример: 3♠ 3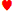 7♣ 7♠ Q. В этой раздаче масть двух троек и двух четверок не игнорируется, потому что их в руке больше одной, но масть дамы является общей. Другими словами, масть любой карты, которая не повторяется в руке, игнорируется, и эта рука считается одной из возможных, даже несмотря на то, что было бы много возможностей повторить эту руку, если бы масть каждой карты не игнорировалась. Таким образом, стрит или флеш, состоящий из пяти конкретных карт, скажем, дамы.
7♣ 7♠ Q. В этой раздаче масть двух троек и двух четверок не игнорируется, потому что их в руке больше одной, но масть дамы является общей. Другими словами, масть любой карты, которая не повторяется в руке, игнорируется, и эта рука считается одной из возможных, даже несмотря на то, что было бы много возможностей повторить эту руку, если бы масть каждой карты не игнорировалась. Таким образом, стрит или флеш, состоящий из пяти конкретных карт, скажем, дамы.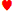 J♣ 10
J♣ 10 9
9 Комбинация 8♠ или A♠ J♠ 8♠ 7♠ 3♠ может встречаться только один раз, поскольку любая другая комбинация этих же карт, даже если они другой масти, будет дублированием. Следовательно, используя этот критерий, каков выходной результат любой раздаваемой руки? Другими словами, сколько таких пятикарточных комбинаций существует в стандартной колоде из 52 карт? Спасибо за ваши ответы.
Комбинация 8♠ или A♠ J♠ 8♠ 7♠ 3♠ может встречаться только один раз, поскольку любая другая комбинация этих же карт, даже если они другой масти, будет дублированием. Следовательно, используя этот критерий, каков выходной результат любой раздаваемой руки? Другими словами, сколько таких пятикарточных комбинаций существует в стандартной колоде из 52 карт? Спасибо за ваши ответы.
Мне эта концепция хорошо знакома. Существует 134 459 уникальных пятикарточных комбинаций. Я знаю это, потому что моя первая программа для видеопокера проанализировала все 2 598 960 возможных комбинаций и потратила несколько дней на обработку таблицы выплат. Однако, обработав всего один пример из каждого из 134 459 классов комбинаций, взвесив их по количеству всех комбинаций в этом классе, можно сократить время выполнения на 95%. Иногда, когда игра имеет специфическую масть, как, например, мой недавний анализ Black Jack Bonus Poker , мне приходится доставать свою старую программу и делать это медленным способом.
Каковы вероятности в пятикарточном стаде, если использовать колоду с 5 мастями вместо 4?
Комбинации в пятимастном покере
| Рука | Комбинации | Вероятность | Формула |
| Пять одинаковых | 13 | 0.000002 | 13 |
| Прямой смыв | 50 | 0.000006 | 5*10 |
| Четыре одинаковых | 3900 | 0.000472 | 13*12* КОМБИНАЦИЯ (5,4)*5 |
| Румянец | 6385 | 0.000773 | 5*(COMBIN(13,5)-10) |
| Аншлаг | 15600 | 0.001889 | 13*12*COMBIN(5,3)*COMBIN(5,2) |
| Прямой | 31200 | 0.003777 | 10*(5^5-5) |
| Три одинаковых | 214500 | 0.025969 | 13*КОМБИН(12,2)*КОМБИН(5,3)*5^2 |
| Две пары | 429000 | 0.051938 | КОМБИН(13,2)*11*КОМБИН(5,2)^2*5 |
| Пара | 3575000 | 0.432815 | 13*КОМБИН(12,3)*КОМБИН(5,3)*5^3 |
| Ничего | 3984240 | 0.48236 | (COMBIN(13,5)-10)*(5^5-5) |
| Общий | 8259888 | 1 |
Обратите внимание, что я поменял местами фулл-хаус и флеш.
Сколько комбинаций из пяти карт в стандартной колоде игральных карт содержат карты ровно двух мастей?
Две масти могут быть разделены либо на 4 и 1, либо на 3 и 2. Давайте сначала рассмотрим разделение 4/1. Для масти с 4 картами есть 4 масти на выбор, а для масти с 1 картой — 3. Существует 715 способов выбрать 4 ранга из 13. Существует 13 способов выбрать один ранг. Таким образом, существует 4×3×715×13 = 111 540 способов получить разделение 4/1 между двумя мастями. По аналогичной логике, существует 4×3×combin(13,3)×combin(13,2) = 267 696 способов получить разделение 3/2. Таким образом, общая вероятность составляет (111540 + 267696) /combin(52,5) = 14,59%.
Каковы шансы получить карты 2-3-4-5-7 неподходящей масти? Большое спасибо, сайт отличный!
Спасибо. (4 5 -4)/combin(52,5) = 1020/2598960 = 1 из 2548.
На днях я был в Foxwoods и смотрел финальные два стола Foxwoods Poker Classic. Когда Винс Ван Паттен (один из ведущих World Poker Tour) пришёл посмотреть, он начал делать всевозможные пари с некоторыми из профессиональных игроков в покер, которые там находились. Он предлагал любому 20 к 1, если тот сможет перевернуть всю колоду карт, перебирая ранги и произнося вслух каждую карту: туз, двойка, тройка, четвёрка и так далее до короля, начиная снова с туза, так и не получив при этом карту, которую он объявляет. Никто не смог пройти весь путь, и Винс выиграл несколько сотен долларов примерно за 10 минут, прежде чем все сдались. Я знаю, что это должно быть возможно, но у меня есть подозрение, что Винс неплохо умеет мошенничать, предлагая всего 20 к 1. Каковы шансы действительно пройти всю колоду?
Простой способ оценить вероятность выигрыша — предположить, что каждая карта имеет вероятность 12/13 не совпадать с указанным рангом. Чтобы выиграть в этой ставке, жертве нужно было бы успешно сделать это 52 раза. Вероятность 52 выигрышей составляет (12/13) 52 = 1,56%. Справедливая цена составила бы 63,2 к 1. При соотношении 20 к 1 у Винса было преимущество в 67,3% (ой!).
По словам GM, который является лучшим математиком, чем я, фактическая вероятность составляет 1,6232727%. Причина разницы заключается в том, что результат каждого выбора положительно коррелирует с результатами предыдущих выборов.
Вчера вечером за столом один из игроков, старый, хитрый, неряшливый и агрессивный игрок, предложил всем сделать пари на равные шансы на флопе. Этот старый ворчун поставил на то, что одна из трех карт на флопе будет либо тузом, двойкой, либо валетом (иногда он менял три различимые карты). Каковы шансы на успех этой ставки? Ваша мудрость была бы очень кстати.
До того, как будут показаны какие-либо карты, вероятность того, что на флопе не появятся любые три ранга, составляет комбинация (40,3)/комбинация (52,3) = 9880/22100 = 44,71%. Таким образом, у этого парня было преимущество в 10,59%.
Предположим, из колоды в 52 карты раздают пять карт, и первая из них — король. Какова вероятность того, что выпадет хотя бы ещё один король? Я видел задачу про туз, которую вы решали, похожую на эту, но мне она показалась непонятной. Спасибо за любую помощь.
Для решения задач на вероятность я предпочитаю использовать комбинаторную функцию. Таким образом, существует 194 580 способов выбрать четыре карты, не являющиеся королями, из 48 некоролей в колоде. Существует 249 900 способов выбрать любые четыре карты из оставшихся 51 карты в колоде. Следовательно, вероятность того, что среди следующих четырех карт не окажется ни одного короля, составляет 194 580/249 900 = 77,86%. Таким образом, вероятность получить хотя бы один вид карт равна 100% - 77,86% = 22,14%.
Некоторые утверждают, что комбинаторная функция, вероятно, слишком сложна для понимания тех, кто задаёт подобные простые вопросы по теории вероятности. Я с этим согласен, но одна из главных причин создания этого сайта — попытка научить моих читателей чему-то новому в математике. Комбинаторная функция чрезвычайно полезна в теории вероятности и значительно экономит время. Однако на поставленный вопрос можно легко ответить и без неё.
Вероятность того, что вторая карта не король, составляет 48/51. Это потому, что в колоде осталось 48 карт, не являющихся королями, и всего 51 карта. Если вторая карта не король, то вероятность того, что третья карта также не король, составляет 47/50 (47 карт, не являющихся королями, деленные на 50 оставшихся карт). Исходя из этого, вероятность того, что ни одна из остальных четырех карт не является королем, составляет (48/51)×(47/50)×(46/49)×(45/48) = 77,86%. Вероятность того, что это не так, то есть хотя бы один король, составляет 100% - 77,86% = 22,14%.
Сначала выберите 5 карт из одной колоды из 52 карт. Затем сложите их значения в блэкджеке (T, J, Q, K = 10, A = 1). Какова вероятность того, что сумма будет четной/нечетной? Я думаю, что при избытке четных карт вероятность того, что сумма будет четной, будет намного выше.
Удивительно, но вероятность выпадения нечетного числа составляет 50,03%, несмотря на то, что 30 из 52 карт были четными. В следующей таблице показана вероятность каждого варианта распределения четных/нечетных карт.
Вопрос о четных и нечетных числах
| Равные | Шансы | Комбинации | Вероятность | Сумма |
| 0 | 5 | 15504 | 0.005965 | Странный |
| 1 | 4 | 155040 | 0.059655 | Даже |
| 2 | 3 | 565440 | 0.217564 | Странный |
| 3 | 2 | 942400 | 0.362607 | Даже |
| 4 | 1 | 719200 | 0.276726 | Странный |
| 5 | 0 | 201376 | 0.077483 | Даже |
| Общий | 2598960 | 1 |
Какова вероятность того, что из колоды вытянут три карты, ровно одна из них окажется пиковой мастью?
Вероятность того, что первая карта — пика, а две следующие — нет, составляет (13/52)×(39/51)×(38/50) = 14,53%. Затем следует умножить это на 3, поскольку пика может быть любой из трех карт. Таким образом, ответ: 3×14,53% = 43,59%. Для тех, кто предпочитает комбинаторную функцию, ответ: 13×combin(39,2)/ combin (52,3) = 9633/22100 = 43,59%.
Выберите два случайных числа от 0 до 1 (равномерно распределенных). Теперь выберите меньшее из них. Каково среднее значение выбранных чисел? А как насчет общего случая n чисел?
Для двух чисел ответ равен 1/3, а для n чисел — 1/(n+1). Решения я разместил на своей странице с математическими задачами , вопросы 194 и 195.
Вы играете в игру с участием трех человек: (а) вы сами, (б) ваш противник и (в) судья. Каждый из вас тайно выбирает действительное число от 0 до 1. После того, как все числа выбраны, они раскрываются. Побеждает тот игрок, чье число оказалось ближе всего к числу судьи, не превысив его. Если ваше число ближе, вы выигрываете 1 доллар. Если число вашего противника ближе, вы проигрываете 1 доллар. Если оба игрока превысили число судьи или игра заканчивается ничьей, игра заканчивается ничьей.
Существует ли число, которое можно выбрать таким образом, чтобы максимизировать ожидаемую прибыль, если другой игрок выбирает число случайным образом? А если у другого игрока тоже есть своя стратегия?
Надеюсь, вы довольны. Я потратил весь день на вторую часть, и мой ответ всё ещё был неверным. Чтобы не лишить своих читателей той же радости, я не буду просто так выкладывать ответы здесь. Я разделил задачу на две части и опубликовал ответы и решения на сайте mathproblems.info , задачи 196 и 197.
Если вы случайным образом выберете пять карт из стандартной колоды из 52 карт, какова вероятность того, что будут представлены все четыре масти?
Должно быть одно мастовое сочетание с двумя картами и три мастовых сочетания с одной картой в каждом. Для масти, представленной дважды, существует четыре возможных масти. Для масти, представленной дважды, существует комбинаций (13,2) = 78 способов выбрать 2 ранга из 13. Для каждой из трех других мастей существует по 13 возможных рангов. Таким образом, общее количество комбинаций составляет 4 × 78 × 13 × 13 × 13 = 685 464. Существует комбинаций (52,5) = 2 598 960 способов выбрать 5 карт из 52. Следовательно, вероятность составляет 685 464 / 2 598 960 = 26,37%.
Какова вероятность того, что любые два выбранных ранга, например, королева и король, появятся подряд в случайной колоде? Кто-то предложил мне поспорить на равные шансы, что это произойдет.
Согласно результатам случайного моделирования, вероятность составляет 48,64%. Поэтому я бы сделал это пари.
Можете ли вы порекомендовать функцию для сопоставления любых пяти карт из колоды в 52 карты с целым числом от 0 до 2 598 959?
Да. Сначала присвойте каждой карте значение от 0 до 51. Назовите карты c1–c5, расположив их в порядке убывания, начиная с c1 (наименьшее значение) и заканчивая c5 (наибольшее значение). Затем вызовите следующую функцию:
int GetIndex(int c1, int c2, int c3, int c4, int c5)
{
вернуть комбинацию(c5,5) + комбинацию(c4,4)+ комбинацию(c3,3) + комбинацию(c2,2) + комбинацию(c1,1);
}
Функция combin возвращает традиционное значение, за исключением случаев, когда первое значение меньше второго, в этом случае она возвращает 0, следующим образом:
int combin(int x, int y)
{
если (y>x)
вернуть 0;
еще
{
int i,n;
n=1;
для (i=x-y+1; i<=x; i++)
n*=i;
for (i=2; i<=y; i++)
н/=i;
вернуть n;
}
}
Если вы используете этот метод для доступа к элементу массива, загрузите массив следующим образом.
count=0;
для (c5 = 4; c5 < 52; c5++)
{
для (c4 = 3; c4 < c5; c4++)
{
для (c3 = 2; c3 < c4; c3++)
{
для (c2 = 1; c2 < c3; c2++)
{
для (c1 = 0; c1 < c2; c1++)
{
index_array[count]=WhateverYouWish;
count++;
}
}
}
}
}
Какова вероятность собрать 3 из 10 стрит-флешей, имея три карты в стрит-флеше с одним промежутком между ними?

Это задача, связанная с биномиальным распределением. Общая формула такова: если вероятность события равна p, и каждый исход независим, то вероятность того, что оно произойдет ровно w из t испытаний, равна комбинации (t,w)×p w ×(1-p) tw .
В данном случае есть 2 способа составить стрит-флеш. Вам нужна восьмерка бубен и еще одна карта либо шестерка, либо валет бубен. Существует 1081 комбинация из 47 оставшихся в колоде способов вытянуть 2 карты. Таким образом, вероятность получить стрит-флеш в любой раздаче составляет 2/1081 = 0,0018501. Вероятность получить 3 из 10 составляет 3 × (10,3) × (0,0018501) / ( 1 - 0,0018501) / ( 7 ) = 0,000000750178, или 1 из 1 333 017.
Две колоды по 54 карты (включая два джокера) перемешиваются вместе. Игроку дается половина колоды. Какова вероятность того, что игрок получил все четыре красные тройки?
В колоде 4 красные тройки и 104 другие карты. Получить все четыре красные тройки можно только одним способом. Существует комбинаций (104,50) = 1,46691 × 10²⁸ способов, которыми игрок может получить 50 из 104 других карт. Общее количество комбинаций равно combin(108,54) = 2,48578 × 10³⁰ . combin(104,50)/combin(108,54) = 0,059012.
Если вам не нравится работать с такими большими числами, вот альтернативное решение. Пронумеруйте четыре красные тройки от 1 до 4. Вероятность того, что первая красная тройка окажется в колоде игрока, составляет 54/108. Теперь уберите первую тройку. Вероятность того, что у игрока окажется вторая красная тройка, составляет 53/107, потому что у игрока осталось 53 карты, а всего карт 107. Аналогично, вероятность того, что у игрока окажется третья красная тройка, составляет 52/106, а четвертая красная тройка — 51/105. (54/108) × (53/107) × (52/106) × (51/105) = 0,059012.
Этот вопрос был поднят и обсужден на форуме моего дочернего сайта Wizard of Vegas .
В своей колонке от 14 декабря 2010 года вы написали, что комбинация AAAAAKK, которая специально упоминается в правилах казино, возможно, никогда не встречалась в истории игры. По словам другого дилера, игрок получил эту комбинацию на станции Мэйн-стрит в ноябре 2010 года.
Интересно. Как я уже писал, по моим оценкам, подобное событие происходит примерно раз в 23,7 года в любом месте штата Невада. Думаю, это был один из таких случаев.
Предположим, вы выбрали два ранга, например, короля и королеву. Какова вероятность того, что хотя бы один раз в случайно перемешанной колоде из 52 карт король и королева окажутся рядом?
У меня получается 48,6279%. Если вы хотите сделать ставку, то справедливые шансы на «да» составляют 1,0564 к 1.
Я слышал, что недавно состоялась «идеальная» партия в бридж, где каждый игрок получил по 13 карт одной из четырех мастей. Какова вероятность такого совпадения?
Также ходят слухи, что подобное произошло во время игры в вист в Уорикшире в 2011 году. Для пользы других читателей поясним: какова вероятность разделить колоду из 52 карт на четыре группы по 13 карт в каждой, причем каждая группа состоит исключительно из 13 карт одной из мастей.
Существует 53 644 737 765 488 800 000 000 000 000 возможных способов расположить 52 карты в четыре набора по 13 карт. 4! = 24 — это число выигрышных комбинаций, поскольку четыре масти можно распределить между четырьмя игроками любым удобным для вас способом. Таким образом, вероятность выигрыша равна 1 к 2 235 197 406 895 370 000 000 000 000. Для сравнения, если бы все 7,5 миллиарда человек на Земле раздавали карты в бридж со скоростью одна рука в секунду, вероятность того, что кто-то раздаст так называемую идеальную руку до взрыва Солнца через 5 миллиардов лет, составила бы 1 к 16 558.
Однако некоторые определяют «идеальную» комбинацию как ситуацию, когда один игрок получает все 13 карт любой масти. Я показываю, что вероятность этого составляет 1 к 39 688 347 497 играм. Вероятно, такое случается время от времени где-то на Земле.
Какова вероятность в техасском холдеме, что у двух игроков в одной раздаче окажется флеш, причём оба игрока используют свои карманные карты?
Для начала определим количество комбинаций карт игрока и игрового поля, при которых это может произойти. Очевидно, что существует четыре масти. Тогда существует combin(13,4)=715 способов выбрать четыре из 13 карт данной масти.
Во-вторых, это может произойти, если на доске находятся три карты одной масти, а две другие — среди остальных 39 карт. Существует 84 комбинации (9,3) = 84 способа, которыми на доске могут оказаться три из оставшихся 9 карт выбранной масти. Затем существует 741 комбинация (39,2) = 741 способ выбрать еще две карты из остальных 39 карт трех других мастей. Таким образом, существует 84*741 = 62244 способа, при которых на доске находятся три карты нужной масти.
В-третьих, еще один способ, как это может произойти, — это когда у игроков на столе лежат четыре карты одной масти, а вторая — среди остальных 39 карт. Существует 126 комбинаций (9,4) = 126 способов, которыми на столе могут оказаться четыре из 9 оставшихся карт выбранной масти. Затем есть 39 способов выбрать еще одну карту из остальных 39 карт трех других мастей. Однако не все из этих комбинаций приведут к тому, что оба игрока используют обе закрытые карты. Для выполнения этого условия на столе должна находиться младшая карта рассматриваемой масти. Вероятность этого из 8 карт этой масти, находящихся в игре, составляет 4/8 = 1/2. Таким образом, существует 126*39*(1/2) = 2457 способов, как на столе окажутся четыре карты рассматриваемой масти.
В-четвертых, последний способ, которым это может произойти, — это когда на столе лежат пять карт одной масти. Существует 126 комбинаций (9,5) = 126 способов, которыми на столе могут оказаться пять из 9 оставшихся карт выбранной масти. Однако не все из них приведут к тому, что оба игрока используют обе свои закрытые карты. Для выполнения этого условия на столе должны находиться две младшие карты рассматриваемой масти. Вероятность этого из 9 карт этой масти, находящихся в игре, составляет 10/36 = 5/18. Таким образом, существует 126*(5/18) = 35 способов, которыми на столе оказываются четыре карты рассматриваемой масти.
Таким образом, количество комбинаций, в которых это произойдет, составляет 715*(62244 + 2457 + 35) = 46286240.
Общее количество комбинаций способов выбрать четыре карты из 52, оставшихся на столе, и еще 5 из 48, равно combin(52,4)*combin(48,5) = 463 563 500 400.
Таким образом, вероятность составляет 46 286 240 / 463 563 500 400 = 0,000399395 = 1 к 2504.
Этот вопрос был задан и обсуждался на моём форуме, посвящённом игре Wizard of Vegas .
Крупье в казино работает над новым вариантом трехкарточного покера. Она берет все карты с картинками из стандартной колоды и тщательно перемешивает их. Затем она раздает 3 карты игроку №1, 3 карты игроку №2, 3 карты игроку №3 и последние 3 карты игроку №4. Какова вероятность того, что все четыре руки будут содержать стрит (JQK любой масти)?
[spoiler=Решение]
Раздавайте карты по одной за раз. Вероятность того, что первый игрок получит по одной карте каждого ранга, составляет 4^3/комбинация(12,3) = 64/220.
Предположим, первый игрок получил стрит. В колоде осталось по три карты каждого ранга. Вероятность того, что второй игрок получит по одной карте каждого ранга, составляет 3³/комбинация(9,3) = 27/84.
Предположим, что первые два игрока получили стрит. В колоде осталось по две карты каждого ранга. Вероятность того, что третий игрок получит по одной карте каждого ранга, составляет 2³/комбинация(6,3) = 8/20.
Предположим, что первые три игрока собрали стрит. В колоде остаётся по одной карте каждого ранга. Эти три карты, очевидно, образуют стрит.
Таким образом, вероятность того, что все четыре игрока соберут стрит, составляет (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3,74%.
[/спойлер]Этот вопрос задаётся и обсуждается на моём форуме Wizard of Vegas, начиная с этого сообщения .
Предположим, у меня есть колода из 48 карт, четыре масти, по двенадцать карт в каждой масти. Если я вытяну 15 карт, какова вероятность того, что я вытяну хотя бы одну карту из каждой масти?
Начнём со 100% и вычтем вероятности, при которых выпадет менее четырёх мастей.
Какова вероятность того, что, например, 48 карт не имеют червей? 36 карт не имеют червей. Количество способов выбрать 15 карт из 36 равно combin(36,15) = 5 567 902 560. Количество способов выбрать 15 карт из всех 48 равно 1 093 260 079 344. Таким образом, вероятность того, что 15 карт не имеют червей, равна 5 567 902 560 / 1 093 260 079 344 = 0,005093.
Далее умножим это на четыре, чтобы получить вероятность пропустить любую масть, а не только червы: 4 × combin(36,15)/combin(48,15) = 0,02037174.
Однако это приводит к двойному учету в некоторых ситуациях. Рассмотрим случай с 15 черными картами. В этом случае мы пропустим и червы, и бубны. Мы бы учли это дважды. Поэтому нам нужно это исправить. Существует combin(4,2) = 6 способов выбрать две масти из четырех. Вероятность того, что все 15 карт будут любых двух конкретных мастей, равна combin(24,15)/combin(48,15) = 1307504/1 093 260 079 344 = 0,00000120. Как уже упоминалось, существует шесть способов выбрать две масти из четырех, поэтому количество способов, при которых все карты будут двух мастей, равно 6 × combin(24,15)/combin(48,15) = 0,00000718.
Вычтя то, что мы посчитали дважды, мы получаем вероятность того, что будут представлены две или три масти, равную 0,02037174 - 0,00000718 = 0,02036456.
Обратите внимание, что нам не нужно беспокоиться о том, будет ли представлена только одна масть, поскольку невозможно выбрать 15 карт из 12.
В качестве заключительного шага вычтите вероятность выпадения 2 или 3 мастей из 100%, чтобы получить вероятность того, что будут представлены все четыре масти: 1,00000000 - 0,02037174 = 0,97963544.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Если я раздам 13 карт из перемешанной (предположительно случайной) колоды, сколько разных рангов я могу ожидать увидеть?
Это, безусловно, задача типа цепи Маркова.
В следующей таблице показано ожидаемое количество рангов с картами от 0 до 4 для всех чисел карт, сданных в колоду, от 1 до 52.
Ожидаемые ранги по розданным картам
| Карты | 0 рангов | 1 ранг | 2 ранга | 3 ранга | 4 ранга | Ожидал Ранги |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 13 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 25 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 26 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 27 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 28 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 29 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 30 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 32 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 34 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 35 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 36 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 37 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 38 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 39 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 42 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 44 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 47 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 48 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .
Кто-то предложил мне пари. Я должен выбрать любые три ранга из стандартной покерной колоды, записать свой прогноз, но держать его в секрете до конца. Например, 7-туз-2. Затем он предложил мне пари, что сможет назвать хотя бы один из моих рангов, если угадает три раза. Каковы были мои шансы на победу?
Чтобы выиграть, ваш противник должен ошибиться во всех трех прогнозах. Вероятность неверного первого прогноза составляет 10/13. Вероятность неверного второго прогноза — 9/12, поскольку мы можем исключить первый угаданный ранг из числа возможных вариантов. Вероятность неверного третьего прогноза — 8/11, поскольку мы можем исключить первые два угаданных ранга из числа возможных вариантов.
Для вашей победы должны произойти все три этих события. Таким образом, ваши шансы на победу составляют (10/13) * (9/12) * (8/11) = 720/1716 = 41,96%.
При равных шансах преимущество казино на этой ставке с вашей стороны составляет 16,08% (ой!).
Этот вопрос взят из книги Оуэна Э'Ши «Книга о пари на предложения» (номер 7).
Кто-то предложил мне пари: он должен был выбросить в сумме 12 очков двумя кубиками за 27 бросков. Если бы он этого не сделал, я бы выиграл равную сумму. Поскольку вероятность выпадения 12 составляет 1/36, разве ему в среднем не потребовалось бы 36 бросков, чтобы выбросить 12? Казалось бы, шансы были бы на моей стороне, если бы мой противник выбрасывал всего 27 очков. Прав ли я или в чем ошибка в моих расчетах?
Среднее время ожидания между выпадением 12 действительно составляет 36 бросков, включая сам бросок на 12. Однако это не означает, что они выпадают ровно каждые 36 бросков. Вероятность того, что НЕ выпадет 12, составляет (35/36). Вероятность того, что этого не произойдет за 27 бросков, составляет (35/36)^27. Таким образом, вероятность того, что хотя бы один раз выпадет 12, составляет 1-(35/36)^27 = 53,26%.
В следующей таблице показана вероятность выпадения как минимум 12 чисел при 20-36 бросках. Обратите внимание, что для получения преимущества при равных шансах необходимо 25 выпадений.
Вероятность 12
| Роллы | Вероятность |
|---|---|
| 20 | 43,07% |
| 21 | 44,66% |
| 22 | 46,19% |
| 23 | 47,69% |
| 24 | 49,14% |
| 25 | 50,55% |
| 26 | 51,93% |
| 27 | 53,26% |
| 28 | 54,56% |
| 29 | 55,82% |
| 30 | 57,05% |
| 31 | 58,24% |
| 32 | 59,40% |
| 33 | 60,53% |
| 34 | 61,63% |
| 35 | 62,69% |
| 36 | 63,73% |
Мы знаем, что существует 2 598 960 возможных комбинаций из пяти карт из 52. Мой вопрос: сколько возможных комбинаций из пяти карт можно составить из пяти колод?
Давайте разберемся с каждым типом рук по отдельности.
- Пять одинаковых карт: В колоде 52 разные карты, что составляет 52 комбинации.
- Четыре одинаковые карты: существует 52 возможных комбинации для четырех одинаковых карт и 51 для одной единственной карты. Таким образом, существует 52*51 = 2652 возможных комбинации для четырех одинаковых карт.
- Три одинаковые карты и две другие: существует 52 возможных комбинации для трех одинаковых карт и 51 для пары. Таким образом, существует 52*51 = 2652 возможных комбинации для фулл-хауса.
- Три одинаковые карты и две разные карты-одиночки: существует 52 возможных комбинации для трех одинаковых карт и combin(51,2)=1275 для двух карт-одиночек. Таким образом, существует 52*1275 = 66300 возможных комбинаций для тройки одинаковых карт.
- Две пары одинаковых карт и одна отдельная карта: существует combin(52,2)=1326 комбинаций для двух разных карт, образующих пары. Затем остается 50 комбинаций для отдельной карты. Таким образом, существует 1326*50=66300 возможных комбинаций для пары из двух карт.
- Одна пара одинаковых карт и три карты-одиночки: существует 52 возможных варианта пары. Тогда существует 20 825 комбинаций (51, 3) = 20 825 способов выбрать 3 карты из 51 оставшейся пары-одиночки. Таким образом, количество комбинаций для пары составляет 52 * 20 825 = 1 082 900.
- Пять отдельных карт: существует 2 598 960 способов выбрать пять карт из 52.
Сумма всех этих комбинаций составляет 3 819 816.
Этот вопрос задаётся и обсуждается на моём форуме, посвящённом игре Wizard of Vegas .


