Техасский холдем - Вероятность — общая
Каковы шансы получить две каре и стрит-флеш одному и тому же игроку в техасском холдеме с десятью игроками за 50 раздач?
Вероятность выпадения четырех одинаковых карт за семь карт составляет 0,00168067, а вероятность стрит-флеша — 0,00027851. Если x — вероятность выпадения четырех одинаковых карт, а y — вероятность стрит-флеша, то искомая вероятность равна combin(50,2)*48*x 2 *y*(1-xy) 47. Ответ равен 0,0000421845, или 1 к 23705.
Каковы статистические шансы собрать флеш в техасском холдеме? Легче ли собрать флеш в 7-карточном стаде или в холдеме, если играть за игрока?
Вы можете обратиться к моему разделу о вероятностях в покере, чтобы увидеть, что вероятность составляет 3,03%. Шансы одинаковы как в техасском холдеме, так и в 7-карточном стаде.
Каковы шансы собрать роял-флеш на ривере в техасском холдеме?
Для тех читателей, кто не знает, ривер — это пятая и последняя общая карта в техасском холдеме. Игрок должен составить лучшую покерную комбинацию из своих двух карт и пяти общих карт. Итак, вы спрашиваете, какова вероятность того, что игрок соберет роял-флеш из семи карт, и что седьмая сданная карта будет частью роял-флеша. Вероятность составления роял-флеша из 5 карт из 7 карт, до учета карт, составляет 4*combin(47,2)/combin(52,7) = 4324/133784560, или 1 к 30940. Вероятность того, что седьмая карта будет частью роял-флеша, составляет 5/7. Таким образом, окончательная вероятность составляет 21620/936491920, или 1 к 43316.
В техасском холдеме, каковы шансы собрать внутренний стрит с разницей в одну или две карты, начиная с пятой улицы и заканчивая флопом?
Для удобства читателей поясню: какова вероятность заполнить пробел в стрите (единица или двойка) двумя дополнительными картами, если в колоде осталось 47 карт? При наличии одного пробела вероятность равна 1-комбинация(43,2)/комбинация(47,2) = 0,164662. При наличии двух пробелов вероятность равна 4 2 /комбинация(47,2) = 0,0148.
В техасском холдеме, если все карты на флопе одной масти, какова вероятность того, что у любого игрока будет на руках еще две карты той же масти?
Осталось 10 карт одной масти, а в колоде — 49. Таким образом, вероятность равна combin(9,2)/combin(49,2) = 36/1176 = 0,0306.
В техасском холдеме и семикарточном стаде вероятности выпадения различных комбинаций одинаковы, или же они как-то различаются из-за общих карт? Могли бы вы объяснить, почему да или почему нет?
Да, вероятности одинаковы. Семь случайных карт из 52 имеют одинаковые шансы независимо от того, как они извлекаются из колоды или с кем вы ими делитесь.
Какова вероятность получить 7 рук с тузами, королями или лучше в холдеме за 35 раздач, исходя из первых двух карт?
Вероятность получения туза/короля составляет (8/52)*(4/51) = 0,012066. Вероятность получения любой пары составляет (3/51) = 0,058824. Таким образом, вероятность получения пары или лучшей комбинации равна 0,07089. Вероятность получения ровно семи комбинаций туза/короля или лучше равна combin(35,7)*(.07089)^7*(1-.07089)^28 = 0,00772. Чтобы вычислить вероятность получения 7 или более комбинаций, нам нужно будет пройтись по 7-35 комбинациям по одной. В сумме это составит 0,010366551.
Как рассчитать вероятность получения флеша из 4 карт или лучше на флопе в холдеме, если ваши карманные карты одномастные?
Вероятность получить еще 2 карты одной масти составляет 39 * combin(11,2) / combin(50,3) = 0,109439. Вероятность получить еще 3 карты одной масти составляет combin(11,3) / combin(50,3) = 0,008418. Таким образом, вероятность получить как минимум еще 2 карты одной масти составляет 0,117857.
Уважаемый гость! Прежде всего, хочу сказать, что у вас потрясающий сайт! Я читаю его уже довольно давно. Я проверил раздел вопросов по покеру и не нашел там этого вопроса. На другом сайте утверждается: «В Техасском Холдеме вероятность того, что на префлопе выпадет AK, а на ривере — A или K, составляет 1 к 2 (четное число)». Интуитивно это кажется слишком высоким показателем. Что вы думаете по этому поводу? Спасибо еще раз!
Спасибо вам тоже за добрые слова. Для тех, кто не знаком с холдемом, этот вопрос похож на вопрос: если игроку раздали туз и короля, а также пять случайных карт из оставшихся 50, какова вероятность того, что у игрока сложатся пара из короля и/или туза? Из остальных 50 карт 44 не являются королями или тузами. Количество способов вытянуть любые пять карт из 44 равно combin(44,5) = 1 086 088. Количество способов вытянуть любые пять карт из всех 50 равно combin(50,5) = 2 118 760. Таким образом, вероятность того, что туз и/или король не сложатся в пару, составляет 1086 088 / 2118 760 = 51,26%. Следовательно, вероятность того, что вы сложитесь в пару, составляет 1 - 51,26% = 48,74%. Это довольно близко к 1 к 2.
Какова вероятность того, что у двух игроков в техасском холдеме окажутся разные четыре одинаковые карты?
У двух игроков всего 9 карт. Они должны состоять из двух одинаковых карт и одной одиночной карты. Количество комбинаций для этого равно combin(13,2)*44 = 3432. Общее количество способов выбрать 9 карт из 52 равно combin(52,9) = 3 679 075 400. Таким образом, вероятность того, что у вас окажутся правильные карты, но не обязательно в правильном порядке, составляет 3432/3 679 075 400 = 1 из 1 071 992.
Однако, тот факт, что карты AAAABBBBC, не означает, что у обоих игроков будут разные каре. Количество способов составить из них комбинацию из 5 карт и двух комбинаций из 2 карт равно 9!/(5!*2!*2!) = 756. Ниже приведены способы, которыми могут выпасть эти 9 карт.
Четыре одинаковых комбинации с плохим исходом
Игрок 1 | Игрок 2 | Провал | Зеркальные узоры | Комбинации по шаблону | Полные комбинации |
АА | ББ | AABBC | 2 | 72 | |
АА | АБ | АБББК | 4 | 48 | 192 |
АА | АА | BBBBC | 2 | 6 | 12 |
АА | кондиционер | АББББ | 4 | 12 | 48 |
АА | до н.э. | AABBB | 4 | 24 | 96 |
АБ | АБ | AABBC | 1 | 144 | 144 |
АБ | кондиционер | AABBB | 4 | 48 | 192 |
Из этих комбинаций только первая и пятая приводят к тому, что у обоих игроков оказываются разные четыре одинаковые карты. Таким образом, вероятность того, что набор карт AAAABBBBC приведет к двум разным четырем одинаковым картам, составляет 168/756 = 22,22%.
Таким образом, ответ на ваш вопрос: (3432/3 679 075 400) * (168/756) = 1 из 4 823 963. Если говорить о более практичных вещах, то в Party Poker есть джекпот за проигрышную комбинацию из четырех восьмерок. Учитывая, что есть две одинаковые карты, вероятность того, что обе будут восьмерками или больше, составляет combin(7,2)/combin(13,2) = 21/78 = 26,92%. Таким образом, вероятность того, что любая раздача двух игроков приведет к этому джекпоту за проигрышную комбинацию, составляет 1 из 17 917 577.
Вчера вечером один игрок предложил мне пари в техасском холдеме. Он сказал, что на флопе появится как минимум одна картинка (или любые три ранга), и предложил равные шансы. Стоило ли мне принять ставку?
Количество способов выбрать 3 карты из 40 некарточных равное числу равно (40*39*38)/(1*2*3) = 9880. Количество способов выбрать 3 карты из 52 равно (52*51*50)/(1*2*3) = 22100. Таким образом, вероятность не получить карту с изображением равна 9880/22100 = 44,71%. Следовательно, вероятность получить карту с изображением равна 55,29%. Его сторона в пари имела преимущество в 10,58%.
Играем в техасский холдем с 10 игроками, используя стандартную колоду из 52 карт. После раздачи первых двух карт каждому игроку, какова вероятность того, что на флопе (следующие три карты) будут карты одной масти? Имеет ли значение, если у меня на руках обе карты одной масти и/или у каждого игрока карты разной масти?
Прежде чем рассматривать свои карты, вероятность составляет 4× комбинация (13,3)/комбинация (52,3) = 5,1764706%.
Иными словами, вероятность того, что вторая карта во флопе совпадет с первой по масти, составляет (12/51). Вероятность того, что третья карта во флопе совпадет с ней, составляет (11/50). (12/51) × (11/50) = 5,1764706%.
Вероятность немного меняется, если учесть ваши собственные карты. Если у вас две карты одной масти, то вероятность выпадения флеша одной масти равна pr(флеш одной масти) + pr(флеш другой масти) = combin(11,3)/combin(50,3) + 3×combin(13,3)/combin(50,3) = 5,2193878%.
Если у вас две карты разных мастей, то вероятность выпадения одной масти на флопе равна pr(флеш общей масти) + pr(флеш другой масти) = 2×combin(12,3)/combin(50,3) + 2×combin(13,3)/combin(50,3) = 5,1632653%.
Дорогой волшебник, как бы мне хотелось обладать твоими мозгами. В любом случае, мои проблемы со статистикой продолжаются. Я пытаюсь придумать формулу для расчета вероятности получения флеша на флопе, терне и ривере (техасский холдем) в зависимости от того, одномастные у меня карты или нет. Я пробовал C(50,2) / C(47,5), но это не сработало для одномастной пары на ривере... Надо было мне внимательнее учиться в школе! Спасибо! Твой самый большой поклонник
Спасибо за добрые слова, но я не настолько умён. Пару лет назад я сдавал вступительный экзамен в Mensa и не вошёл в необходимые 2% лучших. Я до сих пор расстроен, что они отказались сказать мне, насколько хорошо я справился. 13 января в Вегасе пройдут отборочные испытания в Jeopardy, на которые у меня назначена встреча, и я уверен, что и там я провалюсь. В общем, вот ответ на ваш вопрос:
С одномастными карманными картами:
Флеш после флопа: комбинация (11,3)/комбинация(50,3) = 165/19600 = 0,842%.
Флеш после терна: (комбинация(11,2)*39/комбинация(50,3))*(9/47) = 2,096%.
Флеш после ривера: (combin(11,2)*combin(39,2)/combin(50,4))*(9/46) = 3,462%.
При наличии несовпадающих карманных карт:
Флеш после флопа: 0%
Флеш после терна: 2*комбинация(12,4)/комбинация(50,4) = 0,430%.
Флаш после реки: (2*combin(12,3)*39/combin(50,4))*(9/46) = 1,458%.
Вот коммуативные вероятности.
С одномастными карманными картами:
Флеш на флопе: 0,842%.
Смыв по очереди: 2,937%.
Промыв реки: 6,400%.
При наличии несовпадающих карманных карт:
Флеш на флопе: 0,000%
Смыв по очереди: 0,430%.
Промыв реки: 1,888%.
Привет, Wizard! Прежде всего, хочу сказать, что мне очень нравятся твои точные, без лишних деталей, ответы. Итак, если карманные карты в Холдеме — AA, а на флопе — KQ9, какова вероятность собрать фулл-хаус? Я над этим работаю уже целую вечность :( и до сих пор не нашел ответа, которому мог бы доверять.
Фулл-хаус можно собрать из туза и короля, дамы или девятки. Осталось 2 туза и по 3 короля, дамы и девятки. Таким образом, существует 2*3*3=18 таких комбинаций. Единственный другой вариант — пара король, дама или девятка. Существует 3*комбинация(3,2)=9 таких комбинаций. Общее количество комбинаций равно 47*46/2 = 1081. Следовательно, вероятность составляет (18+9)/1081 = 2,50%.
Я ваш большой поклонник уже много лет (ещё до того, как вы заинтересовались покером и ставками на спорт) и с нетерпением ждал каждой колонки «Спроси волшебника». Здорово, что вы снова их публикуете! Мой вопрос вот в чём: в моём местном покерном клубе в определённые часы действует акция «Тузы взломаны, выиграй пачку фишек». То есть, если у вас карманные тузы в одной из их игр в Техасский Холдем 3-6 или 4-8, и вы проигрываете банк, казино даёт вам пачку фишек (100 долларов). Я пытаюсь понять, как часто а) у меня выпадают карманные тузы, б) как часто я проигрываю, если играю агрессивно, как положено, и в) не лучше ли просто чекать до конца и надеяться на проигрыш, ведь 100 долларов обычно больше, чем был бы банк в любом случае. Любая статистика, которой вы можете поделиться, была бы замечательной и очень ценной! Ещё раз спасибо и продолжайте просвещать людей!
Спасибо за добрые слова. Вероятность получить карманные тузы в любой раздаче составляет 6/1326, или один раз на 221 раздачу. Согласно моему разделу о техасском холдеме на 10 игроков (/games/texas-hold-em/10players.html), вероятность выигрыша с карманными тузами составляет 31,36%, при условии, что все игроки доиграют до конца. Однако это большое «если». Если бы меня заставили сделать предположение, я бы оценил вероятность выигрыша с тузами в реальной игре на 10 игроков примерно в 70%. Таким образом, вероятность получить карманные тузы и проиграть составляет 0,3*(1/221) = 0,1357%. Следовательно, при стоимости 100 долларов за раздачу это составляет 13,57 центов за раздачу. При участии более десяти человек это обходится покер-руму в среднем в 1,36 доллара за раздачу, что значительно уменьшает рейк. Я склонен согласиться с вашей стратегией колла, которая позволит удержать в раздаче больше игроков и увеличит ваши шансы на проигрыш.
Прежде всего, хочу поблагодарить вас за замечательный сайт. Теперь мой вопрос: мы играем в техасский холдем, и на флопе у нас флеш-дро с двумя младшими картами. Мы все знаем процент вероятности собрать флеш, но нас интересует процент выигрыша раздачи. Допустим, мы уверены, что у кого-то на руках карта старше нас. Так вот, мой вопрос: каков процент вероятности того, что на руках окажется только одна карта этой масти, а не две? С уважением.
Пожалуйста. Итак, у вас четыре карты для флеша, а после флопа на борде две. Вероятность получить ровно одну карту нужной масти составляет 9*38 / комбинация (47,2) = 342/1081 = 31,64%.
В техасском холдеме я хотел бы узнать вероятность того, что другому игроку могли выпасть две одномастные карты, позволяющие составить флеш старше моей, если на ривере ровно 3 одномастные общие карты. Например, если у меня 89 пик, а общие карты включают 3, 7 и короля пик, то в колоде на 4 пики больше моей девятки (TJQA). Какова вероятность того, что кому-то выпала рука с двумя пиками, включая хотя бы одну из старших пик (при игре за 9 игроков)? А если только 2 (или 3, или x) пики больше моей самой старшей закрытой карты? Спасибо за помощь и за отличный сайт.
В следующей таблице показана вероятность для 1–8 игроков более высоких рангов и 2–10 игроков, включая вас. В вашем примере с 4 игроками более высоких рангов и 9 игроками в общей сложности вероятность составляет 16,45%. При расчете этих вероятностей я исходил из предположения о независимости раздач, что не является правильным предположением, но результаты должны быть достаточно точными.
Вероятность старшего флеша. Более высокие ранги (внизу) по общему количеству игроков (по горизонтали). Оценка Волшебника.
| Высшие звания | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,71% | 1,41% | 2,11% | 2,80% | 3,49% | 4,17% | 4,85% | 5,52% | 6,19% |
| 2 | 1,31% | 2,61% | 3,89% | 5,15% | 6,40% | 7,62% | 8,84% | 10,03% | 11,22% |
| 3 | 1,82% | 3,60% | 5,36% | 7,08% | 8,77% | 10,43% | 12,05% | 13,65% | 15,22% |
| 4 | 2,22% | 4,40% | 6,52% | 8,60% | 10,63% | 12,61% | 14,56% | 16,45% | 18,31% |
| 5 | 2,53% | 4,99% | 7,39% | 9,72% | 12,00% | 14,23% | 16,39% | 18,50% | 20,56% |
| 6 | 2,73% | 5,38% | 7,96% | 10,47% | 12,91% | 15,29% | 17,60% | 19,85% | 22,03% |
| 7 | 2,83% | 5,58% | 8,25% | 10,84% | 13,36% | 15,81% | 18,20% | 20,51% | 22,76% |
| 8 | 2,83% | 5,58% | 8,25% | 10,84% | 13,36% | 15,81% | 18,20% | 20,51% | 22,76% |
Вероятность старшего флеша. Более высокие ранги (внизу) по общему количеству игроков (по горизонтали). Моделирование Miplet.
| Высшие звания | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0,69% | 1,41% | 2,12% | 2,83% | 3,54% | 4,25% | 4,96% | 5,66% | 6,36% |
| 2 | 1,28% | 2,60% | 3,91% | 5,21% | 6,48% | 7,77% | 9,05% | 10,31% | 11,56% |
| 3 | 1,79% | 3,61% | 5,41% | 7,19% | 8,92% | 10,68% | 12,41% | 14,11% | 15,79% |
| 4 | 2,19% | 4,40% | 6,58% | 8,75% | 10,85% | 12,94% | 15,01% | 17,04% | 19,04% |
| 5 | 2,50% | 5,00% | 7,47% | 9,92% | 12,28% | 14,63% | 16,94% | 19,21% | 21,43% |
| 6 | 2,71% | 5,40% | 8,06% | 10,69% | 13,23% | 15,74% | 18,23% | 20,65% | 23,03% |
| 7 | 2,81% | 5,61% | 8,36% | 11,08% | 13,70% | 16,30% | 18,86% | 21,37% | 23,82% |
| 8 | 2,81% | 5,61% | 8,36% | 11,08% | 13,70% | 16,30% | 18,86% | 21,37% | 23,82% |
Отличный сайт. Спрашиваю это для себя лично. Я играл в техасский холдем вчетвером. Мне раздали карманные тузы. На ривере у меня выпал роял-флеш. Интересно, каковы шансы собрать роял-флеш на ривере, имея тузы в начале?
Спасибо. Предположим, что роял состоит из одного из ваших двух тузов. Количество способов составить роял к риверу составляет 2*46=92. Это будут две масти ваших карманных тузов и 46 вариантов для дополнительной карты. Существует комбинаций (50,5) = 2 118 760 способов раздать 5 карт из 50. Таким образом, вероятность составляет 92/2 118 760 = 1 из 23 030.
Если на флопе выпадают три карты одной масти, а у меня нет карты той же масти, что и на флопе, и за столом осталось десять игроков, какова вероятность того, что у кого-то флеш?
Вероятность того, что у любого игрока будет флеш, составляет combin (11,2)/combin(49,2) = 55/1176 = 4,68%. Предполагая независимость между раздачами, что не так, вероятность того, что у 9 игроков не будет флеша, составляет (1 − 0,0468%) 9 = 64,98%. Таким образом, вероятность того, что хотя бы у одного игрока будет флеш, составляет 1-0,6498 = 35,02%. Это всего лишь быстрая оценка. Если бы я провел случайное моделирование, я думаю, вероятность была бы немного выше из-за зависимости между раздачами.
Уважаемый господин Волшебник, я недавно пытался рассчитать вероятность получения флеша в Техасском Холдеме, если мне раздали две одномастные карты на руках? Мой ответ постоянно получается 5,8%, но это кажется неправильным. Буду очень благодарен за вашу помощь. Спасибо.
Вероятность собрать флеш, имея ровно три карты той же масти, что и ваши карманные карты, равна combin (11,3)×combin(39,2)/combin(50,5) = 122265/2598960 = 0,057706. Вероятность собрать флеш, имея на четыре карты больше той же масти, что и ваши карманные карты, равна combin(11,4)×combin(39,1)/combin(50,5) = 2145/2118760 = 0,001012. Вероятность собрать флеш, имея на пять карт больше той же масти, что и ваши карманные карты, равна combin(11,5)/combin(50,5) = 462/2118760 = 0,000218. Вероятность собрать флеш на борде в другой масти равна 3×combin(13,5)/combin(50,5) = 3861/2118760 = 0,001822. Сложив все это, получаем 0,057706 + 0,001012 + 0,000218 + 0,001822 = 0,060759.
Какова вероятность увидеть «разбитую доску» в Техасском Холдеме? То есть, пять карт на доске, где нет пары, флеш и стрит невозможны.
Количество комбинаций пяти различных рангов на доске равно (13,5)*4 5 = 1287 × 1024 = 1 317 888.
Вероятность того, что эти пять рангов будут представлять три масти, две пары и одну единицу, равна combin(4,2)*2*combin(5,2)*combin(3,2)=360. Combin(4,2) — это количество способов выбрать две масти из четырех для мастей, представленных дважды. 2 — это два способа выбрать масть, представленную один раз. Combin(5,2) — это количество способов выбрать два ранга из пяти для первой масти из двух карт. 4 5 — это количество способов выбрать два ранга из трех оставшихся для другой масти из двух карт.
Вероятность того, что эти пять рангов будут представлять четыре масти, одну из двух и три из одной, равна 4*комбинация(5,2)*3*2=240. 4 — это количество способов выбрать одну масть из четырех для мастей, представленных дважды. Комбинация(5,2) — это количество способов выбрать два ранга из пяти для этой масти из двух карт. 3 — это количество способов выбрать один ранг из трех оставшихся для первой масти из одной карты. 2 — это количество способов выбрать один ранг из двух для второй масти из одной карты.
Существует 4⁵ = 1024 способа расположить четыре масти на пяти разных рангах.
Таким образом, вероятность того, что будет присутствовать не более двух карт одной масти, составляет (360+240)/1024 = 600/1024 = 58,59%.
Существует 1287 комбинаций (13, 5) = 1287 способов расположить 5 рангов из 13. Число таких комбинаций, в которых никакие три ранга не находятся в пределах диапазона 5, равно 79. Простой формулы для этого нет. Мне пришлось перебрать каждую комбинацию. Таким образом, вероятность того, что ранги будут достаточно разнесены, составляет 79/1287 = 6,14%.
Таким образом, вероятность поломки доски составляет (1317888/2596960)*(600/1024)*(79/1287) = 1,825211%.
Меня спросили о количестве сломанных стритов. Вот список всех 79 возможных.
| 2378Q 2378K 2379Q 2379K 237TQ 237TK 237JQ 237JK 237QK 2389K 238TK 238JK 238QK 2479Q 2479K 247TQ 247TK 247JQ 247JK 247QK | 2489K 248TK 248JK 248QK 257TQ 257TK 257JQ 257JK 257QK 258TK 258JK 258QK 267JQ 267JK 267JA 267QK 267QA 267KA 268JK 268JA | 268QK 268QA 268KA 269JA 269QA 269KA 278QK 278QA 278KA 279QA 279KA 289KA 3489K 348TK 348JK 348QK 358TK 358JK 358QK 368JK | 368JA 368QK 368QA 368KA 369JA 369QA 369KA 378QK 378QA 378KA 379QA 379KA 389KA 469JA 469QA 469KA 479QA 479KA 489KA |
Я играю в Техасский Холдем в Caesars Indiana. Там есть джекпот за плохую раздачу, который теперь составляет четыре карты или больше. Оба игрока должны разыграть обе свои карманные карты, и карты должны быть розданы четырем игрокам. Мой вопрос: какова вероятность того, что любая раздача окажется плохой, при условии, что все игроки останутся до конца?
В моем новом разделе «Джекпот за неудачную раздачу» показано, что вероятность такой неудачной раздачи в игре с 10 игроками составляет 0,0000108, или примерно 1 к 93 000.
Почему в вашей таблице возврата в Ultimate Texas Hold 'Em рекомендуется крупный рейз для двухкарточных комбинаций, в которых ожидаемый возврат отрицательный? Например, одномастные K/2.
Согласно моим расчетам вероятностей в техасском холдеме для двух игроков , при мастях K/2 возможны следующие исходы:
Победа 51,24%
Потерять 44,82%
Ничья 3,94%
В моей таблице по игре Ultimate Texas Hold 'Em показано, что игрок имеет преимущество на ставке Play, но находится в невыгодном положении на ставках Ante и Blind. В этом случае у игрока плохие шансы на Ante и Blind. Однако его шансы на Play благоприятны. Таким образом, сделав максимальное повышение ставки, он получает максимальную выгоду от своих шансов на выигрыш, превышающих 50%. Плохие шансы на двух других ставках снижают общую выгоду до менее 50%. Эта выгода была бы еще меньше при меньшем повышении ставки.
В Мировой серии покера 2008 года каре тузов Мотоюки Мабучи было обыграно роял-флешем Джастина Филлипса. У меня простой вопрос о вероятности такого исхода. ESPN и другие источники указывают вероятность 1 к примерно 2,7 миллиардам. Мне кажется, они просто взяли опубликованные вероятности выпадения каре и умножили их на вероятность выпадения роял-флеша. Правильный ли это метод расчета?
Я тоже не согласен с цифрой 1 к 2,7 миллиардам. Как вы сказали, они, похоже, рассчитывали вероятности независимо для каждого игрока, только для случая, когда оба игрока используют обе закрытые карты, и умножали их. Используя этот метод, я получаю вероятность 0,000000000341101, или примерно 1 к 2,9 миллиардам. Возможно, цифра 1 к 2,7 миллиардам также включает в себя ошибку округления вероятностей для обоих игроков. Они также, очевидно, забыли умножить вероятность на 2, по причинам, которые я объясню позже.
Существует три способа, которыми четыре туза могут проиграть роял-флешу, а именно:
Вариант 1: У одного игрока две карты для роял-флеша, у другого — два туза, а на столе находятся ещё два туза, ещё две карты для роял-флеша и любая другая карта.
Пример:
Игрок 1:

Игрок 2:

Доска: 




В большинстве покер-румов, чтобы претендовать на джекпот за «плохую раздачу», и выигрывающий, и проигравший игрок должны использовать обе свои закрытые карты. Именно такая «плохая раздача» была показана в видео; фактически, это были именно те карты.
Вариант 2: У одного игрока две карты для роял-флеша (TK), у другого — один туз и «пустая» карта, а на столе находятся остальные три туза и две карты для роял-флеша.
Пример:
Игрок 1:

Игрок 2:

Доска: 




Вариант 3: У одного игрока есть одна карта для роял-флеша (TK) и пустая карта, у другого — два туза, а на столе находятся еще два туза и три карты для роял-флеша.
Пример:
Игрок 1:

Игрок 2:

Доска: 




В следующей таблице показано количество комбинаций для каждого случая как для игроков, так и для доски. В нижней правой ячейке указано общее количество комбинаций, равное 16 896.
Комбинации неудачных бросков
| Случай | Игрок 1 | Игрок 2 | Доска | Продукт |
|---|---|---|---|---|
| 1 | 24 | 3 | 44 | 3168 |
| 2 | 24 | 132 | 1 | 3168 |
| 3 | 704 | 3 | 1 | 2112 |
| Общий | 8448 |
Однако, даже если бы мы поменяли местами карты двух игроков, всё равно получилась бы неудачная комбинация. Поэтому нам следует умножить количество комбинаций на 2. С учётом этого, общее количество подходящих комбинаций составляет 2 × 8448 = 16896.
Общее количество всех комбинаций в Техасском Холдеме для двух игроков составляет combin (52,2) × combin(50,2) × combin(48,5) = 2 781 381 002 400. Таким образом, вероятность проигрыша четырех тузов роял-флешу составляет 8448/2 781 381 002 400 = 0,0000000060747, или примерно 1 к 165 миллионам. Вероятность простого случая «плохой победы» составляет 1 к 439 миллионам. Простая причина, по которой шансы не так велики, как показано в этом видео, заключается в том, что эти две руки перекрываются, и туз является общим. Другими словами, эти два события положительно коррелируют.
Вы абсолютно правы, согласно статье «Правда о нью-йоркском видеопокере» . Исход игры действительно предопределен. Независимо от того, какие карты игрок оставляет себе, он не может избежать своей участи. Если игрок намеренно пытается избежать своей участи, игра использует функцию «ангела-хранителя», чтобы исправить ошибку игрока. Я полностью согласен с автором в том, что такие игры должны предупреждать игрока о том, что он играет не в настоящий видеопокер, а таблица выплат является бессмысленным показателем реальных шансов игрока. Следует также отметить, что подобные поддельные видеопокерные автоматы встречаются не только в Нью-Йорке.
Здравствуйте, я семиклассник из Гавайев. Я делаю проект для научной ярмарки, посвященный покеру и перетасовке карт. Я использую ваши диаграммы, показывающие процент выигрыша карманных комбинаций в техасском холдеме в зависимости от количества игроков в игре. Я надеюсь, вы сможете ответить на несколько вопросов, которые помогут мне в моем проекте:
- Как вы получили процентные значения, представленные на диаграммах?
- Если вы использовали компьютерную программу, как вы её разработали и сколько времени это заняло?
- Вы заявили, что начали вести «Волшебника шансов» как хобби. Изменился ли ваш подход к экспериментам по мере того, как сайт становился более известным? Почему да или почему нет?
- Для игры вдвоем использовалась программа с циклическим перебором, которая перебирала все 1225 возможных карт противника и 1 712 304 возможных общих карт. Для игры втроем или ввосьми игроков циклический перебор занял бы непомерно много времени, поэтому я использовал случайное моделирование.
- Я пишу почти все свои программы на C++, включая две упомянутые выше. Остальные написаны на Java или PERL. В основном я копирую и вставляю код из других программ, связанных с покером. На написание нового кода ушло всего около дня.
- Да, я создал свой сайт как хобби в июне 1997 года. Только в январе 2000 года я начал размещать рекламу и попытался превратить это в бизнес. За эти годы сайт сменил три домена. Вот как он выглядел в мае 1999 года . Цель сайта всегда оставалась неизменной: ресурс по математически обоснованным стратегиям азартных игр. С годами я просто добавлял новые игры и материалы. Один из экспериментов заключался в публикации моих прогнозов на сезон НФЛ 2005 года , который закончился полным провалом.
Привет, Волшебник. Я прочитал твои вопросы по Техасскому Холдему и заметил, что ты рассчитал вероятность увидеть туз или короля на столе, имея карманные дамы, в 59,85%. Как ты получил эту цифру?
Из оставшихся 50 карт в колоде существует комбинаций (50,5) = 2 118 760, состоящих из пяти карт. 42 из этих карт — это 2-Q. Количество комбинаций из 5 карт из 42 равно комбинации (42,5) = 850 668. Таким образом, вероятность не получить короля или туза составляет 850 668 / 2 118 760 = 40,15%. Следовательно, вероятность получить хотя бы один туз или короля составляет 1 - 40,15% = 59,85%.
Альтернативный расчет: 1 - pr(первая карта на флопе не туз или король) × pr(вторая карта на флопе не туз или король) × pr(третья карта на флопе не туз или король) × pr(четвертая карта на флопе не туз или король) × pr(пятая карта на флопе не туз или король) = 1 - (42/50) × (41/49) × (40/48) × (39/47) × (38/46) = 59,85%.
Имея две одномастные карты в техасском холдеме, каковы мои шансы получить ровно две дополнительные карты той же масти на флопе?
Существует 55 комбинаций (11,2) = 55 способов получить еще две карты одной масти и 39 способов получить карту другой масти. Всего существует 19 600 возможных комбинаций карт на флопе. Таким образом, вероятность получить ровно четыре карты для флеша после флопа составляет 55 × 39 / 19 600 = 10,94%.
Я участвовал в онлайн-покерной раздаче и хотел бы узнать вероятность такого исхода, пожалуйста:
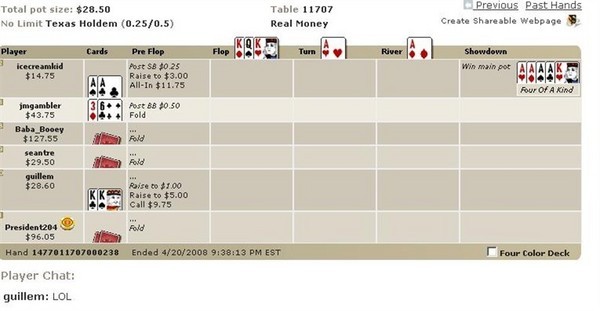
Обычно меня уже тошнит от вопросов на выбывание, но этот был слишком болезненным, чтобы его игнорировать. До раздачи первой карты вероятность того, что четыре короля будут побеждены четырьмя тузами в игре для двух игроков, у которых у обоих игроков есть карманные пары, составляет 2* комбинация (4,2)*комбинация(4,2)*44/(комбинация(52,2)*комбинация(50,2)*комбинация(48,5)) = 2*6*6*44/(1326*1225*1712304) = 1 из 877 961 175. Это была игра для шести игроков, поэтому комбинаций (6,2) = 15 различных пар игроков. В игре для шести игроков вероятность в 15 раз выше, или 1 из 58 530 745. После раздачи указанных карманных карт и до флопа вероятность того, что раздача завершится так, как это произошло, составляет 1 к 38 916.
В одном из карточных клубов Лас-Вегаса проходит акция: соберите флеш во всех четырех мастях и получите 400 долларов. Необходимо использовать обе свои карманные карты, время ограничено пятью часами. Предположим, что раздача длится 35 раздач в час, и отсчет времени начинается с первого флеша. Какова вероятность собрать остальные три флеша в течение пяти часов? Спасибо.
Допустим, ваш первый флеш — пики. При скорости 35 раздач в час, за пять часов можно сыграть 175 раздач. Таким образом, у вас есть 175 раздач, чтобы собрать флеш в червах, бубнах и трефах. Я буду исходить из того, что игрок никогда не сбрасывает карты, если есть вероятность собрать флеш в одной из необходимых ему мастей.
Вероятность флеша определенной масти, скажем, червей, с использованием обеих карманных карт равна combin(13,2)×[combin(11,3)×combin(39,2) + combin(11,4)×39 + combin(11,5)]/(combin(52,2)×combin(50,5)) = 10576566/2809475760=0.003764605. В следующих 175 раздачах вероятность пропустить флеш червей составит (1-0.003764605) 175 =0.51682599.
Было бы неправильно говорить, что вероятность не собрать остальные три масти равна pr(нет флеша червей) + pr(нет флеша бубен) + pr(нет флеша треф), потому что вы удвоите вероятность не собрать две из них. Поэтому следует добавить pr(нет флеша червей или бубен) + pr(нет флеша червей или треф) + pr(нет флеша треф или бубен). Однако это приведет к ошибочному вычитанию вероятности не собрать все три флеша. Поэтому следует добавить pr(нет флеша треф, бубен или червей).
Вероятность того, что за 175 раздач ни разу не выпадут карты одной из двух конкретных мастей, составляет (1-2×0,003764605) 175 =0,266442448.
Вероятность того, что за 175 раздач ни разу не останется ни одной из трех мастей, составляет (1-3×0.003764605) 175 =0.137015266.
Таким образом, ответ равен 1-3×0,51682599 + 3×0,266442448 - 0,137015266 = 0,111834108.
Хочу поблагодарить dwheatley за помощь в решении этой проблемы. Она обсуждается на моём форуме Wizard of Vegas .
Дойл Брансон прославился тем, что выиграл Главный турнир Мировой серии покера в 1976 и 1977 годах. Оба раза у него на руках были карты 10-2, и оба раза на ривере он собрал фулл-хаус. Какова вероятность такого исхода?
При наличии двух карт разных рангов вероятность составления фулл-хауса составляет 1 к 121,6. Вероятность составления фулл-хауса на ривере составляет 1 к 207.
Вероятность собрать такую комбинацию на ривере дважды из двух составляет 1 к 43 006.
Вероятность того, что это произойдет с двумя одинаковыми стартовыми картами, только по рангу, составляет 1 к 3 564 161.
Вероятность того, что это произойдет ровно при соотношении 10 к 2 в обоих случаях, составляет 1 к 295 379 826.
Только что вернулся с покерного вечера в ветеранской организации. Три раза подряд получил 6-6 в кармане! Никогда раньше такого не случалось. Какова вероятность получить карманную пару одинакового ранга три раза подряд за вечер? Можно предположить, что вечер состоит из 120 раундов.
Ответ и решение находятся под спойлером.
[спойлер]В любой момент времени вы можете находиться в четырех возможных состояниях:
- Состояние 1: Первая рука или любая рука, в которой последняя рука не была карманной парой.
- Состояние 2: Последняя раздача — карманная пара.
- Состояние 3: Последние две руки состояли из одной и той же карманной пары.
- Состояние 4: Уже получено три одинаковые пары карманных карт подряд.
Если вы находитесь в состоянии 1, вы можете перейти в состояние 2 с вероятностью 3/51. В противном случае вы остаетесь в состоянии 1.
Если вы находитесь во втором состоянии, вы можете перейти в третье состояние с вероятностью (4/52)×(3/51). В противном случае вы возвращаетесь в первое состояние.
Если вы находитесь в состоянии 3, вы можете перейти в состояние 4 с вероятностью (4/52)×(3/51). В противном случае вы возвращаетесь в состояние 1.
Если вы находитесь в штате 4, вы остаётесь там.
При этом матрицу переходов T можно создать следующим образом:
| 0.941176 | 0.058824 | 0.000000 | 0.000000 |
| 0.941176 | 0.054299 | 0,004525 | 0.000000 |
| 0.941176 | 0.054299 | 0.000000 | 0,004525 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
Всего было сыграно 120 раздач, поэтому найдите T^120.
| 0.941044 | 0.058549 | 0.000265 | 0.000141 |
| 0.941025 | 0.058548 | 0.000265 | 0.000162 |
| 0.936786 | 0.058284 | 0.000264 | 0.004666 |
| 0.000000 | 0.000000 | 0.000000 | 1.000000 |
В верхней правой ячейке показана вероятность того, что, начав с состояния 1, мы перейдем в состояние 4 после 120 стартовых раздач в последовательности из трех раздач, которая составляет 0,000141471.
Возьмем обратное этому числу значение, вероятность составит 1 к 7068,605131.
[/spoiler]Этот вопрос поднимается и обсуждается на моём форуме в Wizard of Vegas .
В фильме «Казино Рояль» в финальной раздаче покерного турнира у четырёх игроков оказываются следующие комбинации карт:
- Румянец
- Аншлаг
- Фулл-хаус (другой стоимости, чем первый)
- Прямой смыв
Какова вероятность этого?
Для этого мне пришлось провести симуляцию. В моей симуляции я предполагаю, что никто никогда не сбрасывает карты. При проведении почти 2,2 миллиарда раундов это произошло 312 раз. Это соответствует вероятности примерно 1 к семи миллионам.


