На этой странице
Система ставок Oscar's Grind
Введение
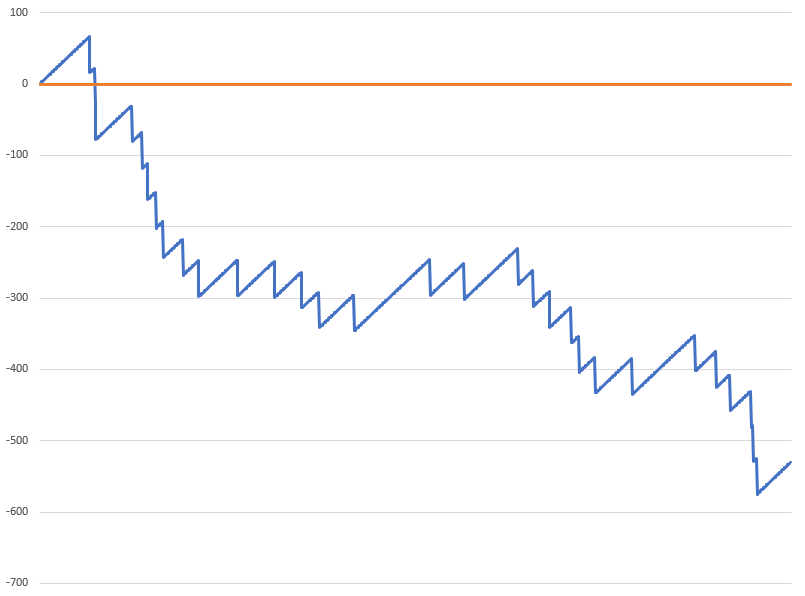
Система ставок «Scar's Grind» — популярная система ставок. В основном, в ней используются ставки с равными шансами и заданной целью выигрыша. Как и большинство систем ставок, она обычно достигает этой цели, но при этом приводит к большим убыткам, если этого не происходит. Как и любая система ставок, она не выдерживает испытания временем и в конечном итоге покажет чистый убыток.
В отличие от большинства систем ставок, таких как Мартингейл, Лабушер или Фибоначчи , игрок увеличивает ставку после выигрыша, а не после проигрыша. Кроме того, размер ставки не увеличивается так быстро, как в этих системах, что делает достижение выигрышной цели более «тяжелым» процессом. Это снижает шансы на выигрыш по сравнению с более агрессивными системами, но также позволяет игроку играть дольше и с меньшей средней ставкой.
В целом, Oscar's Grind, как правило, выигрывает в нестабильных играх и показывает плохие результаты в играх с переменным успехом.
Правила
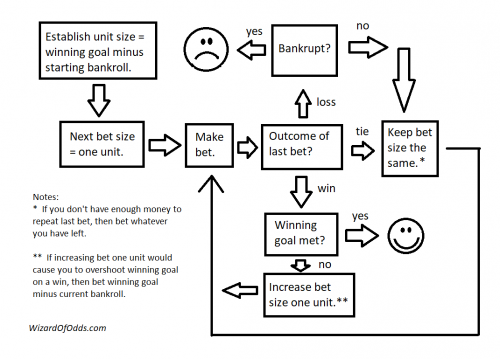
Ниже описано, как играть в Oscar's Grind на ставках с равными шансами.
- Игрок выберет победный гол и пополнит свой игровой баланс.
- Ставка в одну единицу должна быть равна выигрышному голу.
- Игрок делает ставку в одну единицу.
- Если игрок проигрывает или играет вничью, он повторяет ту же ставку*.
- Если игрок выигрывает, то увеличивает свою следующую ставку на одну единицу**.
- Игрок продолжает повторять это до тех пор, пока либо не достигнет своей выигрышной цели, либо не проиграет весь свой банкролл.
Примечания:
*: Если у игрока недостаточно денег, чтобы повторить ту же ставку, он ставит столько, сколько может.
**: Если выигрыш следующей ставки приведет к тому, что игрок превысит свой выигрышный лимит, то он уменьшает свою ставку до выигрышного лимита за вычетом текущего баланса.
Вот моя блок-схема игры. Начните с верхнего левого квадрата. Нажмите на изображение для увеличения.
Результаты моделирования
Чтобы показать, чего ожидать от использования Oscar's Grind, я написал симуляцию, которая следовала вышеуказанным правилам, основанным на различных ставках и играх. В симуляции использовался генератор случайных чисел Mersenne Twister. Для каждой симуляции целевой выигрыш составлял десять единиц. Я протестировал симуляцию на следующих суммах: 10, 25, 50, 100, 250 и 500 единиц.
Первая симуляция основана на ставках игрока в баккара . Размер симуляции составляет более 37 миллиардов сессий. Напомним, что теоретическое преимущество казино на ставке игрока составляет 1,235%.
Симуляция баккара — Ставка игрока
| Статистика | 10 единиц | 25 единиц | 50 единиц | 100 единиц | 250 единиц |
|---|---|---|---|---|---|
| Вероятность достижения победного гола высока. | 90,17% | 95,65% | 97,69% | 98,77% | 99,46% |
| Среднее количество ставок | 4.736 | 5.697 | 6.230 | 6.646 | 7.067 |
| Средняя сумма ставки | 6.626 | 10.609 | 14.557 | 19.609 | 28.650 |
| Ожидаемый выигрыш за сессию | -0.082 | -0.131 | -0.180 | -0.242 | -0.354 |
| Соотношение проигранных денег к сумме ставки | 1,234% | 1,235% | 1,236% | 1,235% | 1,235% |
Первая симуляция основана на ставке на «пас» в крэпсе . Размер симуляции составляет более 45 миллиардов сессий. Напомним, что теоретическое преимущество казино на ставке на «пас» составляет 1,41%.
Симулятор игры в кости — Ставка Pass
| Статистика | 10 единиц | 25 единиц | 50 единиц | 100 единиц | 250 единиц |
|---|---|---|---|---|---|
| Вероятность достижения победного гола высока. | 90,14% | 95,63% | 97,67% | 98,76% | 99,45% |
| Среднее количество ставок | 4.289 | 5.161 | 5.645 | 6.024 | 6.409 |
| Средняя сумма ставки | 6.001 | 9.616 | 13.205 | 17.804 | 26.051 |
| Ожидаемый выигрыш за сессию | -0.085 | -0.136 | -0.187 | -0.252 | -0.368 |
| Соотношение проигранных денег к сумме ставки | 1,413% | 1,414% | 1,414% | 1,414% | 1,413% |
Следующая симуляция основана на ставке «не проходит» в крэпсе . Размер симуляции составил более 43 миллиардов сессий. Напомним, что преимущество казино на ставке «не проходит» составляет 1,364%.
Симулятор игры в кости — Не пройди
| Статистика | 10 единиц | 25 единиц | 50 единиц | 100 единиц | 250 единиц |
|---|---|---|---|---|---|
| Вероятность достижения победного гола высока. | 90,14% | 95,64% | 97,68% | 98,76% | 99,46% |
| Среднее количество ставок | 4.410 | 5.307 | 5.805 | 6.193 | 6.589 |
| Средняя сумма ставки | 6.171 | 9.887 | 13.574 | 18.296 | 26.768 |
| Ожидаемый выигрыш за сессию | -0.084 | -0.135 | -0.185 | -0.250 | -0.365 |
| Соотношение проигранных денег к сумме ставки | 1,364% | 1,364% | 1,364% | 1,364% | 1,364% |
Следующая симуляция основана на любой ставке с равными шансами в рулетке с одним нулем. Размер симуляции составил более 43 миллиардов сессий. Напомним, что теоретическое преимущество казино составляет 1/37 = 2,703%.
Имитация рулетки — с одним нулем
| Статистика | 10 единиц | 25 единиц | 50 единиц | 100 единиц | 250 единиц |
|---|---|---|---|---|---|
| Вероятность достижения победного гола высока. | 89,40% | 95,11% | 97,29% | 98,49% | 99,28% |
| Среднее количество ставок | 4.381 | 5.327 | 5.871 | 6.314 | 6.789 |
| Средняя сумма ставки | 6.156 | 10.059 | 14.074 | 19.418 | 29.545 |
| Ожидаемый выигрыш за сессию | -0.166 | -0.272 | -0.380 | -0.525 | -0.799 |
| Соотношение проигранных денег к сумме ставки | 2,703% | 2,702% | 2,703% | 2,702% | 2,703% |
Следующая симуляция основана на любой ставке с равными шансами в рулетке с двойным нулем. Размер симуляции составил более 45 миллиардов сессий. Напомним, что теоретическое преимущество казино составляет 2/38 = 5,263%.
Имитация рулетки — Двойной ноль
| Статистика | 10 единиц | 25 единиц | 50 единиц | 100 единиц | 250 единиц |
|---|---|---|---|---|---|
| Вероятность достижения победного гола высока. | 87,81% | 93,93% | 96,39% | 97,81% | 98,81% |
| Среднее количество ставок | 4.567 | 5.670 | 6.350 | 6.944 | 7.646 |
| Средняя сумма ставки | 6.468 | 10.982 | 15.945 | 23.026 | 37.824 |
| Ожидаемый выигрыш за сессию | -0.340 | -0.578 | -0.839 | -1.212 | -1.991 |
| Соотношение проигранных денег к сумме ставки | 5,263% | 5,264% | 5,262% | 5,264% | 5,264% |
Видео
Вот моё видео об Оскаре и его стиле игры.
Внутренние ссылки
- Система ставок Лабушера .
- Система ставок Фибоначчи .
- Система ставок Мартингейла .
- Система ставок «Анти-Мартингейл» .
- Система ставок Д'Аламбера .
- Система рулетки Кифера .
Внешние ссылки
Обсуждение игры Oscar's Grind на моём форуме в Wizard of Vegas.