На этой странице
Вероятности выигрыша в бинго: анализ прогрессивного джекпота Jumbo в казино Station.
На этой странице
Обновлять
С момента написания моего первого отчета, в казино Station, по всей видимости, снова изменилось распределение четных и нечетных чисел, вероятно, где-то в октябре. В следующей таблице показано недавнее распределение карт, взятых мной и другим игроком, которого я назову «L».
 Огайо Рекомендуемые онлайн-комнаты для игры в бинго
Огайо Рекомендуемые онлайн-комнаты для игры в бинго
Новые образцы больших бинго-карточек
| Число шансов | Образец Майка | Образец Л. | Общая выборка | Вероятность |
|---|---|---|---|---|
| 9 | 2 | 3 | 5 | 0.011261 |
| 10 | 7 | 10 | 17 | 0.038288 |
| 11 | 14 | 25 | 39 | 0.087838 |
| 12 | 34 | 41 | 75 | 0.168919 |
| 13 | 41 | 71 | 112 | 0.252252 |
| 14 | 86 | 110 | 196 | 0.441441 |
| Общий | 184 | 260 | 444 | 1 |
Хотя диапазон шансов от 9 до 14 остается прежним, вероятность теперь значительно смещена в сторону 14, в отличие от более равномерного распределения ранее. Большие шансы затрудняют выигрыш прогрессивного джекпота. На основе этой выборки я теперь рекомендую ждать, пока значение большого шара не достигнет 54, если вы хотите получить положительное ожидаемое значение.
В следующей таблице сравниваются мои общие результаты выборки с ожидаемыми суммами при том же размере выборки и вероятности каждой суммы, если предположить тот же метод розыгрыша карт, который мне ранее объяснил Стивен Л. Кавалларо (исполнительный вице-президент и главный операционный директор Station Casinos).
Фактические и ожидаемые итоговые показатели
| Число шансов | Сумма выборки | Ожидаемая сумма |
|---|---|---|
| 9 | 5 | 33.17 |
| 10 | 17 | 60.48 |
| 11 | 39 | 87.61 |
| 12 | 75 | 101.15 |
| 13 | 112 | 93.18 |
| 14 | 196 | 68.41 |
| Общий | 444 | 444 |
Совершенно очевидно, что мои результаты не соответствуют ожиданиям. Статистический тест на асимметрию этого распределения по сравнению с ожиданиями дает значение хи-квадрат, равное 330,71 при 5 степенях свободы. Вероятность получения результатов с такой или большей асимметрией составляет 1 к 402 433 741 048 496 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000. Для сравнения, вероятность выигрыша в лотерею Powerball восемь раз подряд выше.
В качестве дополнительного аргумента в пользу изменения способа розыгрыша карт, в следующей таблице представлены результаты моей выборки до и после предполагаемого изменения. Выборка 1 была взята в августе, выборка 2 — 30 октября и 1 ноября.
Старый против нового образца
| Число шансов | Образец 1 | Образец 2 | Пример 1 Вероятность | Вероятность образца 2 |
|---|---|---|---|---|
| 9 | 35 | 5 | 13,51% | 1,13% |
| 10 | 35 | 17 | 13,51% | 3,83% |
| 11 | 34 | 39 | 13,13% | 8,78% |
| 12 | 48 | 75 | 18,53% | 16,89% |
| 13 | 55 | 112 | 21,24% | 25,23% |
| 14 | 52 | 196 | 20,08% | 44,14% |
| Общий | 259 | 444 | 100% | 100% |
На следующем графике сравниваются два столбца вероятностей в приведенной выше таблице относительно ожидаемых вероятностей.
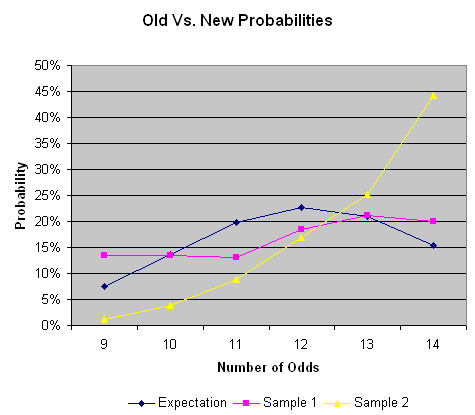
Я направил запрос руководству Station Casinos по поводу процедуры розыгрыша новых карт, и мне ответили, что никаких изменений в процедуре не произошло. Мои показания, опровергающие это, никак не были прокомментированы, и из-за моего «негативного сообщения» мне было отказано в дальнейшем сотрудничестве.
Примечания: Образец Майка был собран в 15:00 1 ноября на станции Сансет. Образец Л. был собран в 9:00 и 11:00 30 октября на станции Боулдер.
Ниже приведено мое первоначальное исследование, которое сейчас устарело.
Ниже приведены мои доказательства того, что прогрессивные бинго-карты, продаваемые в следующих казино Лас-Вегаса, создаются не совсем случайным образом.
- Станция "Палас"
- Станция Санта-Фе
- Техасская станция
- Станция Боулдер
- Станция Сансет
- Фиеста Ранчо
- Фиеста Хендерсон
- Город Сэма
В казино Station в Лас-Вегасе действует прогрессивный джекпот в бинго под названием Jumbo Bingo. Начальный прогрессивный джекпот составляет 100 000 долларов. Для выигрыша игрок должен собрать все 24 числа на карточке (так называемый Jumbo Ball) за 47 ходов. Если ни в одном из пяти бинго-залов в первую неделю никто не соберет джекпот, количество ходов для выигрыша прогрессивного джекпота (называемого Jumbo Ball) увеличивается на один до 48. Аналогично, Jumbo Ball будет увеличиваться на один каждую неделю, пока кто-нибудь не выиграет.
Очевидно, чтобы сэкономить время, первые 37 названных чисел — это четные числа от 2 до 74. На больших карточках бинго удобно отмечены все четные числа. В начале игры ведущий спросит, выиграл ли кто-нибудь, имея на карточке все четные числа. Затем, после того как никто не заявит о выигрышной карточке, ведущий будет случайным образом вытягивать шары, игнорируя шары с четными номерами. Если никто не соберет все выигрышные числа к моменту объявления большого шара, предусмотрен утешительный приз в размере 5000 долларов за все выигрышные числа в течение 52 вызовов. Если никто не заявит о выигрыше, предусмотрен приз в размере 1199 долларов для первого игрока, собравшего все выигрышные числа, независимо от количества вызовов. Как всегда в бинго, любой приз делится, если несколько игроков выигрывают одновременно.
В казино Fiesta есть очень похожая игра, но в меньшем масштабе. Прогрессивный джекпот начинается с 25 000 долларов, а утешительные призы меньше. Суть в том, что все четные числа объявляются заранее. В Sam's Town игра обратная: нечетные числа объявляются заранее.
В следующей таблице показано распределение вероятностей в зависимости от общего количества нечетных чисел на карте для честной карты. Мое определение честной карты — это карта, в которой 5 чисел «B» выбираются случайным образом из чисел от 1 до 15, 5 чисел «I» выбираются случайным образом из чисел от 16 до 30 и так далее. Другой способ добиться того же результата — это вытягивать числа от 1 до 75, заполняя карту по мере выбора чисел, и игнорировать числа, если соответствующий столбец уже заполнен.
Вероятность выпадения нечетного числа в сумме - честная карта
| Число шансов | Вероятность | Обратная вероятность |
|---|---|---|
| 0 | 0.000000000436 | 1 из 2293355030 |
| 1 | 0.000000022747 | 1 из 43962077 |
| 2 | 0.000000534794 | 1 из 1869877 |
| 3 | 0.000007530006 | 1 из 132802 |
| 4 | 0.000071202834 | 1 из 14044 |
| 5 | 0.000480801205 | 1 в 2080 году |
| 6 | 0.002407676276 | 1 из 415 |
| 7 | 0.00916827051 | 1 из 109 |
| 8 | 0.027013789916 | 1 из 37 |
| 9 | 0.062346657338 | 1 из 16 |
| 10 | 0.113677702037 | 1 из 9 |
| 11 | 0.164671200005 | 1 из 6 |
| 12 | 0.1901222602 | 1 из 5 |
| 13 | 0.175132872532 | 1 из 6 |
| 14 | 0.1285740634 | 1 из 8 |
| 15 | 0.074984221403 | 1 из 13 |
| 16 | 0.034540809008 | 1 из 29 |
| 17 | 0.012458867878 | 1 из 80 |
| 18 | 0.003475365511 | 1 из 288 |
| 19 | 0.00073657509 | 1 из 1358 |
| 20 | 0.000115624911 | 1 из 8649 |
| 21 | 0.000012937867 | 1 из 77292 |
| 22 | 0.000000969822 | 1 из 1031117 |
| 23 | 0.000000043401 | 1 из 23041075 |
| 24 | 0.000000000872 | 1 из 1146677515 |
| Общий | 1 | 1 из 1 |
Очевидно, что карточка с очень небольшим количеством нечетных чисел будет иметь хороший старт и гораздо больше шансов на выигрыш, чем карточка с преимущественно нечетными числами. В июльском номере журнала Las Vegas Advisor за 2002 год я написал статью о гигантском бинго, основываясь на предположении, что карточки создавались случайным образом. Один из читателей этой колонки сказал мне, что, по его мнению, карточки не создавались случайным образом, о чем свидетельствует тот факт, что он купил 1500 карточек, и на всех них суммарное количество нечетных чисел находилось в диапазоне от 9 до 14.
Чтобы подтвердить утверждение о том, что на всех карточках вероятность выпадения чисел составляла от 9 до 14, мой помощник Роб Фельдхайм собрал 259 больших карточек для бинго на вокзале «Палас». Затем мы подсчитали количество вероятностей на каждой карточке, и, как я и опасался, общее количество вероятностей всегда составляло от 9 до 14. В следующей таблице показано общее количество вероятностей для каждого числа и ожидаемое общее количество в честной игре.
Карты Palace Station: фактическое значение против ожидаемого
| Число шансов | Число в образце | Ожидал Общий |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000006 |
| 2 | 0 | 0.000139 |
| 3 | 0 | 0,00195 |
| 4 | 0 | 0.018442 |
| 5 | 0 | 0.124528 |
| 6 | 0 | 0.623588 |
| 7 | 0 | 2.374582 |
| 8 | 0 | 6.996572 |
| 9 | 35 | 16.147784 |
| 10 | 35 | 29.442525 |
| 11 | 34 | 42.649841 |
| 12 | 48 | 49.241665 |
| 13 | 55 | 45.359414 |
| 14 | 52 | 33.300682 |
| 15 | 0 | 19.420913 |
| 16 | 0 | 8.94607 |
| 17 | 0 | 3.226847 |
| 18 | 0 | 0.90012 |
| 19 | 0 | 0.190773 |
| 20 | 0 | 0.029947 |
| 21 | 0 | 0.003351 |
| 22 | 0 | 0.000251 |
| 23 | 0 | 0.000011 |
| 24 | 0 | 0 |
| Общий | 259 | 259 |
Вероятность того, что общее количество шансов окажется в диапазоне от 9 до 14, составляет 0,834524756. Из выборки в 42,858088 чисел должно было оказаться за пределами диапазона от 9 до 14, но вместо этого ни одно из них не оказалось за его пределами. Вероятность такого события в честной игре составляет 0,834524756 259 = 4,4953 * 10 -21 , или 1 из 222 454 364 282 805 000 000.
Вот результаты аналогичного теста, проведенного на карточках бинго Grande, полученных после сеанса в 11:00 утра 22 августа 2002 года в Fiesta Rancho.
Результаты розыгрыша карточек Fiesta Rancho: фактические и ожидаемые
| Число шансов | Число в образце | Ожидал Общий |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000002 |
| 2 | 0 | 0.000047 |
| 3 | 0 | 0.000655 |
| 4 | 0 | 0.006195 |
| 5 | 0 | 0.04183 |
| 6 | 0 | 0.209468 |
| 7 | 0 | 0.79764 |
| 8 | 0 | 2.3502 |
| 9 | 10 | 5.424159 |
| 10 | 6 | 9.88996 |
| 11 | 19 | 14.326394 |
| 12 | 18 | 16.540637 |
| 13 | 18 | 15.23656 |
| 14 | 16 | 11.185944 |
| 15 | 0 | 6.523627 |
| 16 | 0 | 3.00505 |
| 17 | 0 | 1.083922 |
| 18 | 0 | 0.302357 |
| 19 | 0 | 0.064082 |
| 20 | 0 | 0.010059 |
| 21 | 0 | 0.001126 |
| 22 | 0 | 0.000084 |
| 23 | 0 | 0.000004 |
| 24 | 0 | 0 |
| Общий | 87 | 87 |
Далее представлены результаты тестирования мною нескольких прогрессивных джекпотов от Sams Town.
Карты Sam's Town: фактическое соотношение с ожидаемым
| Число из Эвенов | Число в образце | Ожидал Общий |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000002 |
| 2 | 0 | 0.000055 |
| 3 | 0 | 0.000768 |
| 4 | 0 | 0.007263 |
| 5 | 0 | 0.049042 |
| 6 | 0 | 0.245583 |
| 7 | 0 | 0.935164 |
| 8 | 1 | 2.755407 |
| 9 | 1 | 6.359359 |
| 10 | 19 | 11.595126 |
| 11 | 25 | 16.796462 |
| 12 | 24 | 19.392471 |
| 13 | 20 | 17.863553 |
| 14 | 12 | 13.114554 |
| 15 | 0 | 7.648391 |
| 16 | 0 | 3.523163 |
| 17 | 0 | 1.270805 |
| 18 | 0 | 0.354487 |
| 19 | 0 | 0.075131 |
| 20 | 0 | 0.011794 |
| 21 | 0 | 0,00132 |
| 22 | 0 | 0.000099 |
| 23 | 0 | 0.000004 |
| 24 | 0 | 0 |
| Общий | 102 | 102 |
Я ожидал получить в Sam's Town комбинацию из 10-15 четных чисел или 9-14 четных, основываясь на разговоре со Стивеном Л. Кавалларо из Station Casinos. Однако мне выпала одна карта с 8 четными числами, и только одна с 9. Вероятность того, что любая карта будет иметь от 8 до 14 четных чисел, составляет 0,881703. Вероятность того, что 102 карты попадут в этот диапазон, составляет 2,647786 * 10⁻⁶ , или 1 из 377 674.
Кроме того, я провел аналогичный тест на обычных бинго-карточках из Санкоста. Выборка из 129 карточек показала следующие фактические и ожидаемые результаты.
Карты Suncoast: фактическое соотношение с ожидаемым
| Число шансов | Число в образце | Ожидал Общий |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0.000003 |
| 2 | 0 | 0.000069 |
| 3 | 0 | 0.000971 |
| 4 | 0 | 0.009185 |
| 5 | 0 | 0.062023 |
| 6 | 0 | 0.31059 |
| 7 | 1 | 1.182707 |
| 8 | 6 | 3.484779 |
| 9 | 5 | 8.042719 |
| 10 | 17 | 14.664424 |
| 11 | 19 | 21.242585 |
| 12 | 29 | 24.525772 |
| 13 | 20 | 22.592141 |
| 14 | 18 | 16.586054 |
| 15 | 10 | 9.672965 |
| 16 | 1 | 4.455764 |
| 17 | 3 | 1.607194 |
| 18 | 2 | 0.448322 |
| 19 | 0 | 0.095018 |
| 20 | 0 | 0.014916 |
| 21 | 0 | 0.001669 |
| 22 | 0 | 0,000125 |
| 23 | 0 | 0.000006 |
| 24 | 0 | 0 |
| Общий | 129 | 129 |
Из 129 карт 21 вышло за пределы диапазона от 9 до 14, ожидаемое число составляло 21,34630654. Эти карты легко прошли проверку на четность/нечетность. Так и должно было быть, поскольку не было игры, в которой четные или нечетные числа объявлялись заранее.
В следующей таблице показана вероятность выигрыша в честной игре при условии, что игрок должен собрать все числа, находящиеся в пределах 50.
Вероятность выигрыша - Честная карта
| Число шансов | Вероятность карты | Вероятность Карточные выигрыши | Общий Вероятность |
|---|---|---|---|
| 0 | 0.000000000436 | 1 | 0.000000000436 |
| 1 | 0.000000022747 | 0.342105263158 | 0.000000007782 |
| 2 | 0.000000534794 | 0.110953058321 | 0.000000059337 |
| 3 | 0.000007530006 | 0.033902323376 | 0.000000255285 |
| 4 | 0.000071202834 | 0.009686378107 | 0.000000689698 |
| 5 | 0.000480801205 | 0.002564041264 | 0.000001232794 |
| 6 | 0.002407676276 | 0.000621585761 | 0.000001496577 |
| 7 | 0.00916827051 | 0.000135971885 | 0.000001246627 |
| 8 | 0.027013789916 | 0.000026317139 | 0.000000710926 |
| 9 | 0.062346657338 | 0.00000438619 | 0.000000273464 |
| 10 | 0.113677702037 | 0.000000604992 | 0.000000068774 |
| 11 | 0.164671200005 | 0.000000064821 | 0.000000010674 |
| 12 | 0.1901222602 | 0.000000004802 | 0.000000000913 |
| 13 | 0.175132872532 | 0.000000000185 | 0.000000000032 |
| 14 | 0.1285740634 | 0 | 0 |
| 15 | 0.074984221403 | 0 | 0 |
| 16 | 0.034540809008 | 0 | 0 |
| 17 | 0.012458867878 | 0 | 0 |
| 18 | 0.003475365511 | 0 | 0 |
| 19 | 0.00073657509 | 0 | 0 |
| 20 | 0.000115624911 | 0 | 0 |
| 21 | 0.000012937867 | 0 | 0 |
| 22 | 0.000000969822 | 0 | 0 |
| 23 | 0.000000043401 | 0 | 0 |
| 24 | 0.000000000872 | 0 | 0 |
| Общий | 1 | 0 | 0.000006053319 |
На нижнем изображении справа показана общая вероятность выигрыша, равная 0,000006053319, или 1 к 165199. Если в честной игре происходит выигрыш, обратите внимание, что он наиболее вероятен при выпадении карты с вероятностью 6. Вероятность того, что выигрышная карта в честной игре будет иметь вероятность менее 9, составляет 94,15%.
Когда стало известно о моих планах написать о своем расследовании, меня попросили встретиться со Стивеном Л. Кавалларо (исполнительным вице-президентом и главным операционным директором Station Casinos) и Джонатаном Суэйном (вице-президентом и генеральным менеджером Palace Station). Стивен сразу же признал, что карты были заранее отобраны таким образом, чтобы каждая содержала от 9 до 14 шансов. Он сказал, что это было сделано для того, чтобы уравнять шансы и дать каждой карте и каждому клиенту надежду на победу. Он также сказал, что изначально диапазон был намного шире, и что у первого победителя изначально было всего 3 шанса на карте. Кроме того, он сказал, что Sam's Town и Fiesta Casinos делают то же самое, и что игра в Station полностью одобрена Советом по контролю за азартными играми штата Невада.
В последующем телефонном разговоре Стивен Кавалларо рассказал мне, что карты создаются следующим образом: компьютер случайным образом выбирает набор честных чисел. Если сумма чисел находится в диапазоне от 9 до 14, карта печатается, в противном случае этот набор чисел отбрасывается, и начинается следующий. В следующей таблице показана скорректированная вероятность каждого числа при таком способе создания карт.
Вероятность выпадения нечетного числа чисел на карточке станции
| Количество шансов | Вероятность |
|---|---|
| 9 | 0.074709 |
| 10 | 0.136218 |
| 11 | 0.197323 |
| 12 | 0.227821 |
| 13 | 0.209859 |
| 14 | 0.154069 |
| Общий | 1 |
В целом, удаление лучших карт из комбинации приводит к тому, что вероятность выигрыша прогрессивного джекпота с любой конкретной картой существенно снижается. Удаление худших карт не компенсирует этого. Такая политика предварительного отбора карт приводит к увеличению джекпотов. В то же время казино приходится реже пополнять счетчик. В результате уменьшается количество победителей прогрессивного джекпота и общая сумма выигранных призовых денег. В следующей таблице показана ожидаемая вероятность выигрыша как честной карты, так и карты «Станции» в зависимости от количества шаров, выпавших для выигрыша джекпота.
Ожидаемая вероятность выигрыша
| Число звонков | Справедливая карта | Карта станций | Соотношение |
|---|---|---|---|
| 47 | 1 из 1 122 373 | 1 из 205 287 873 | 182.91 |
| 48 | 1 из 583 217 | 1 из 35 037 983 | 60.08 |
| 49 | 1 из 308 005 | 1 из 8 203 638 | 26.63 |
| 50 | 1 из 165 199 | 1 из 2 358 363 | 14.28 |
| 51 | 1 из 89 925 | 1 из 785 008 | 8.73 |
| 52 | 1 из 49 648 | 1 из 291 923 | 5.88 |
| 53 | 1 из 27 784 | 1 из 118 433 | 4.26 |
В столбце «Соотношение» показано, во сколько раз сложнее выиграть, используя карту казино Station, по сравнению с обычной картой. Например, выиграть в 14,28 раза сложнее, если джекпот нужно выиграть, выпав за 50 или менее шаров.
Я считаю, что все карточки для бинго должны создаваться абсолютно случайным образом, как предложено выше. В противном случае, я полагаю, что если карточка не создается случайным образом, правила должны быть раскрыты относительно способа ее создания и влияния на игрока. Во всех видах азартных игр я решительно поддерживаю честность и прозрачность. Ни то, ни другое, на мой взгляд, не соблюдается в бинго в штате Невада. Поэтому пусть игроки в бинго будут осторожны.
Я благодарю Стивена Кавалларо и Джонатана Суэйма за встречу со мной и за их откровенность в этом вопросе.
Вернуться к вероятностям в бинго Майкл Шеклфорд, ASA
 Огайо Рекомендуемые онлайн-казино
Огайо Рекомендуемые онлайн-казино
Посмотреть все
Бонус до $11 000
Приглашаются все игроки из США.
Более 200 игр в казино.
Играйте на ПК или мобильном устройстве
Бонус до $3000
Казино и букмекерская контора
Только для американских игроков
Играйте на компьютере или мобильном устройстве.
7777 долларов + 300 бесплатных вращений
Игры с живыми дилерами
Ежедневные бесплатные турниры
Удобно для мобильных и настольных устройств.
Другие страницы бинго
- Моя общая страница бинго
- Джекпоты Cash Ball на станции Palace Station за 2007 год .
- Джекпоты Cash Ball в Боулдер-Стейшн за 2007 год
- Джекпоты Fiesta Henderson Cash Ball на 2007 год
- Джекпоты Cash Ball на станции Texas Station за 2007 год
- Джекпоты Cash Ball на станции Sunset Station за 2007 год
- Джекпоты Cash Ball на станции Санта-Фе за 2007 год
- Джекпоты Red Rock Cash Ball за 2007 год
- Джекпоты Cash Ball от Coast Casinos за 2007 год






