На этой странице
Бонусный крэпс
Введение
Бонусная ставка в крэпсе — это набор из трех дополнительных ставок, встречающихся в игре в крэпс. Вот некоторые из них:
- Небольшая ставка — выигрыш, если игрок выбросит все числа от 2 до 6, прежде чем сумма выпадет 7. Обычно выигрыш выплачивается в соотношении 30 к 1.
- «Высокий» — выигрывает, если игрок выбросит все числа от 8 до 12, прежде чем сумма выпадет 7. Выигрыш обычно составляет 30 к 1.
- Все — выигрывает, если игрок выбросит все числа от 2 до 12, кроме 7, прежде чем сумма выпадет 7. Выигрыш обычно выплачивается в соотношении 150 к 1.
В 2021 году я начал замечать подобные ставки, называемые "Дайсология", в отеле Venetian.
Анализ
В следующей таблице представлен мой анализ ставок «Малый» и «Большой», где выигрыши выплачиваются в соотношении 30 к 1. В нижней правой ячейке показано преимущество казино в 18,30%.
Маленький и высокий
| Событие | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| Победить | 30 | 0.026354 | 0.790617 |
| Потеря | -1 | 0.973646 | -0.973646 |
| Общий | 1.000000 | -0.183029 |
В прошлом за некоторыми столами выплачивались выигрыши 34 к 1 на карты Small и Tall. При таких более щедрых шансах преимущество казино составляет 7,76%.
В следующей таблице представлен мой анализ ставки «Все», когда выигрыш выплачивается в соотношении 150 к 1. В нижней правой ячейке показано преимущество казино в 20,61%.
Все
| Событие | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| Победить | 150 | 0.005258 | 0.788655 |
| Потеря | -1 | 0.994742 | -0.994742 |
| Общий | 1.000000 | -0.206087 |
Я видел и другие выплаты по ставке «Все», включая 155 и 175 к 1. Не забудьте вычесть единицу из выплаты, чтобы перевести коэффициенты «за одного» в коэффициенты «за одного». В следующей таблице показано преимущество казино для всех выплат, делящихся на 5, от 150 до 175.
Краткий обзор преимущества казино по всем ставкам
| Платит | Край дома |
|---|---|
| 150 | 20,61% |
| 155 | 17,98% |
| 160 | 15,35% |
| 165 | 12,72% |
| 170 | 10,09% |
| 175 | 7,46% |
Методология
Я проанализировал игру Bonus Craps тремя способами, а именно:
- Моделирование — это, пожалуй, самый простой способ. Однако для таких математических пуристов, как я, моделирование всегда оказывается интеллектуально неудовлетворительным.
- Цепь Маркова — этот метод утомителен и занимает много времени. Для малых и высоких значений потребуется матрица переходов 6x6, а для всех — 12x12.
- Интегральное исчисление — этот метод удивительно прост при использовании калькулятора интегралов. Ниже я объясню его подробнее.
Представьте, что вместо того, чтобы значимые события определялись броском игральных костей по одному, рассматривайте их как мгновение во времени. Предположим, что время между событиями обладает свойством отсутствия памяти, со средним временем между событиями в одну единицу времени. Другими словами, время между событиями подчиняется экспоненциальному распределению со средним значением 1. Это не будет иметь значения для целей разрешения пари, поскольку события по-прежнему происходят по одному.
Ниже приведена вероятность того, что любая заданная сумма чисел НЕ выпадала хотя бы один раз в течение x единиц времени:
- 2 или 12: exp(-x/36)
- 3 или 11: exp(-x/18)
- 4 или 10: exp(-x/12)
- 5 или 9: exp(-x/9)
- 6 или 8: exp(-5x/36)
- 7: exp(-x/6)
Давайте сначала рассмотрим небольшую ставку. Коэффициенты для большой ставки точно такие же.
Вероятность того, что за x единиц времени выпали числа 2, 3, 4, 5 и 6, а число 7 не выпало, равна: (1-exp(-x/36))*(1-exp(-x/18))*(1-exp(-x/12))*(1-exp(-x/9))*(1-exp(-5x/36))*exp(-x/6). Вероятность того, что в момент времени x игрок выбросит 7, имея до этого все суммы от 2 до 6, равна:
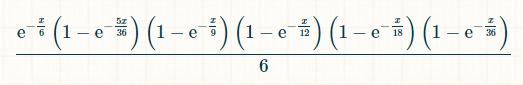
Для интегрирования я использовал этот калькулятор интегралов .
Поскольку выигрышная семерка может выпасть в любой момент времени, вероятность выигрыша равна интегралу этой вероятности по x от 0 до бесконечности. Нам это знать не обязательно, но интеграл, до подстановки пределов интегрирования, равен (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^(-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(- (7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^(-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
С учетом пределов интегрирования, ответ равен 20049 / 760760 = приблизительно 0,02635390924864609.
Далее рассмотрим ставку «Все».
Вероятность того, что за x единиц времени выпали числа 2, 3, 4, 5, 6, 8, 9, 10, 11 и 12, а число 7 не выпало, равна: (1-exp(-x/36)) 2 *(1-exp(-x/16)) 2 *(1-exp(-x/12)) 2 *(1-exp(-x/9)) 2 *(1-exp(-5x/36)) 2 *exp(-x/6). Вероятность того, что в момент времени x игрок выбросит 7, имея до этого все суммы от 2 до 6, равна:
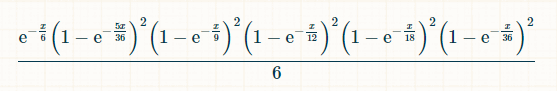
Поскольку выигрышная семерка может выпасть в любой момент времени, вероятность выигрыша — это интеграл этой вероятности по x от 0 до бесконечности. Нам это знать не нужно, но интеграл, до подстановки пределов интегрирования, равен (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1) 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6.
С учетом пределов интегрирования, ответ равен 126538525259 / 24067258815600 = 0,0052577040961964420049.



