На этой странице
Разные двойники
Введение
Ставка Different Doubles — это дополнительная ставка в крэпсе, которую можно встретить в казино Beau Rivage в Билокси. Выплата производится в зависимости от количества выпавших уникальных дублей, прежде чем сумма выпадет семь. Таблица выплат выглядит следующим образом:
- 6 парных ставок приносят выигрыш в соотношении 100 к 1.
- 5 парных ставок выплачиваются к 15.
- 4 дубля приносят выигрыш 8 к 1
- Три двойных ставки приносят выигрыш 4 к 1.
Анализ
В таблице ниже показана вероятность и вклад в доходность всех возможных исходов. В нижней правой ячейке указано преимущество казино в 27,92% (ой!).
Различные варианты возврата пар
| Парные удары сделаны | Платит | Комбинации | Вероятность | Возвращаться |
|---|---|---|---|---|
| 6 | 100 | 1 | 0.001082 | 0.108225 |
| 5 | 15 | 6 | 0.006494 | 0.097403 |
| 4 | 8 | 21 | 0.022727 | 0.181818 |
| 3 | 4 | 56 | 0.060606 | 0.242424 |
| 2 | -1 | 126 | 0.136364 | -0.136364 |
| 1 | -1 | 252 | 0.272727 | -0.272727 |
| 0 | -1 | 462 | 0.500000 | -0.500000 |
| Общий | 924 | 1.000000 | -0.279221 |
Алгебраический анализ
Вероятность выпадения любой двойной комбинации равна 1/36. Таким образом, вероятность ЛЮБОЙ двойной комбинации равна 6/36 = 1/6. Вероятность выпадения любой семерки равна 1/6. Мы можем игнорировать все броски, кроме двойных и семерок. Итак, если предположить, что был бросок, соответствующий ставке, ниже приведены вероятности для этого броска:
- Любая двойная ставка = 1/2
- Любая семерка = 1/2
Вероятность того, что первый значащий бросок выпадет семеркой, равна 1/2. Таким образом, вероятность выпадения двух одинаковых чисел равна нулю.
В противном случае игрок выбросил бы дубль. Теперь мы можем игнорировать повторное выпадение дубля как значимое событие. Вероятности обоих типов значимых событий теперь таковы:
- Любой значимый двойной удар = 5/11
- Любая семерка = 6/11
Вероятность того, что игрок выбросит семерку на этом этапе, то есть один дубль, составляет 6/11. Таким образом, общая вероятность одного дубля равна (1/2)*(6/11) = 3/11 = приблизительно 27,27%.
В противном случае игрок выбросил бы второй дубль. Теперь мы можем игнорировать выпадение двух разных дублей как значимое событие. Вероятности обоих типов значимых событий теперь таковы:
- Любое значимое удвоение = 4/10
- Любая семерка = 6/10
Вероятность того, что игрок выбросит семерку на этом этапе (два дубля), составляет 6/10. Таким образом, общая вероятность одного дубля равна (1/2)*(5/11)*(6/10) = 3/22 = приблизительно 13,6363636%.
В противном случае игрок выбросил бы третью дубль. Теперь мы можем игнорировать выпадение трех различных дублей как значимое событие. Вероятности обоих типов значимых событий теперь таковы:
- Любое значимое удвоение = 3/9
- Любая семерка = 6/9
Вероятность того, что игрок выбросит семерку на этом этапе (два дубля), составляет 6/9. Таким образом, общая вероятность одного дубля равна (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = приблизительно 6,060606%.
В противном случае игрок выбросил бы четвертую дубль. Теперь мы можем игнорировать выпадение четырех различных дублей как значимое событие. Вероятности обоих типов значимых событий теперь таковы:
- Любое значимое удвоение = 2/8
- Любая семерка = 6/8
Вероятность того, что игрок выбросит семерку на этом этапе (два дубля), составляет 6/8. Таким образом, общая вероятность одного дубля равна (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = приблизительно 2,272727%.
В противном случае игрок выбросил бы пятый дубль. Теперь мы можем игнорировать выпадение пяти различных дублей как значимое событие. Вероятности обоих типов значимых событий теперь таковы:
- Любое значимое удвоение = 1/7
- Любая семерка = 6/7
Вероятность того, что игрок выбросит семерку на этом этапе (два дубля), составляет 6/7. Таким образом, общая вероятность одного дубля равна (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = приблизительно 0,649351%.
В противном случае игрок выбросил бы последний оставшийся дубль. Вероятность этого составляет (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = приблизительно 0,108225%.
Теперь мы можем объединить все это в приведенной выше таблице результатов. Количество комбинаций составляет 924.
Анализ интегрального исчисления
Представьте, что вместо того, чтобы значимые события определялись броском игральных костей по одному, рассматривайте их как мгновение во времени. Предположим, что время между событиями обладает свойством отсутствия памяти, со средним временем между событиями в одну единицу времени. Другими словами, время между событиями подчиняется экспоненциальному распределению со средним значением 1. Это не будет иметь значения для целей разрешения пари, поскольку события все равно происходят по одному.
Время между конкретными удвоениями будет подчиняться экспоненциальному распределению со средним значением 12. Причина значения 12 заключается в том, что если происходит значимое событие, то вероятность того, что это было именно это конкретное удвоение, составляет 1/12. Таким образом, вероятность того, что конкретное удвоение не произошло за x единиц времени, равна exp(-x/12). Вероятность того, что оно произошло, равна 1-exp(-x/12).
Пусть x — количество единиц времени с момента начала ставки. Вероятность того, что выпало все два дубля, но не выпала семерка, равна (1-exp(-x/12)) 6 × exp(-x/2).
Чтобы завершить это выпадением семерки в момент времени x, умножьте это на 1/2, вероятность выпадения семерки, чтобы получить вероятность выигрыша ровно в момент времени x, равную (1/2) × (1-exp(-x/12)) 6 × exp(-x/2)
Чтобы найти вероятность выигрышной ставки за все время, проинтегрируйте от 1 до бесконечности:
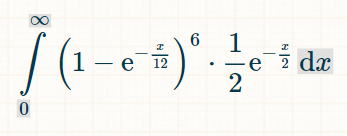
Для интегрирования я рекомендую этот калькулятор интегралов . В поле интеграла введите: "(1-exp(-x/12))^6*(1/2)*exp(-x/2)". В поле пределов интегрирования в параметрах укажите 0 и ∞. Затем нажмите "Перейти".Это позволит вам получить интеграл, приведенный ниже:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
Однако нам не нужно вводить 0. Калькулятор выдает ответ: 1/924 = приблизительно 0,001082251082251082.
Вот интеграл для пяти различных удвоений. Число 6 выбрано потому, что существует 6 возможных удвоений, которые не были созданы:
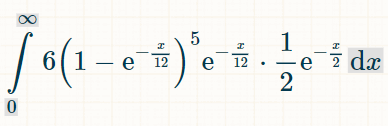
Вот вероятность выигрыша в течение x единиц времени:
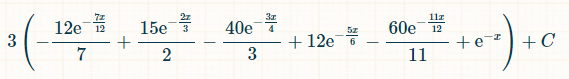
Если рассматривать вероятность выпадения ровно пяти различных дублей, то она составляет 1/154.
Вот интеграл для четырех различных удвоений. Число 15 объясняется тем, что существует 6!/(4!*2!) = 15 возможных комбинаций из 4 из 6 полученных удвоений:
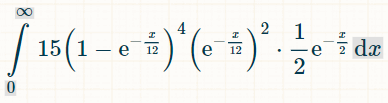
Вот вероятность выигрыша в течение x единиц времени:
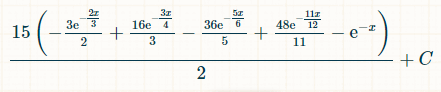
Если рассматривать вероятность выпадения ровно четырех различных дублей, то она составляет 1/44.
Вот интеграл для трех различных удвоений. Причина, по которой используется число 20, заключается в том, что существует 6!/(3!*3!) = 20 возможных комбинаций из 3 из 6 удвоений:
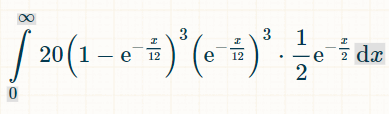
Вот вероятность выигрыша в течение x единиц времени:
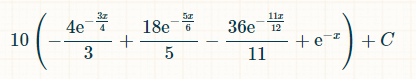
Если взять за основу интеграл от 0 до бесконечности, то вероятность выпадения ровно трех различных дублей составляет 2/33.



