На этой странице
Огненная ставка
Введение
Ставка «Огненная ставка» — популярная дополнительная ставка в крэпсе, выплата по которой зависит от количества уникальных очков, набранных и выигранных игроком. Мне известны три таблицы выплат, представленные ниже. Преимущество казино в каждой из них указано в нижней строке таблицы. Таблица выплат 1 является наиболее распространенной. Выплаты указываются «до единицы». Отрицательная единица означает проигрыш.
Таблицы выплат Fire Bet
| Высказанные тезисы | Таблица оплаты труда А | Таблица оплаты труда B | Таблица оплаты труда C |
|---|---|---|---|
| 6 | 999 | 2000 | 299 |
| 5 | 249 | 200 | 149 |
| 4 | 24 | 10 | 29 |
| 3 | -1 | -1 | 6 |
| 2 | -1 | -1 | -1 |
| 1 | -1 | -1 | -1 |
| 0 | -1 | -1 | -1 |
| Край дома | 20,76% | 24,86% | 20,73% |
Ниже приведён мой анализ таблицы выплат А. В нижней правой ячейке показана разница в 20,76% между игроками и букмекерской конторой.
Ставка «Огненная ставка» — Таблица выплат A
| Высказанные тезисы | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 24 | 0.008798 | 0.211156 |
| 5 | 249 | 0.001640 | 0.408343 |
| 6 | 999 | 0.000162 | 0.162272 |
| Общий | 1 | -0.207628 |
Ниже приведён мой анализ таблицы выплат B. В нижней правой ячейке показано преимущество казино в размере 24,86%.
Ставка «Огненная стихия» — Таблица выплат B
| Высказанные тезисы | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | -1 | 0.033434 | -0.033434 |
| 4 | 10 | 0.008798 | 0.087982 |
| 5 | 200 | 0.001640 | 0.327987 |
| 6 | 2000 | 0.000162 | 0.324869 |
| Общий | 1 | -0.248562 |
Ниже приведён мой анализ таблицы выплат C. В нижней правой ячейке показано преимущество казино в размере 20,73%.
Ставка «Огненная стихия» — Таблица выплат C
| Высказанные тезисы | Платит | Вероятность | Возвращаться |
|---|---|---|---|
| 0 | -1 | 0.593939 | -0.593939 |
| 1 | -1 | 0.260750 | -0.26075 |
| 2 | -1 | 0.101275 | -0.101275 |
| 3 | 6 | 0.033434 | 0.200605 |
| 4 | 29 | 0.008798 | 0.255147 |
| 5 | 149 | 0.001640 | 0.244350 |
| 6 | 299 | 0.000162 | 0.048568 |
| Общий | 1 | -0.207295 |
В следующей таблице показаны вероятности получения от 0 до 6 очков, с учетом максимально возможного количества значащих цифр, которое может обработать Excel.
Вероятности ставок на огонь
| Высказанные тезисы | Вероятность |
|---|---|
| 0 | 0.593939393939394 |
| 1 | 0.260750492003903 |
| 2 | 0.101275355549231 |
| 3 | 0.0334342121788456 |
| 4 | 0.00879817844040312 |
| 5 | 0.00163993313895325 |
| 6 | 0.000162434749269826 |
Меня часто спрашивают, как рассчитать вышеуказанные вероятности. Это непростая математическая задача. Ниже я перечислю три способа вычисления вероятности получения любого количества точек от 0 до 6.
Случайная симуляция
Случайная симуляция — самый простой способ анализа ставки Fire Bet. Благодаря скорости современных компьютеров она также чрезвычайно точна. Только самые строгие математики (вроде меня) будут стремиться к точному решению. В следующей таблице показаны результаты симуляции почти 40 миллиардов ставок Fire Bet, рассчитанных по таблице выплат A. В нижней правой ячейке показано преимущество казино в 20,7531%. Фактическое преимущество казино составляет 20,7628%, поэтому симуляция была точна с погрешностью в 0,01% от выигрыша.
Имитация ставок на пожар
| Высказанные тезисы | Платит | Победы | Вероятность | Возвращаться |
|---|---|---|---|---|
| 6 | 999 | 6 452 452 | 0.000162 | 0.162257 |
| 5 | 249 | 65,165,019 | 0.001640 | 0.408438 |
| 4 | 24 | 349,553,690 | 0.008799 | 0.211173 |
| 3 | -1 | 1 328 267 592 | 0.033435 | -0.033435 |
| 2 | -1 | 4 023 371 732 | 0.101275 | -0.101275 |
| 1 | -1 | 10,358,742,102 | 0.260747 | -0.260747 |
| 0 | -1 | 23,595,605,529 | 0.593941 | -0.593941 |
| Общий | 39,727,158,116 | 1.000000 | -0.207531 |
Цепь Маркова
Точный способ рассчитать вероятность выигрыша в «Огненной ставке» — использовать цепь Маркова. Это означает вычисление вероятности завершения любого будущего количества очков при любом из 64 возможных состояний уже завершенных очков. Математические вычисления довольно просты ближе к концу, нужно всего одно очко, чтобы завершить все шесть. Затем нужно вернуться к исходному состоянию первого броска.
Первое состояние представлено первой строкой таблицы, не считая заголовков столбцов. Оно показывает вероятности, указанные выше, для получения любого количества точек от 0 до 6.
Огненная ставка Цепь Маркова
| Баллы Уже Сделал | Вероятность 0 баллов | Вероятность 1 балл | Вероятность 2 балла | Вероятность 3 балла | Вероятность 4 балла | Вероятность 5 баллов | Вероятность 6 баллов |
|---|---|---|---|---|---|---|---|
| Никто | 0.593939 | 0.260750 | 0.101275 | 0.033434 | 0.008798 | 0.001640 | 0.000162 |
| 10 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 9 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 9,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 8 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 8,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 8,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6 | 0.000000 | 0.656067 | 0.244255 | 0.076831 | 0.019163 | 0.003370 | 0.000314 |
| 6,10 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 6,9 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 6,8 | 0.000000 | 0.000000 | 0.732710 | 0.210728 | 0.048135 | 0.007762 | 0.000665 |
| 6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5 | 0.000000 | 0.636364 | 0.252138 | 0.084540 | 0.022402 | 0.004153 | 0.000404 |
| 5,10 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 5,9 | 0.000000 | 0.000000 | 0.685315 | 0.237358 | 0.064328 | 0.011875 | 0.001124 |
| 5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 5,8 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6 | 0.000000 | 0.000000 | 0.708220 | 0.225365 | 0.055933 | 0.009618 | 0.000864 |
| 5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.769382 | 0.195368 | 0.032496 | 0.002754 |
| 5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.798371 | 0.173323 | 0.026215 | 0.002091 |
| 5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.876957 | 0.114977 | 0.008066 |
| 5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4 | 0.000000 | 0.619763 | 0.256759 | 0.091331 | 0.026183 | 0.005375 | 0.000589 |
| 4,10 | 0.000000 | 0.000000 | 0.647934 | 0.250930 | 0.079930 | 0.018752 | 0.002454 |
| 4,9 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,8 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6 | 0.000000 | 0.000000 | 0.687719 | 0.234612 | 0.063990 | 0.012405 | 0.001274 |
| 4,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.722581 | 0.221643 | 0.049624 | 0.006153 |
| 4,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.772414 | 0.190903 | 0.033563 | 0.003120 |
| 4,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.816667 | 0.164832 | 0.018502 |
| 4,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5 | 0.000000 | 0.000000 | 0.666100 | 0.244772 | 0.072316 | 0.015152 | 0.001660 |
| 4,5,10 | 0.000000 | 0.000000 | 0.000000 | 0.698752 | 0.234682 | 0.058434 | 0.008131 |
| 4,5,9 | 0.000000 | 0.000000 | 0.000000 | 0.719927 | 0.224997 | 0.049645 | 0.005432 |
| 4,5,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.758221 | 0.208531 | 0.033248 |
| 4,5,8 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6 | 0.000000 | 0.000000 | 0.000000 | 0.745247 | 0.209635 | 0.041004 | 0.004114 |
| 4,5,6,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.786359 | 0.188851 | 0.024790 |
| 4,5,6,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.813278 | 0.170376 | 0.016346 |
| 4,5,6,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.862486 | 0.137514 |
| 4,5,6,8 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.845739 | 0.142050 | 0.012211 |
| 4,5,6,8,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.899083 | 0.100917 |
| 4,5,6,8,9 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.934446 | 0.065554 |
| 4,5,6,8,9,10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
Если вы планируете попытаться повторить мою работу, вот несколько советов по переходу из одного состояния в другое. Начните с состояний, близких к концу, в которых стрелок уже набрал 5 очков. Например, если стрелку нужно всего 4 очка, то могут произойти три вещи: (1) Он набирает и набирает 4 очка, (2) Он набирает и набирает уже набранное очко, (3) Он набирает семерку. Вероятность (1) равна (3/24)*(1/3) = 1/24 = 0,041667. Вероятность (2) равна (4/24)*(2/5) + (5/24)*(5/11) + (5/24)*(5/11) + (4/24)*(2/5) + (3/24)*(1/3) = 0,364394. Вероятность события (3) равна 1 - 0,041667 - 0,364394 = 0,593939. В конечном итоге произойдет событие (1) или (3). Вероятность того, что (1) произойдет раньше (3), равна 0,041667/(0,041667 + 0,593939) = 0,065554. Рекурсивно вернитесь к начальной точке. Это либо займет много времени, будет избыточным и скучным, либо вы можете сделать это в электронной таблице в автоматическом режиме.
Исчисление
Первый шаг в этом методе — вычисление вероятности всех 7 возможных соответствующих исходов ставки на линию «пас» после установления точки. Мы можем игнорировать 12 комбинаций, или 1/3 шанса, выигрыша или проигрыша игрока сразу после первого броска, поскольку эти события не имеют значения для ставки «Огонь». Таким образом, первый бросок основан на 24 возможных комбинациях, а не на 36.
- Набранные и выигранные 4 очка = (3/24) × (3/9) = 1/24 = приблизительно 4,17%
- Набрано и выиграно 5 очков = (4/24) × (4/10) = 1/15 = приблизительно 6,67%
- Набранное и выигранное очко из 6 = (5/24) × (5/11) = 25/264 = приблизительно 9,47%
- 8 набранных и выигранных очков = (5/24) × (5/11) = 25/264 = приблизительно 9,47%
- Набранное и выигранное очко из 9 = (4/24) × (4/10) = 1/15 = приблизительно 6,67%
- Набрано и выиграно 10 очков = (3/24) × (3/9) = 1/24 = приблизительно 4,17%
- Любое набранное очко и 7 очков = 2×((3/24) × (6/9))+ 2× ((4/24) × (6/10)) + 2×((5/24) × (6/11)) = 98/165 = приблизительно 59,39%
Обратите внимание, что сумма этих вероятностей равна 1.
Далее, вместо того чтобы исход ставки на «Огненную ставку» определялся броском двух игральных костей по очереди, предположим, что промежуток времени между событиями происходит случайным образом, подчиняясь экспоненциальному распределению со средним значением в одну единицу времени между событиями. Если событие происходит, то оно будет подчиняться вероятностям, рассчитанным нами ранее для игры в крэпс.
Например, вероятность выигрыша с результатом 0,4 составляет 1/24. Таким образом, среднее время между выигрышами с результатом 0,4 составит 24 единицы. Вероятность того, что пройдет x единиц времени без выигрыша с результатом 0,10, равна exp(-x/24). В качестве дополнения, вероятность хотя бы одного выигрыша с результатом 0,10 за x единиц времени равна 1-exp(-x/24).
Для определения победителя в «Огненной ставке» не имеет значения, сколько времени прошло между событиями — важно, какие это события. Таким образом, для определения победителя ставки мы можем использовать интеграл по всему времени следующим образом:
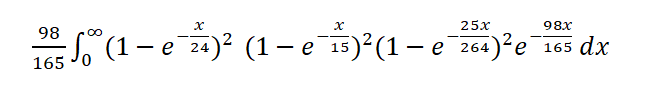
Позвольте мне объяснить, что означает этот интеграл. Это вероятность того, что по истечении x единиц времени был хотя бы один выигрыш каждого числа, кроме 7. Поскольку вероятность выигрыша 0,4 и 0,10 одинакова, мы можем возвести вероятность выигрыша 0,4 в квадрат. То же самое для 5 и 9, а также 6 и 8. Наконец, мы умножаем все это на 98/165, вероятность выпадения семерки, чтобы закрыть ставку. Если бы мы этого не сделали, игрок мог бы получить выплату за несколько совпадающих выигрышей.
Интегрирование вручную было бы очень утомительным и чревато ошибками. К счастью, существуют калькуляторы интегралов . Чтобы использовать калькулятор для этой задачи, перейдите по ссылке и введите следующее в текстовое поле вверху: (1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25x/264))^2*exp(-98x/165)/(165/98). Затем нажмите «Параметры» и установите нижнюю границу равной 0, а верхнюю — бесконечности. После этого нажмите «Перейти».
Прежде чем рассматривать границы интегрирования, ответ равен (98*(-(165*e^(-(98*x)/165))/98+(2640*e^(-(839*x)/1320))/839+(330*e^(-(109*x)/165))/109-(220*e^(-(149*x)/220))/149+(880*e^(-(303*x)/440))/303-(1760*e^(-(309*x)/440))/309-(11* e^(-(8*x)/11))/8-(1320*e^(-(241*x)/330))/241+(1320*e^(-(491*x)/660))/491-(5280*e^(-(99) 7*x)/1320))/997+(528*e^(-(203*x)/264))/203+(2640*e^(-(1019*x)/1320))/1019-(60*e^(-(47*x) )/60))/47+(2640*e^(-(263*x)/330))/263-(132*e^(-(107*x)/132))/107+(528*e^(-(217*x)/264) )/217+(80*e^(-(33*x)/40))/33-(1760*e^(-(369*x)/440))/369+(40*e^(-(17*x)/20))/17-(88*e^( -(19*x)/22))/19-(15*e^(-(13*x)/15))/13-(480*e^(-(107*x)/120))/107+(528*e^(-(239*x)/264) )/239-(12*e^(-(11*x)/12))/11+(15*e^(-(14*x)/15))/7+(48*e^(-(23*x)/24))/23-e^(-x)))/165.
К счастью, этот калькулятор позволяет учитывать границы интегрирования и выдает решение в виде 3700403899126040038831518494284887738125 / 22780863797678919004236184338193605974839452, что приблизительно равно 0,0001624347492698264.
Конечно, это всего лишь вероятность попадания во все шесть точек, но ту же логику можно использовать для нахождения вероятности попадания в любое количество точек. Оставляю это на самостоятельное изучение читателю ;-).
Внешние ссылки
- Математические аспекты Fire Bet обсуждаются на моём сопутствующем сайте Wizard of Vegas.
- Посмотрите мою собственную электронную таблицу , которую я разместил в Google Docs, и любой желающий может её скачать.
- В книге Стюарта Н. Этьера «Доктрина случайности: вероятностные аспекты азартных игр» обсуждается математика игры Fire Bet.
Благодарности
Хочу поблагодарить участника форума Wizard of Vegas Ace2 за его неустанные советы по вычислению вероятности ставки «Огонь» с помощью интегрирования.



