На этой странице
Эксперимент с органической рулеткой
Введение
В сентябре 2016 года я услышал обвинение в адрес игровых автоматов Organic Roulette производства компании Interblock в том, что они принимают агрессивные меры против игроков, пытающихся обмануть систему. Как сторонник честной и справедливой азартной игры, я обратил на эту тему внимание. В течение шести месяцев я посещал множество встреч, посвященных этой теме, и собрал данные о тысячах вращений барабанов. На этой странице рассказывается история расследования.
Игра
Автомат «Органическая рулетка» можно найти во многих казино Лас-Вегаса. Он работает так же, как и настольная игра. У игрока есть около 30 секунд, чтобы сделать ставку. Обычно шарик вылетает, когда у игрока остается от 1 до 5 секунд, чтобы сделать ставку. После того, как ставки сделаны, потребуется еще несколько секунд, чтобы шарик остановился. Затем выплачиваются выигрыши, и весь процесс повторяется. От начала до конца игра занимает чуть больше минуты.
Обвинение
Выиграть в эту игру возможно, если между броском шарика и закрытием приема ставок проходит достаточно времени. Скорость шарика и колеса можно проанализировать до закрытия приема ставок. Контролеры колеса могут оценить скорость шарика, колеса и его положение в момент запуска, чтобы определить, где именно на колесе приземлится шарик.
Я буду называть игрока, обратившего мое внимание на эту проблему, г-ном С. По его словам, для любителей игра, вероятно, была бы честной, где вероятность выигрыша каждого числа составляла бы 1 к 38. Однако, если бы возникли определенные проблемы, игра перешла бы в то, что он назвал «режимом угрозы». Предполагаемые проблемы для игрока, устанавливающего счетчик очков на колесе, заключались в следующем:
- Крупные ставки. Было неясно, насколько большой должна быть эта «крупная» ставка, но 20 долларов в общей сложности было сочтено достаточной суммой.
- Ставки в последний момент. А точнее, пять секунд между запуском мяча и закрытием временного окна.
- Ставки по секциям. Ставки на отдельные числа, расположенные близко друг к другу на колесе.
В случае, если игра чувствовала угрозу, автомат якобы предпринимал агрессивные контрмеры. Цель этих контрмер заключалась в том, чтобы заставить шарик остановиться не в той зоне, на которую сделал ставку оператор колеса. Как это делалось, было неясно, но у г-на С. были некоторые теории, которыми он попросил меня не делиться.
Г-н С. поделился со мной своими данными и их анализом, что, безусловно, пробудило во мне интерес. Однако г-н С. попросил меня не разглашать никаких подробностей.
Глобальная игровая выставка
На начальном этапе моего участия в этом деле я посетил выставку Global Gaming Expo 2016 в Лас-Вегасе. Компания Interblock занимала там очень большую и заметную позицию. С разрешения г-на С. я попросил поговорить с инженером на стенде Interblock. Продавщица, с которой я сначала общался, нашла инженера, который подошел и представился. Меня посадили за автомат, похожий на Organic Roulette, который также давал игроку около пяти секунд после запуска шарика, чтобы закончить делать ставки. После знакомства разговор примерно такой (я пересказываю):
- Шеклфорд: Я заметил, что на этом автомате шарик выпускается за несколько секунд до того, как прекращается прием ставок.
- Межблок: И что?
- Шеклфорд: Вам не кажется, что это будет уязвимо для команд, занимающихся хронометражем?
- Interblock: Мы прекрасно осведомлены об этой проблеме.
По его поведению и тону было ясно, что он больше ничего не скажет, поэтому я поблагодарил его за уделенное время и пошел своей дорогой.
Делайте выводы из этого разговора, что хотите.
Первый эксперимент
После презентации г-на С. я, безусловно, заинтересовался происходящим. В качестве первого шага я собрал данные по 299 вращениям барабанов вместе с еще одним заинтересованным лицом, которого я буду называть г-ном С. Наш метод ставок заключался в том, чтобы каждый делал ставку в 2 доллара на пять последовательных чисел. Г-н С. не был уверен, будет ли достаточно 10 долларов общих ставок, чтобы игра почувствовала угрозу, но посчитал, что это хороший баланс между тем, чтобы разозлить игру, и тем, чтобы не потерять слишком много денег во время эксперимента.
Ни я, ни мистер С не умеем рассчитывать время вращения колеса, поэтому мы делали ставки систематически, устанавливая центр дуги ставки таким образом, чтобы выигрышное число на втором вращении соответствовало выигрышной позиции. Цель заключалась в том, чтобы сравнить выигрышную позицию на колесе с центром нашей дуги ставок.
На графике 1 и в таблице 1 показана частота каждого смещения между положением нашей центральной позиции для ставок и выигрышным номером.
png" />Таблица 1
| Компенсировать | Наблюдения | Ожидания |
|---|---|---|
| -18 | 5 | 7.87 |
| -17 | 9 | 7.87 |
| -16 | 13 | 7.87 |
| -15 | 7 | 7.87 |
| -14 | 11 | 7.87 |
| -13 | 12 | 7.87 |
| -12 | 7 | 7.87 |
| -11 | 10 | 7.87 |
| -10 | 8 | 7.87 |
| -9 | 10 | 7.87 |
| -8 | 6 | 7.87 |
| -7 | 8 | 7.87 |
| -6 | 9 | 7.87 |
| -5 | 10 | 7.87 |
| -4 | 3 | 7.87 |
| -3 | 7 | 7.87 |
| -2 | 7 | 7.87 |
| -1 | 6 | 7.87 |
| 0 | 8 | 7.87 |
| 1 | 4 | 7.87 |
| 2 | 4 | 7.87 |
| 3 | 8 | 7.87 |
| 4 | 7 | 7.87 |
| 5 | 4 | 7.87 |
| 6 | 18 | 7.87 |
| 7 | 6 | 7.87 |
| 8 | 9 | 7.87 |
| 9 | 6 | 7.87 |
| 10 | 8 | 7.87 |
| 11 | 4 | 7.87 |
| 12 | 13 | 7.87 |
| 13 | 3 | 7.87 |
| 14 | 8 | 7.87 |
| 15 | 12 | 7.87 |
| 16 | 6 | 7.87 |
| 17 | 7 | 7.87 |
| 18 | 9 | 7.87 |
| 19 | 7 | 7.87 |
| Общий | 299 | 299.00 |
Критерий согласия хи-квадрат дает значение хи-квадрат, равное 45,29 при 37 степенях свободы. Вероятность того, что случайная игра даст результаты, более искаженные, чем это значение, составляет 16,5%.
В таблице 2 представлены результаты теста Гаусса для различных размеров дуги, центрированных вокруг центрального числа, на которое была сделана ставка в первом эксперименте. Для рассмотренной нами дуги из пяти чисел ожидаемое количество выигрышей на честном колесе составило бы 39,3. У нас получилось всего 29. Вероятность таких плохих или еще худших результатов в честной игре составляет 3,84%.
Таблица 2
| Размер дуги | Наблюдения | Ожидания | Стандартный размер. Отклонение | Число Стандарт Отклонение | Вероятность |
|---|---|---|---|---|---|
| 1 | 8 | 7.87 | 2.77 | 0,05 | 0.518957 |
| 3 | 18 | 23.61 | 4.66 | -1.20 | 0.114658 |
| 5 | 29 | 39.34 | 5.85 | -1.77 | 0.038417 |
| 7 | 44 | 55.08 | 6.70 | -1.65 | 0.049187 |
| 17 | 124 | 133.76 | 8.60 | -1.14 | 0.128074 |
Хотя наши результаты, безусловно, не оправдали ожиданий, это вполне могло быть просто обычным невезением. Однако я подсчитал, что если я буду проигрывать с той же частотой, то для доказательства нечестной игры потребуется просто увеличить размер выборки. После многочисленных встреч и переписки было решено провести второй эксперимент.
Второй эксперимент
Чтобы убедительно доказать нечестность азартной игры в казино, эксперимент должен быть воспроизводимым. После долгих обсуждений было решено проверить наличие дефицита выигрышей, делая ставки по 5 долларов на каждое число в пятичисловой дуге. Было решено провести 1000 вращений на трех разных колесах. Помимо г-на С., всегда присутствовал как минимум один свидетель, либо я, либо г-н С. Было решено, что после завершения игры мы изучим данные и решим, что делать дальше. Если бы нам показалось, что игра не является случайной, и это было бы неопровержимо доказано, мы планировали бы обнародовать наши доказательства.
На момент завершения этой истории у нас было 1204 вращения данных. Мы знали, что результаты немного не оправдали ожиданий, но, по словам г-на С., игры большую часть времени работали случайным образом, а в «угрозовом» режиме — лишь иногда.
На основании анализа данных мы пришли к выводу, что проигрывали недостаточно часто, чтобы оправдать продолжение игр.
Ниже представлены результаты и анализ второго эксперимента. Для начала, на следующем графике и в таблице 3 показана частота каждого смещения между центром дуги ставки и местом приземления мяча.
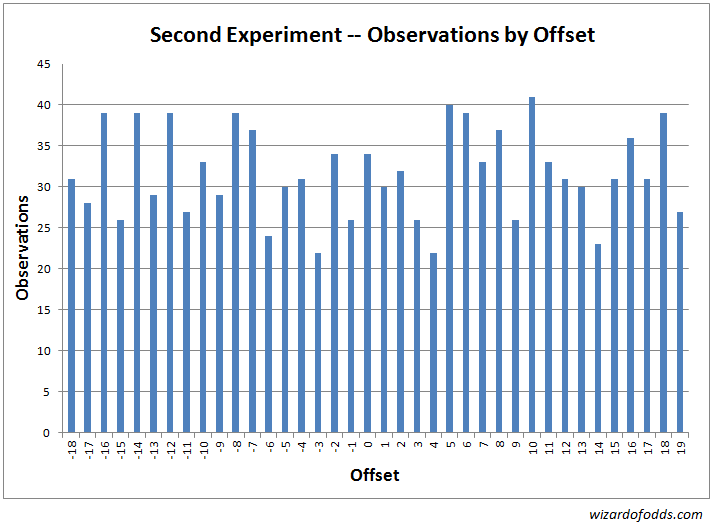
Таблица 3
| Компенсировать | Наблюдения | Ожидания |
|---|---|---|
| -18 | 31 | 31.68 |
| -17 | 28 | 31.68 |
| -16 | 39 | 31.68 |
| -15 | 26 | 31.68 |
| -14 | 39 | 31.68 |
| -13 | 29 | 31.68 |
| -12 | 39 | 31.68 |
| -11 | 27 | 31.68 |
| -10 | 33 | 31.68 |
| -9 | 29 | 31.68 |
| -8 | 39 | 31.68 |
| -7 | 37 | 31.68 |
| -6 | 24 | 31.68 |
| -5 | 30 | 31.68 |
| -4 | 31 | 31.68 |
| -3 | 22 | 31.68 |
| -2 | 34 | 31.68 |
| -1 | 26 | 31.68 |
| 0 | 34 | 31.68 |
| 1 | 30 | 31.68 |
| 2 | 32 | 31.68 |
| 3 | 26 | 31.68 |
| 4 | 22 | 31.68 |
| 5 | 40 | 31.68 |
| 6 | 39 | 31.68 |
| 7 | 33 | 31.68 |
| 8 | 37 | 31.68 |
| 9 | 26 | 31.68 |
| 10 | 41 | 31.68 |
| 11 | 33 | 31.68 |
| 12 | 31 | 31.68 |
| 13 | 30 | 31.68 |
| 14 | 23 | 31.68 |
| 15 | 31 | 31.68 |
| 16 | 36 | 31.68 |
| 17 | 31 | 31.68 |
| 18 | 39 | 31.68 |
| 19 | 27 | 31.68 |
| Общий | 1204 | 1204.00 |
Критерий согласия хи-квадрат дает значение хи-квадрат, равное 34,79 при 37 степенях свободы. Вероятность того, что случайная игра даст результаты, более искаженные, чем это значение, составляет 57,32%.
В таблице 4 представлены результаты теста Гаусса для различных размеров дуг, центрированных вокруг центрального числа ставки. Все размеры дуг находятся в пределах нормального диапазона.
Таблица 4
| Размер дуги | Наблюдения | Ожидания | Стандартный размер. Отклонение | Число Стандарт Отклонение | Вероятность |
|---|---|---|---|---|---|
| 1 | 34 | 31.68421053 | 5.55 | 0,42 | 0.661637 |
| 3 | 90 | 95.05263158 | 9.36 | -0.54 | 0.294599 |
| 5 | 156 | 158.4210526 | 11.73 | -0.21 | 0.418235 |
| 7 | 204 | 221.7894737 | 13.45 | -1.32 | 0.092997 |
| 17 | 536 | 538.6315789 | 17.25 | -0.15 | 0.439385 |
Сводные результаты
Ниже приведены объединенные данные первого и второго экспериментов. Для начала, на следующем графике и в таблице 5 показана частота каждого смещения между центром дуги ставки и местом приземления мяча.
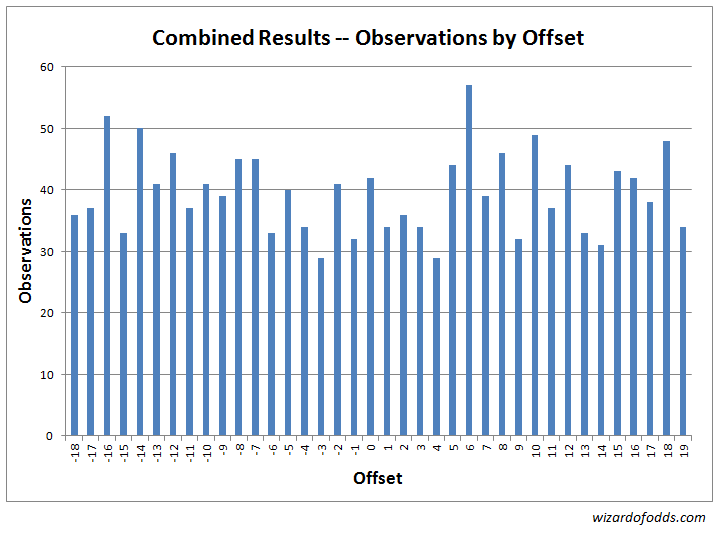
Таблица 5
| Компенсировать | Наблюдения | Ожидания |
|---|---|---|
| -18 | 36 | 39.55 |
| -17 | 37 | 39.55 |
| -16 | 52 | 39.55 |
| -15 | 33 | 39.55 |
| -14 | 50 | 39.55 |
| -13 | 41 | 39.55 |
| -12 | 46 | 39.55 |
| -11 | 37 | 39.55 |
| -10 | 41 | 39.55 |
| -9 | 39 | 39.55 |
| -8 | 45 | 39.55 |
| -7 | 45 | 39.55 |
| -6 | 33 | 39.55 |
| -5 | 40 | 39.55 |
| -4 | 34 | 39.55 |
| -3 | 29 | 39.55 |
| -2 | 41 | 39.55 |
| -1 | 32 | 39.55 |
| 0 | 42 | 39.55 |
| 1 | 34 | 39.55 |
| 2 | 36 | 39.55 |
| 3 | 34 | 39.55 |
| 4 | 29 | 39.55 |
| 5 | 44 | 39.55 |
| 6 | 57 | 39.55 |
| 7 | 39 | 39.55 |
| 8 | 46 | 39.55 |
| 9 | 32 | 39.55 |
| 10 | 49 | 39.55 |
| 11 | 37 | 39.55 |
| 12 | 44 | 39.55 |
| 13 | 33 | 39.55 |
| 14 | 31 | 39.55 |
| 15 | 43 | 39.55 |
| 16 | 42 | 39.55 |
| 17 | 38 | 39.55 |
| 18 | 48 | 39.55 |
| 19 | 34 | 39.55 |
| Общий | 1503 | 1503.00 |
Критерий согласия хи-квадрат дает значение хи-квадрат, равное 41,75 при 37 степенях свободы. Вероятность того, что случайная игра даст результаты, более искаженные, чем это значение, составляет 27,19%.
В таблице 6 представлены результаты теста Гаусса для различных размеров дуг, центрированных вокруг центрального числа ставки. Все результаты тестов находятся в пределах разумного диапазона для честной игры.
Таблица 6
| Размер дуги | Наблюдения | Ожидания | Стандартный размер. Отклонение | Число Стандарт Отклонение | Вероятность |
|---|---|---|---|---|---|
| 1 | 42 | 39.55263158 | 6.21 | 0,39 | 0.653346 |
| 3 | 108 | 118.6578947 | 10.45 | -1.02 | 0.153986 |
| 5 | 185 | 197.7631579 | 13.11 | -0.97 | 0.165050 |
| 7 | 248 | 276.8684211 | 15.03 | -1.92 | 0.027374 |
| 17 | 660 | 672.3947368 | 19.28 | -0.64 | 0.260114 |
Коэффициент корреляции между результатами первого и второго экспериментов составляет 0,153853. Проще говоря, это означает, что наблюдалась слабая корреляция, но в пределах ожидаемых значений для двух случайных наборов данных.
Заключение
Прежде чем заявить о нечестности какой-либо игры, я должен представить очень убедительные доказательства. В данном случае эти доказательства не были предоставлены. Другими словами, у меня нет оснований обвинять игровые автоматы Organic Roulette в нечестной игре.
Ответы
Я предложил г-ну С. возможность предварительно ознакомиться с этой страницей, прежде чем объявить о ней широкой публике. Он внес много полезных предложений и исправлений. В конце концов, у него все еще остались некоторые претензии к формулировкам. Поэтому я дал ему возможность опубликовать ответ, что он и сделал. Он озаглавлен «Другой взгляд на результаты эксперимента Interblock от г-на С.».
Мне всегда хочется сказать последнее слово, поэтому я опубликовал контр-ответ под названием « Ответ на ответ г-на С. на эксперимент Майкла Шеклфорда с органической рулеткой» .



