На этой странице
Приложение Сик Бо
На этой странице
Введение

Изображение взято из свода правил отеля/казино Claridge.
Бонусы за онлайн-игры Sic Bo Посмотреть все
- Низкий :
Эта ставка не имела бы преимущества казино, если бы не исключение для тройного выигрыша. Вероятность выпадения тройки 1, 2 или 3 составляет 3/216. Вероятность выпадения любой суммы от 3 до 10 составляет 1/2, или 108/216. Таким образом, вероятность выигрышной тройки составляет 108/216 - 3/216 = 105/216. Преимущество игрока, следовательно, составляет (105/216)*(+1) + (111/216)*(-1) = -6/216 ≈ -2,78%.
- Высокий : см. Низкий.
- Конкретный номер :
Вероятность выпадения нуля или определенного числа равна (5/6) ³ = 125/216.
Вероятность выпадения одного из определённых чисел равна 3 * (1/6) ¹ * (5/6) ² = 75/216.
Вероятность выпадения двух одинаковых чисел равна 3 * (1/6) ² * (5/6) ¹ = 15/216.
Вероятность выпадения трех одинаковых чисел равна (1/6) ³ = 1/216.
Таким образом, преимущество игрока составляет (125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = -17/216 ≈ -7,780%. - Всего 4 :
Выпадение числа 4 возможно тремя способами: (1+1+2, 1+2+1, 2+1+1). Таким образом, преимущество игрока составляет 3/216*(+60) + (213/216)*(-1) = -33/216 = -15,278%.
- Всего 5 :
Существует 6 способов выбросить 5: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1). Таким образом, преимущество игрока составляет 6/216*(+30) + (210/216)*(-1) = -30/216 = -13,889%.
- Всего 6 :
Существует 10 способов выбросить 6: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1, 3+1+2, 3+2+1, 2+2+2). Таким образом, преимущество игрока составляет 10/216*(+17) + (206/216)*(-1) = -36/216 = -16,667%.
- Всего 7 :
Существует 15 способов выбросить 7: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1, 4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2). Таким образом, преимущество игрока составляет 15/216*(+12) + (201/216)*(-1) = -21/216 = -9,722%.
- Всего 8 :
Существует 21 способ выбросить 8: (1-6-6 * 3 способа, 1-2-5 * 6 способов, 1-3-4 * 6 способов, 2-2-4 * 3 способа, 2-3-3 * 3 способа). Таким образом, преимущество игрока составляет 21/216*(+8) + (195/216)*(-1) = -27/216 = -12,500%.
- Всего 9 :
Существует 25 способов выбросить 9: (1-2-6 * 6 способов, 1-3-5 * 6 способов, 1-4-4 * 3 способа, 2-2-5 * 3 способа, 2-3-4 * 6 способов, 3-3-3 * 1 способ). Таким образом, преимущество игрока составляет 25/216*(+6) + (191/216)*(-1) = -41/216 = -18,982%.
- Всего 10 :
Существует 27 способов выбросить 10: (1-3-6 * 6 способов, 1-4-5 * 6 способов, 2-2-6 * 3 способа, 2-3-5 * 6 способов, 2-4-4 * 3 способа, 3-3-4 * 3 способа). Таким образом, преимущество игрока составляет 27/216*(+6) + (189/216)*(-1) = -27/216 = -12,500%.
- Всего 11 : См. общее количество 10
- Всего 12 : См. общее количество 9
- Всего 13 : См. общее количество 8
- Всего 14 : См. всего 7
- Всего 15 : См. всего 6
- Всего 16 : См. общее количество 5
- Всего 17 : См. всего 4
- Два числа :
Предположим, выбраны два числа: 1 и 2. Существует 30 комбинаций, включающих 1 и 2: 1-2-1 * 3 способа, 1-2-2 * 3 способа, 1-2-3 * 6 способов, 1-2-4 * 6 способов, 1-2-5 * 6 способов, 1-2-6 * 6 способов. Таким образом, преимущество игрока составляет 30/216*(+5) +(186/216)*(-1) = -36/216 = -16,667%.
- Конкретная триплетная последовательность :
Существует только один способ выбросить определённую тройку. Таким образом, преимущество игрока составляет 1/216*(+180) + (215/216)*(-1) = -35/216 = -16,20%.
- Любая тройка :
Существует 6 способов выбросить тройку. Таким образом, преимущество игрока составляет 6/216*(+30) +(210/216)*(-1) = -30/216 = -13,889%.
- Конкретная пара :
Предположим, выбранная пара — это единицы. Существует 16 способов выпадения двух или трех одинаковых чисел: 1+1+1, 1+1+2 * 3 способа, 1+1+3 * 3 способа, 1+1+4 * 3 способа, 1+1+5 * 3 способа, 1+1+6 * 3 способа. Таким образом, преимущество игрока составляет 16/216*(+10) + (200/216)*(-1) = -72/216 = -18,52%.
Ниже приведена формула для s точек на n кубиках, взятая из книги Ричарда А. Эпштейна « Теория азартных игр и статистическая логика» , формула 5-14.
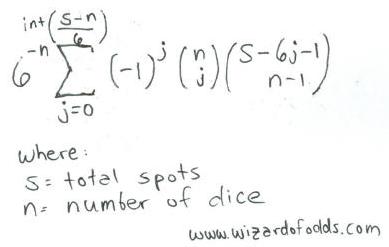
Например, давайте посмотрим, сколько способов получить 11 точек на 3 кубиках.
int[(sn)/6] = int[(11-3)/6] = int[1.33] = 1
Итого будет 6 -3 * [-1 0 *combin(3,0)*combin(11-6*0-1,3-1) + -1 1 *combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*комбинация(10,2) + -1*3*комбинация(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12,5%
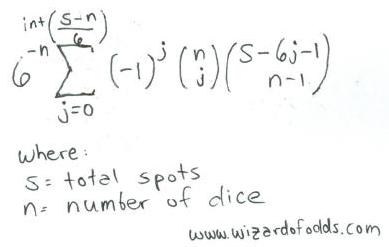










.png)










