WOO logo

Wizard рекомендует

Пазл из сложенных прямоугольников


В этом выпуске я представляю математическую головоломку из ноябрьского номера бюллетеня Mensa.

Рассмотрим прямоугольник размером 1х4. Теперь сложим этот прямоугольник так, чтобы противоположные углы совпадали, как показано на этом рисунке.

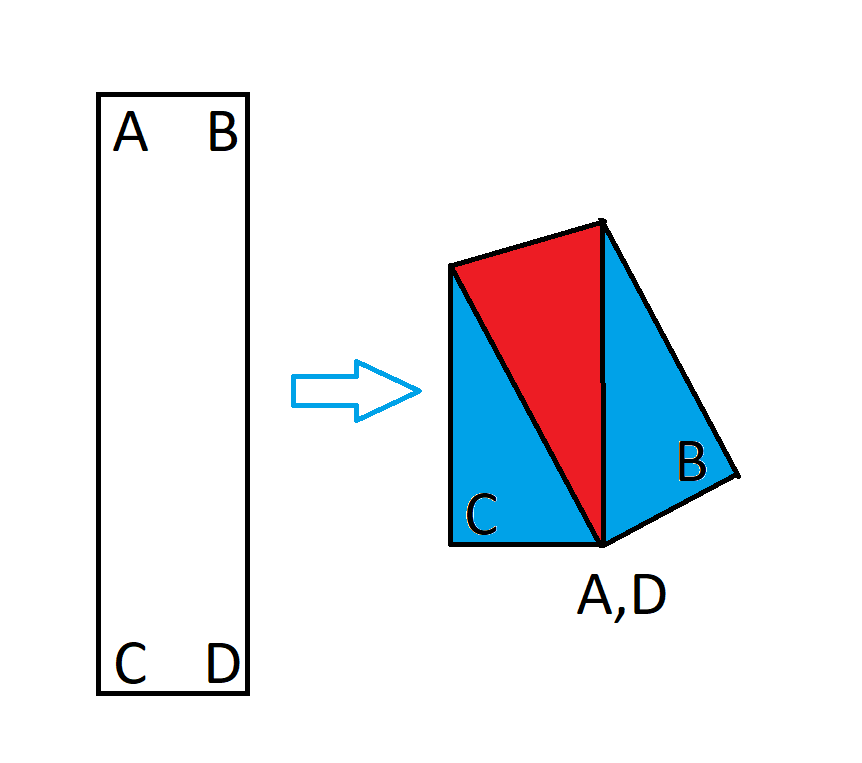
прямоугольник 1x4

После складывания прямоугольника получается неправильный пятиугольник. Каково отношение площади, где бумага перекрывает основной прямоугольник, к общей площади? Другими словами, отношение площади, выделенной красным цветом на изображении выше, к общей площади.

Прокрутите вниз, чтобы увидеть ответ и решение.

Отвечать

Ответ: 17/47 = приблизительно 0,3617

Решение

Чтобы объяснить решение, позвольте мне определить еще несколько точек, как показано на следующем изображении. F — середина отрезка E и G.

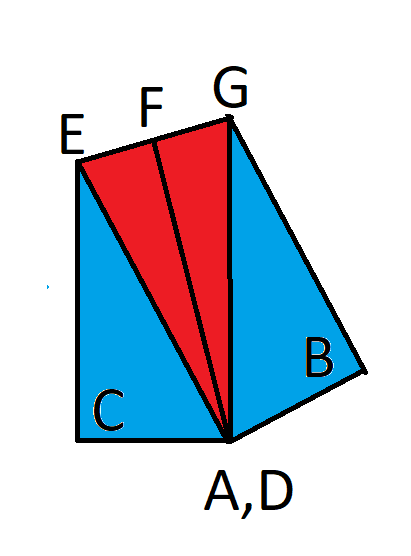
Прямоугольник 1x4, пятиугольник - решение

Мы знаем:

AC = 1

CE + AE = 4

Решим уравнение относительно AE, используя теорему Пифагора:

1 2 + (CE) 2 = (AE) 2

Подставив 4 – CE вместо AE, получаем:

1 2 + (CE) 2 = (4 – CE) 2

1 + (ЦЭ) 2 = 16 – 8 (ЦЭ) + (ЦЭ) 2

8(CE) = 15

CE = 15/8

Возвращаясь к уравнению 1 2 + (CE) 2 = (AE) 2 , мы можем решить его относительно (AE), поскольку нам известно значение EC:

(AE) 2 = (CE) 2 + 1 2

(AE) 2 = (15/8) 2 + 1 2

(AE) 2 = 225/64 + 64/64

(AE) 2 = 289/64

6;font-family: 'Open Sans',sans-serif;color: #313131!important">AE = 17/8

До сгиба длина от A до D была диагональю прямоугольника. Снова используя теорему Пифагора, длина равна sqrt(17).

(AF) имеет половину этой длины, или sqrt(17)/2.

Зная AE и AF, мы можем найти EF, снова используя теорему Пифагора:

(AE) 2 = (EF) 2 + (AF) 2

(17/8) 2 = (EF) 2 + (sqrt(17)/2) 2

289/64 = (EF) 2 + 17/4

289/64 = (EF) 2 + 272/64

(EF) 2 = 17/64

EF = sqrt(17)/8

Как уже говорилось, F — середина отрезка E и G. E = 2*√17/8 =√17/4.

Красный треугольник, AEG = (1/2) × основание × высота =

= (1/2) × кв.(17/4) × кв.(17)/2

= (1/2) × (17/8) = 17/16

Площадь треугольника ACE = (1/2) * основание * высота =

(1/2) × 1 × (15/8) = 15/16.

Площадь всего пятиугольника = AEG + 2*ACE =

(17/16) + 2*(15/16) = 47/16

Таким образом, площадь красной области по отношению ко всему пятиугольнику равна

(17/16) / (47/16) = 17/47 = приблизительно 0,3617


Автор: Michael Shackleford