Доказательство делимости на 3

На этой неделе я немного отвлекусь от президентских викторин и попробую что-нибудь новенькое. Мне всегда нравились хорошие математические доказательства. Пока у меня не закончатся идеи, я буду разбирать некоторые известные математические теоремы и пытаться объяснить, почему они верны, как можно более простым языком. Для начала, на этой неделе я покажу, что если сумма цифр любого целого числа делится на 3, то и само число делится на 3. Однако, прежде чем мы перейдем к этому, я представлю обычную еженедельную логическую головоломку.

Логическая головоломка

На столе лежат четыре карты. Вы видите, что на лицевой стороне лежат карты с номерами D, K, 3 и 7. Вы знаете, что на одной стороне каждой карты есть буква, а на другой — цифра. Существует правило, согласно которому карта, на одной стороне которой буква D, должна иметь на другой — цифру 3. Какие две карты нужно перевернуть, чтобы убедиться, что это правило соблюдено?

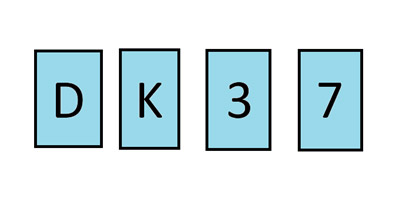
Ответ будет в конце информационного бюллетеня.

Доказательство делимости на 3

Как указано во введении, проверить, делится ли целое число на 3 без остатка, можно следующим образом:

1. Сложите цифры.
2. Если сумма, полученная по правилу 1, делится на 3 без остатка, то и исходное число будет делиться на 3 без остатка. Также, если сумма не делится на 3 без остатка, то и исходное число не будет делиться на 3 без остатка.

Рассмотрим, например, номер телефона Белого дома: 2024567041. Сумма цифр равна 2+0+2+4+5+6+7+0+4+1 = 31. Число 31 не делится на 3, следовательно, и исходное число не делится на 3.

Чтобы доказать работоспособность этого метода, разложим исходное число следующим образом:

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">2024567041 = (2*1000000000) + 0 + (2*10000000) + (4*1000000) + (5*100000) + (7*1000) + 0 + (4*10) + (1*1)

Далее разделим степень числа 10 на две части: единицу и остаток числа:

= (2*(999999999+1)) + 0 + (2*(9999999+1)) + (4*(999999+1)) + (5*(99999+1)) + (7*(9999+1)) + 0 + (4*(9+1)) + (1*(0+1))

Очевидно, что любое число, состоящее из одних девяток, делится на 3 без остатка. Например, 99999 = 3 * 33333.

Тем не менее, давайте переставим слагаемые в приведенном выше числе.

= (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) + (2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1)

Очевидно, что все семь членов первого ряда делятся на 3 без остатка, поскольку делятся на число, состоящее из одних девяток. Другими словами, (2*999999999) + (2*9999999) + (4*999999) + (5*99999) + (7*9999) + (4*9) + (1*0) делится на 9 без остатка, поэтому мы можем отбросить эту часть. В результате получаем:

(2*1) + (2*1) + (4*1) + (5*1) + (7*1) + (4*1) + (1*1) = 2+0+2+4+5+6+7+0+4+1 = 31

Это сумма цифр, равная 31. Поскольку оставшаяся часть не делится на 3 без остатка, то и целое число не может делиться на 3 без остатка.

Это же правило можно использовать и для проверки делимости на 9. Если сумма цифр исходного числа делится на 9, то и всё число будет делиться на 9. Верно и обратное: если сумма цифр не делится на 9 без остатка, то и всё число не будет делиться на 9 без остатка.

Решение логической головоломки

Назовём правило, согласно которому число 3 должно находиться на противоположной стороне от правила D, правилом «D-3».

1. • Очевидно, что мы должны перевернуть карту D, чтобы убедиться, что на другой стороне выпала тройка.
2. • На обратной стороне карточки K должен быть номер.Поскольку на другой стороне не может быть буквы D, эта карта не помогает нам опровергнуть правило D-3.
3. • На обратной стороне карты с цифрой 3 должна быть буква. Если это буква D, то правило D-3 выполняется. Если на обратной стороне есть любая другая буква, это нам не помогает. Таким образом, либо эта карта будет соответствовать правилу D-3, либо она не имеет значения. В любом случае, мы ищем карту, которая нарушает правило, чтобы опровергнуть правило D-3. Какая бы буква ни была на обратной стороне, она не опровергнет правило D-3. Поэтому проверять её не нужно.
4. • На обратной стороне карты с цифрой 7 должна быть буква. Если бы эта буква была D, то карта опровергла бы правило D-3. Поэтому необходимо проверить, не является ли она картой D-7, что было бы сокращением утверждения D-3.

Таким образом, проверять нужно только карты D и 7.