WOO logo

Wizard рекомендует

Парадокс дружбы (часть 1)

Парадокс дружбы гласит, что в среднем у ваших друзей больше друзей, чем у вас. Точнее, если взять среднее количество друзей всех ваших друзей, то это среднее значение, вероятно, будет больше, чем количество ваших друзей.

Казалось бы, это невозможно, но это правда.

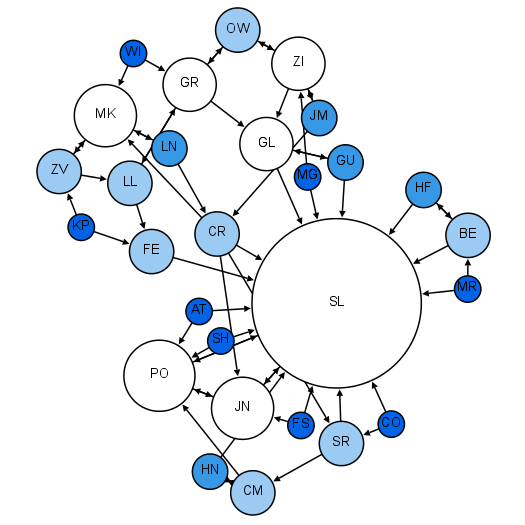
Авиапочта
Источник изображения: Википедия

В первой части исследования я провел два эксперимента. В обоих случаях у каждого человека был коэффициент харизмы, варьирующийся от 0 до 1. Вероятность того, что любые два человека подружатся, определялась как среднее значение коэффициентов харизмы.

Эксперимент №1

  1. Количество человек в группе = 25
  2. Коэффициент харизмы каждого человека = 0,5
  3. Размер симуляции = 35 миллионов
  4. Вероятность того, что у кого-то больше друзей, чем его друзей = 42,0%
  5. Вероятность того, что у человека столько же друзей, сколько у него друзей, составляет 1,2%.
  6. Вероятность того, что у кого-то меньше друзей, чем его друзей = 56,7%
  7. В среднем на одного человека приходится 12 друзей.
  8. Среднее количество друзей друзей = 12,5

Эксперимент №2

  1. Количество человек в группе = 25
  2. Коэффициент харизмы каждого человека = Случайный, выбранный из равномерного распределения от 0 до 1.
  3. Размер симуляции = 39 миллионов
  4. Вероятность того, что у кого-то больше друзей, чем его друзей = 48,1%
  5. Вероятность того, что у человека столько же друзей, сколько у него друзей, составляет 0,4%.
  6. Вероятность того, что у кого-то меньше друзей, чем его друзей = 51,4%
  7. Среднее количество друзей на человека = 15,544
  8. Среднее количество друзей друзей = 16,985

В обоих случаях «парадокс» подтвердился: у человека своих друзей больше, чем у него самого.

На следующей неделе я рассмотрю, почему этот кажущийся парадокс на самом деле верен.

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; "> Авиапочта
Источник изображения: Википедия

Дополнительная информация: страница Википедии о парадоксе дружбы.