Как обмануть правила рейтинга в шахматах

На этой неделе мы рассмотрим способ повышения рейтинга в шахматах с помощью формулы, позволяющей улучшить свой рейтинг, не улучшая при этом свою игру ни на йоту. Сразу предупреждаю, что это лишь небольшое преимущество, представляющее в основном академический интерес. Однако, прежде чем перейти к этому, как обычно, я представлю нашу еженедельную логическую головоломку.

Логическая головоломка

В очереди стоят 50 человек, пронумерованных от 1 до 50. Первый человек в очереди — номер 1. Каждый из них либо всегда говорит правду, либо всегда лжет. Все знают, правдивы ли слова других.

Все люди с четным числом говорят: «Все, кто передо мной, — лжецы».

Все люди с нечётными номерами говорят: «Все, кто идёт за мной, — лжецы».

Кто говорит правду?

Как обмануть правила рейтинга в шахматах

Насколько мне известно, наиболее распространенной шахматной рейтинговой системой является рейтинг Эло. Он назван в честь Арфада Эло. Эта же система используется и в других играх и видах спорта.

В принципе, принцип работы таков: формула определяет вероятность победы любого игрока в игре в зависимости от рейтингов обоих игроков. Победитель получает очки пропорционально вероятности поражения. Аналогично, проигравший игрок получает очки пропорционально вероятности победы. За победу начисляется одно очко, за ничью — 0,5, за ничью — 0.

Система основана на предположении, с которым я согласен, что результативность игрока можно смоделировать с помощью случайного числа, взятого на колоколообразную кривую, при этом рейтинг игрока является средним значением.Побеждает тот игрок, которому выпадет большее число.

Вероятность выигрыша определяется следующим образом:

Пусть r1 = рейтинг игрока 1.

Пусть r2 = рейтинг игрока 2.

p = Вероятность победы игрока 1.

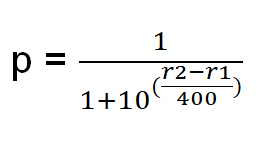
Рассмотрим пример. Пусть r1=1900 и r2=2000.

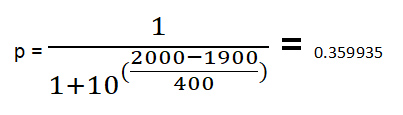
Предположим, за победу начисляется 1 балл, а за поражение — 0. Тогда повышение рейтинга составит 32 * (фактическое количество баллов – вероятность победы).

В приведенном выше примере, если игрок 1 проигрывает, как и предсказывается, то его рейтинг падает на 11,52 пункта, а рейтинг игрока 2 повышается на ту же величину. Если игрок 1 выигрывает, его рейтинг повышается на 20,48 пункта, а рейтинг игрока 2 понижается на ту же величину.

Система Эло основана на стандартном отклонении результатов, моделируемом описанным выше методом случайных чисел, равном 200. Я предполагаю, что это так. Однако формула вероятности выигрыша, на основе которой построены таблицы Эло, не соответствует такому стандартному отклонению, за исключением случаев, когда разница в рейтингах составляет 0 или 189.

Правильная вероятность того, что игрок с рейтингом r1 выиграет, составляет:

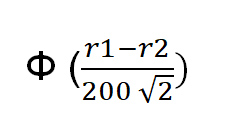
Где функция Φ(x) = вероятность того, что случайная стандартная нормальная переменная меньше x. В Excel правильная формула выглядит так: norm.s.dist((r1-r2)/(200*sqrt(2)),1).

Рассмотрим случай, когда разница в рейтингах составляет 100. Допустим, игрок 1 — аутсайдер. Формула Эло предполагает, что у игрока 1 35,99% шансов на победу. Однако его фактическая вероятность, основанная на стандартном отклонении результатов в 200, составляет 36,18%. Другими словами, победа игрока 1 — это хорошая ставка, а для игрока 2 — плохая. Я показываю, что ожидаемый прирост рейтинга игрока 1 и ожидаемый проигрыш игрока 2 составляют 0,06 пункта.

Теперь рассмотрим разницу в рейтингах в 300 пунктов, где игрок 1 является аутсайдером. В этом случае формула Эло дает игроку 1 15,10% шансов на победу, тогда как я показываю 14,44%. Это делает ставку на победу плохой для игрока 1 и хорошей для игрока 2. Ожидаемый проигрыш для игрока 1 составляет 0,21 пункта, как и ожидаемый выигрыш для игрока 2.

Математические вычисления, лежащие в основе фактических вероятностей, основаны на гауссовой кривой и гораздо сложнее, чем я хотел бы вдаваться в подробности в этом информационном бюллетене.

В итоге, если разница в рейтингах превышает 189, то для фаворита ставка на победу будет выгодной. Аналогично, если она меньше 189, то для аутсайдера ставка на победу будет выгодной.

Однако предвзятость довольно незначительна. Я бы не стал принимать или отклонять партии, основываясь на этой информации. Скорее, я считаю, что любую партию следует принимать из любви к шахматам.

Дополнительная информация: статья в Википедии о системе рейтинга Эло.

Ответ на логическую головоломку

Только люди № 2 и № 49 говорят правду.

Решение логической головоломки

Начнём с человека 1. Если он говорит правду, то все остальные лгут. Однако человек 3 утверждает, что все, от 4 до 50, лгут.Если это так, то человек 3 говорит правду. Однако человек 1 утверждает, что лжет. Это приводит к противоречию. Следовательно, человек 1 должен лгать.

Второй человек говорит лишь, что первый человек лжет. Это делает второго человека правдивым.

Каждый человек с четным числом от 4 до 50 утверждает, что человек 2 лжет. Это означает, что все они лжецы.

Человек 49 утверждает, что человек 50 лжет, что правда. Это делает человека 49 правдивым.

Каждый человек с нечетным номером от 3 до 47 утверждает, что человек 49 лжет. Это означает, что все они лжецы.

Таким образом, правду говорят только люди под номерами 2 и 49.