WOO logo

Wizard рекомендует

Доказательство теоремы о вписанном угле (часть 1)

На этой неделе мы возвращаемся к моей теме доказательства математической теоремы. На этой неделе речь пойдёт о теореме о вписанном угле. Доказательство более сложное, чем обычно, поэтому я разделю его на две части, вторая часть будет на следующей неделе. Однако, прежде чем мы перейдём к ней, я представлю свою обычную еженедельную логическую головоломку.

Логическая головоломка

На приведенной ниже схеме переместите одну монету так, чтобы образовались две линии по четыре монеты в каждой.

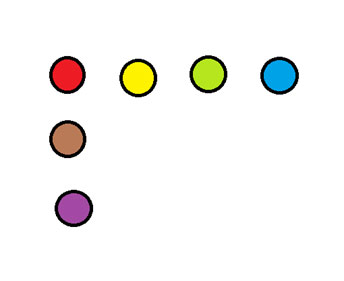
диаграмма

Ответ находится в конце информационного бюллетеня.

Доказательство теоремы о вписанном угле (часть 1)

Прежде чем объяснить теорему о вписанном угле, позвольте мне определить несколько точек на окружности на следующей диаграмме.

круг

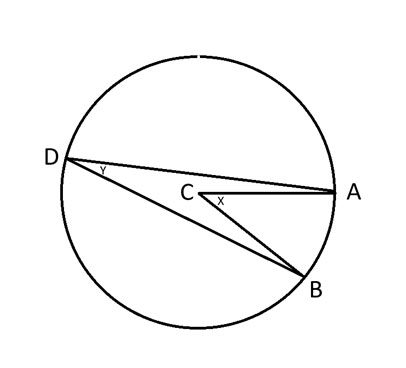
A, B и D = любые три точки на окружности.

C = Центр окружности.

x = Угол ACB.

y = Угол ADB.

Теорема о вписанном угле гласит, что угол 2y = x.

6; font-family: 'Open Sans', sans-serif; color: #313131 !important; ">В этом информационном бюллетене я постараюсь доказать это на примере конкретного случая, когда AD или BD образуют диаметр окружности. На следующей неделе я подробнее расскажу об этом на примере общего случая расположения D.

Назовём конкретный случай, когда AD образует диаметр окружности, случаем 1. Вот новая диаграмма для этого случая.

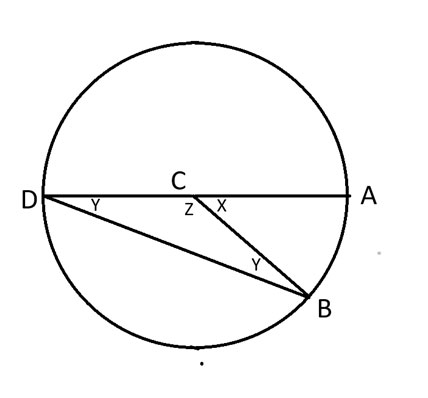
диаграмма рекламы

На приведенной выше диаграмме AD образует диаметр окружности с точкой C в центре.

Можно сказать, что x+z = 180 градусов, потому что они составляют половину от общего числа 360 градусов круга.

BCD образует равнобедренный треугольник. Следовательно, угол CDB = CBD = y.

Как было доказано в моей рассылке от 13 ноября 2025 года, сумма внутренних углов треугольника равна 180 градусам. Другими словами, z + 2y = 180 градусов.

Перепишем оба уравнения:

z = 180 – x

z = 180 – 2y

Давайте уравним оба значения, поскольку оба равны z.

180 – x = 180 – 2y

-x = -2y

x = 2y.

Итак, мы доказали частный случай теоремы о вписанном угле, где две точки на окружности образуют диаметр. На следующей неделе мы продолжим это доказательство для общего случая.

Решение логической головоломки

Переместите синюю монету над красной. На приведенной ниже схеме числа показывают количество монет в каждой стопке.

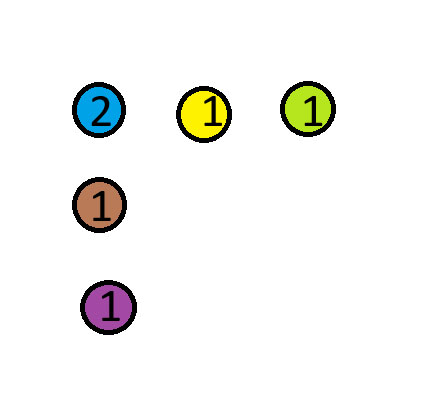
монеты

Благодарность: Эту головоломку я взял с YouTube-канала Mind Your Decisions . Это головоломка №3 в видео по ссылке.