Доказательство теоремы о вписанном угле (часть 2)

Возможно, вы помните, что на прошлой неделе я начал доказательство теоремы о вписанном угле. На этой неделе мы его завершим. Однако, прежде чем мы перейдем к этому, я, как обычно, представлю свою еженедельную логическую головоломку.

Логическая головоломка

Какие из следующих утверждений верны?

1. Одно из этих утверждений ложно.
2. Два из этих утверждений неверны.
3. Три из этих утверждений неверны.
4. Четыре из этих утверждений неверны.
5. Пять из этих утверждений неверны.
6. Шесть из этих утверждений неверны.
7. Семь из этих утверждений неверны.
8. Восемь из этих утверждений неверны.
9. Девять из этих утверждений неверны.
10. Десять из этих утверждений неверны.

Ответ находится в конце информационного бюллетеня.

Теорема о вписанном угле (часть 2)

Позвольте напомнить вам, что гласит теорема о вписанном угле.

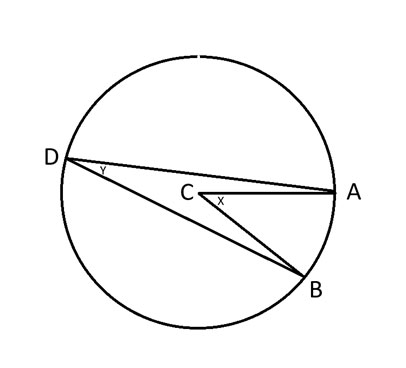
A, B и D = любые три точки на окружности.

C = Центр окружности.

x = Угол ACB.

y = Угол ADB.

Теорема о вписанном угле гласит, что угол 2y = x.

На прошлой неделе я показал, что это верно в конкретном случае, когда AD или BD образуют диаметр окружности. На этой неделе я использую это, чтобы показать, что теорема верна для общего случая для D.

Я собираюсь разбить все возможные места расположения точки D следующим образом:

Случай 1 = AD или BD образуют диаметр окружности (доказано на прошлой неделе)

Случай 2 = точка D лежит (или, может быть, «лежат»?) вдоль дуги на противоположной стороне окружности от точек A и B.

Случай 3 = Все остальные

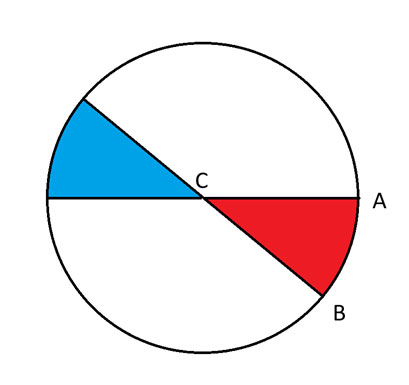
Другими словами, случай 2 будет охватывать случаи, когда точка D находится на краю круга в синей области. Случай 3 будет охватывать другие места за пределами этой синей области.

Для обсуждения воспользуемся следующей диаграммой.

Позволять:

x = x1 + x2

y = y1 + y2

z = z1 + z2

Мы стремимся доказать, что x = 2y

Я аккуратно провел линию от точки D до точки C, образующую диаметр окружности. Точка E — это точка пересечения этой линии с другой стороной окружности.

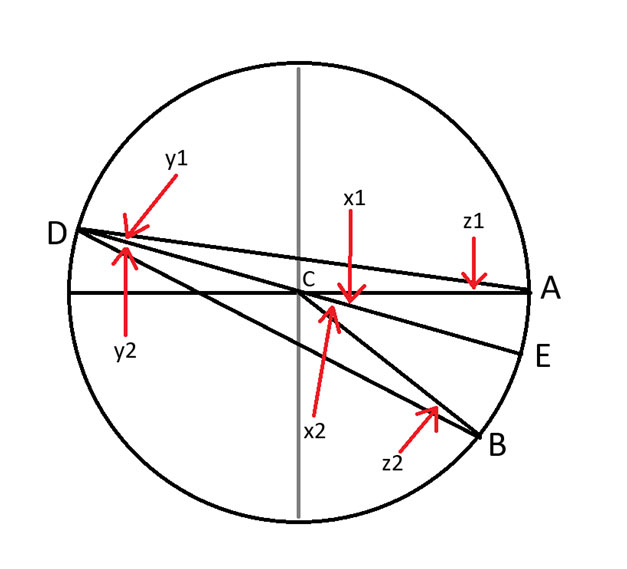
Числа в углах должны были быть указаны в нижнем индексе, но моя программа для рисования этого не позволила.

Рассмотрим треугольник ADE.

Поскольку DE образует диаметр, мы можем использовать то, что доказали на прошлой неделе, чтобы показать, что 2x1 = 2y1.

Теперь рассмотрим треугольник EDB.

По той же логике, _2x² = _y² .

Сложим эти уравнения:

2x ₁ + 2x ₂ = y ₁ + y ₂

2(x ₁ + x ₂ ) = y ₁ + y ₂

2x = y

На этом мы заканчиваем рассмотрение второго дела.

Рассмотрим случай 3.

Здесь мы попытаемся показать, что 2x ₁ = y ₁ .

Из случая 1:

_2x² = _y²

2(x ₁ + x ₂ ) = y< ₁ +y ₂

Вычитаем верхнее уравнение из нижнего:

2x ₁ = y ₁

И мы доказали правоту случая 3.

Ответ на логическую головоломку

Верно только утверждение 9.

Решение логической головоломки

У нас есть десять противоречащих друг другу утверждений. Если десять человек говорят разные вещи, то либо прав только один из них, либо никто из них не прав.

Рассмотрим случай, когда все десять утверждений ложны. В этом случае утверждение номер 10 будет истинным. Тогда ложными окажутся только девять утверждений. Таким образом, возникает противоречие. Должно существовать истинное утверждение. Но какое именно?

Если одно утверждение истинно, то девять ложны. Это утверждение номер 9 подтверждает. Следовательно, истинно только утверждение 9.