WOO logo

Wizard рекомендует

Большая математическая головоломка для видеозвонка Zoom


На прошлой неделе в моей рассылке был задан следующий вопрос. На всякий случай, вот сам вопрос.

Вопрос

Предположим, все 435 членов Палаты представителей США, имеющих право голоса, подключаются к одному и тому же видеозвонку в Zoom, запланированному на период с 9:00 до 10:00. Однако присутствие на всем звонке не обязательно, достаточно его части. Каждый участник случайным образом выбирает точный момент для подключения и выхода из звонка в пределах этого часового интервала.

Какова вероятность того, что хотя бы один представитель будет видеть лица всех остальных участников звонка одновременно? Другими словами, видеть лица всех остальных участников во время их участия в звонке, не обязательно всех одновременно.

Пожалуйста, прокрутите страницу вниз, чтобы увидеть мой ответ и решение.

Звонок через ZoomZoom-звонок - участники

Отвечать

2/3

Решение

Моя общая стратегия при решении вопросов, требующих ответа от большой группы людей, заключается в следующем: сначала отвечаю от двух человек. После того, как нахожу ответ, перехожу к трём. Затем, если вопрос не слишком сложный, перехожу к четвёртым. Если вижу закономерность, велика вероятность, что эта закономерность будет применима к любому количеству людей.

Обзор основ математики

Прежде чем продолжить, я буду часто использовать функцию combin(x,y). Это количество способов выбрать y предметов из группы из x. Например, количество способов выбрать пять карт из 52, где порядок не имеет значения, равно combin(52,5) = 2 598 960. Ответ можно выразить как x! / (y! * (xy)!).

В данном случае восклицательный знак не означает, что я кричу, а обозначает факториал. Это количество способов упорядочить любое заданное количество предметов. Например, если вам нужно прочитать шесть книг по одной, количество возможных порядков книг равно 6!. Ответ для общего случая n — 1*2*3*…*n. В случае шести книг ответ — 1*2*3*4*5*6 = 720.

Дело двух человек

Итак, давайте решим задачу для случая с двумя участниками. Точное время начала и окончания звонка не имеет значения, важна только последовательность событий. Давайте используем букву для обозначения конкретного участника, входящего/выходящего из звонка. Начиная слева, первое использование данной буквы будет обозначать вхождение в звонок, а второе — выход из него.

6;font-family: 'Open Sans',sans-serif;color: #313131!important">Из четырех мест в истории вызовов существует 6 комбинаций, позволяющих разместить букву А:

1. AABB

2. ABAB

3. ABBA

4. БААБ

5. БАБА

6. BBAA

Давайте проверим, были ли оба абонента подключены одновременно в каждом из сценариев:

1. AABB - Нет, А пришел и ушел до того, как Б присоединился к разговору.

2. ABAB - Да, было совпадение между прибытием B и отъездом A.

3. ABBA - Да, было совпадение между прибытием и отъездом B.

4. BAAB - Да, было совпадение между прибытием А и отъездом А.

5. БАБА - Да, было совпадение между прибытием А и отъездом В.

6. BBAA - Нет, Б пришел и ушел до того, как А присоединился к разговору.

Каждый сценарий одинаково вероятен. Четыре из шести сценариев частично совпадали, поэтому вероятность совпадения в случае с двумя людьми составляет 2/3.

Дело с участием трех человек

В случае с тремя участниками количество историй звонков равно произведению количества способов, которыми человек А может выбрать два места из 6 в истории, и количества способов, которыми человек В может выбрать 2 из 4 оставшихся мест. Это равно combin(6,2)*combin(4,2) = 15*6 = 90.

Перечислять все 90 было бы утомительно. Давайте упростим ситуацию, предположив, что человек А присоединяется первым. Кто-то же должен быть первым, так что это вполне может быть А.

Для начала рассмотрим ситуацию, когда следующим событием в истории звонков является уход А. Обозначим это как AA????. Независимо от того, как B и C войдут и выйдут из звонка, никто не пересечёт A. Таким образом, вероятность успеха сценария AA равна 0. Вероятность самого сценария AA равна 1/5, потому что после того, как А занял первое место, было пять возможных событий: A, B, B, C и C.

Во-вторых, рассмотрим ситуацию, когда А присоединяется первым, затем В, а потом А уходит. В этом случае В представляет любого человека, кроме А (который уже завершил звонок). Это обозначается как ABA???. Оставшиеся буквы для размещения — B, C и C. Из трех способов размещения B (BCC, CBC и CCB) варианты CBC и CCB приводят к тому, что B перекрывает как A, так и C.Таким образом, вероятность успеха в сценарии ABA составляет 2/3. Вероятность самого сценария равна pr(кто-либо, кроме А, присоединяется) * pr(А покидает) = (4/5) * (1/4) = 1/5, где pr(x) представляет вероятность события x.

В-третьих, рассмотрим ситуацию, когда А присоединяется первым, затем В, а потом В уходит. Это обозначается как ABB???. Оставшиеся буквы для размещения — А, С и С. Из трех способов размещения А (ACC, CAC и CCA) варианты CAC и CCA приводят к тому, что А перекрывает как В, так и С. Таким образом, вероятность успеха в сценарии ABB составляет 2/3. Вероятность самого сценария равна pr(кто-либо, кроме А)*pr(В уходит) = (4/5)*(1/4) = 1/5.

В-четвертых, рассмотрим ситуацию, когда первым присоединяется А, затем В, а потом С. Это обозначается как ABC??? Оставшиеся буквы, которые нужно разместить, — А, В и С. Легко заметить, что где бы А ни покинул звонок, он перекроет В и С. Таким образом, вероятность успеха в этом сценарии равна 1. Вероятность самого сценария равна pr(присоединение любого, кроме А) * pr(присоединение третьего лица) = (4/5) * (2/4) = 2/5.

Мы рассмотрели все возможные сценарии, о чем свидетельствует сумма вероятностей (1/5 + 1/5 + 1/5 + 2/5), равная 1. Взяв скалярное произведение вероятности каждого сценария и вероятности его успеха, получаем: (1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3.

Дело четырех человек

Если бы у меня было мало времени, я бы, наверное, предположил, что ответ на исходный вопрос — 2/3, поскольку это справедливо для случаев с двумя и тремя людьми. Однако это кажется слишком неудовлетворительным, поэтому давайте перейдем к случаю с четырьмя людьми.Я могу разбить это на десять возможных сценариев, а именно:

  1. АА??????

    Вероятность сценария = 1/7

    Вероятность успеха = 0 (никто не может перекрывать точку А)

  2. АБА???

    Вероятность сценария = 1/7

    Вероятность успеха = 16/30

  3. ABBA???

    Вероятность сценария = 1/35

    Вероятность успеха = 0 (никто не может перекрываться с точкой B)

  4. ABBC???

    Вероятность сценария = 4/35

    Вероятность успеха = 2/3

  5. ABCA???

    Вероятность сценария = 4/35

    Вероятность успеха = 5/6

  6. ABCBA???

    Вероятность сценария = 1/35

    Вероятность успеха = 2/3

  7. ABCBC???

    Вероятность сценария = 1/35

    Вероятность успеха = 2/3

  8. ABCBD???

    Вероятность сценария = 2/35

    Вероятность успеха = 1 (A будет пересекаться с B, C и D)

  9. ABCC???

    Вероятность сценария = 4/35

    Вероятность успеха = 5/6

  10. ABCD???

    Вероятность сценария = 8/35

    Вероятность успеха = 1 (A будет пересекаться с B, C и D)

Приношу извинения за то, что не стал подробно разбираться в математических расчетах для каждой ситуации, но я не хотел, чтобы это решение занимало слишком много времени, и хотел оставить часть работы читателю.

В следующей таблице приведено краткое описание всех десяти сценариев дела с участием четырех человек.

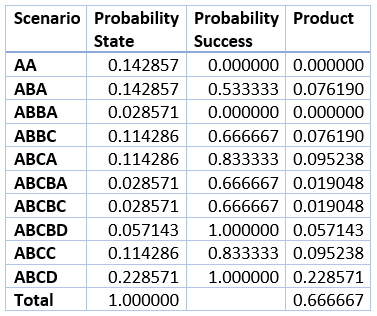
Кейс с участием четырех человек - десять сценариев

В нижней правой ячейке таблицы указана вероятность 2/3.

Краткое содержание

Мы показали вероятность 2/3 для случаев с двумя, тремя и четырьмя людьми. Логично предположить, что эта вероятность, вероятно, сохранится для любого количества людей. Моделирование и математические расчеты, проведенные более умными людьми, чем я, подтвердили это.

Ссылки

Данная задача была переформулирована по сравнению с вопросом, заданным в рубрике Riddler Classic на сайте FiveThirtyEight. Ссылка

Обсуждение этой проблемы на моём форуме. Ссылка.

Автор: Michael Shackleford