Как применять правило PEMDAS.

Если вы похожи на меня, то в вашей ленте прямых эфиров на Facebook вам постоянно задают вопросы о порядке выполнения операций. За каждым из них следуют сотни ответов в комментариях, в которых большинство людей ошибаются. Число людей, которые когда-либо признают свою ошибку, неизменно равно нулю.

Что делает мое мнение верным? Во-первых, если позволите, я хотел бы считать себя признанным ведущим специалистом в области математики азартных игр. Поищите любую азартную игру или термин, и вы увидите мое имя повсюду. Кроме того, у меня есть степень по математике и экономике Калифорнийского университета в Санта-Барбаре, и я являюсь членом Общества актуариев в отставке. Все, чем я занимался после окончания университета, так или иначе было связано с математикой.

Примером такого вопроса может служить:

6 ÷ 2 (1 + 2) = ?

Остановитесь на мгновение и подумайте.

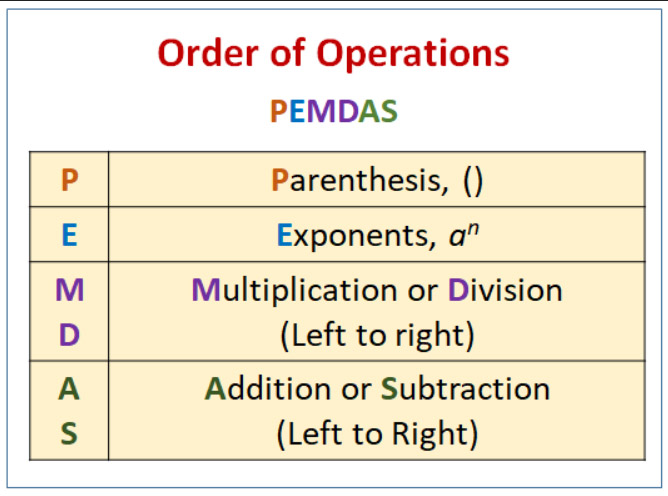
Если вы ответили 1, то вы ошиблись. Я подозреваю, что вы ошиблись, потому что используете эмпирическое правило PEMDAS для порядка выполнения операций. Это мнемоническое правило преподают примерно в 5 классе. Мне его объясняли так: «Пожалуйста, извините мою дорогую тетю Салли». Оно призвано научить детей оценивать выражения в следующем порядке:

1. 1. Скобки
2. 2. Показатели степени
3. 3. Умножение
4. 4. Раздел
5. 5. Арифметика
6. 6. Вычитание

Вероятно, ваш учитель в начальной школе действительно считал это правильным. Однако это не так. Я не знаю, откуда это взялось, но подозреваю, что это упрощенный способ запоминания, который легко понимают десятилетние дети. Проблема упрощения чего-либо заключается в том, что, хотя в большинстве случаев это может привести к правильному ответу, часто бывают исключения из правила.В случае с PEMDAS это привело бы к решению задачи 6 ÷ 2 (1 + 2), сформулированной ранее следующим образом:

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) , потому что сначала нужно вычислить скобки.
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 , потому что ни один оператор вне скобок не подразумевает умножение.
3. 6 ÷ 2 × 3 = 6 ÷ 6 , потому что умножение выполняется перед делением, согласно PEMDAS.
4. 6 ÷ 6 = 1

Ошибка в приведенной выше логике заключается в третьем шаге. Умножение не всегда предшествует делению. Они имеют одинаковый приоритет. Если оба действия встречаются в одном выражении, сначала следует выполнить то, которое находится левее.

Добавлю, что сложение не обязательно должно предшествовать вычитанию. Они также имеют равный приоритет. Однако в случае сложения и вычитания, где не применяются более высокие правила, не имеет значения, что вы делаете первым.

Вот правильный способ вычисления 6 ÷ 2 (1 + 2):

1. 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) , потому что сначала нужно вычислить скобки.
2. 6 ÷ 2 (3) = 6 ÷ 2 × 3 , потому что ни один оператор вне скобок не подразумевает умножение.
3. 6 ÷ 2 × 3 = 3 × 3 , потому что и при умножении, и при делении сначала вычисляют значение слева.
4. 3 × 3 = 9

Вот ещё один вопрос к вам:

7 + 7 ÷ 7 + 7 × 7 – 7 = ?

На Facebook можно увидеть ответ 56. В этом случае люди ошибаются не из-за правил PEMDAS, а потому что «мой калькулятор показал ответ 56». Это ленивый и неверный ответ, который дают те, кто просто ходит слева направо.Неверное рассуждение таково:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7 , потому что сначала вычисляют слева.
2. 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7 , потому что сначала вычисляют слева.
3. 2 + 7 × 7 – 7 = 9 × 7 – 7 , потому что сначала вычисляют слева.
4. 9 × 7 – 7 = 63 – 7 , потому что сначала вычисляют слева.
5. 63 – 7 = 56

Правильный способ оценки этого задания:

1. 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 , потому что деление предшествует сложению и находится слева от умножения.
2. 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 , потому что умножение превосходит сложение и вычитание.
3. 7 + 1 + 49 – 7 = 8 + 49 – 7 , потому что между сложением и вычитанием сначала выполняется операция слева.
4. 8 + 49 – 7 = 57 – 7 , потому что между сложением и вычитанием сначала выполняйте операцию слева.
5. 57 – 7 = 50

Обратите внимание, что в этом вопросе PEMDAS всё правильно. Люди ошибаются, неправильно используя калькуляторы. Крайне важно вводить числа и операции в правильном порядке. Это гораздо проще сделать с калькуляторами, использующими обратную польскую запись, например, HP15C. Кстати, любой, у кого есть HP15C или 12C, сразу становится моим другом.

В заключение я хотел бы добавить свою изюминку в эти головоломки, связанные с порядком действий, — это головоломка, которую я создал сам, как с точки зрения логики, так и с точки зрения расположения элементов. Признаюсь, я позаимствовал изображения из Google. Эта головоломка была вдохновлена похожей, но ещё более сложной, головоломкой с YouTube-канала Mind Your Decisions . Пожалуйста, разместите её где угодно; я надеюсь, она станет вирусной.

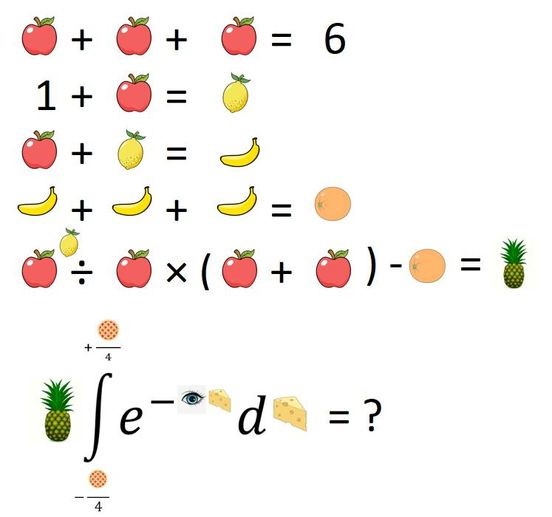
Частичные баллы начисляются за решение уравнения только для ананаса, полные баллы — за решение интеграла.

Ответы я опубликую в информационном бюллетене от 29 июня. А до тех пор пусть удача будет на вашей стороне.

Автор: Michael Shackleford