Участники шоу «Цена правильная» выстраиваются в ряд

Прежде чем перейти к основной теме, небольшое обновление. На прошлой неделе я писал о процессе покупки билетов на Burning Man. В среду я решил рискнуть и купить билеты в основной распродаже. Как вы помните, последним препятствием было быть готовым купить билеты ровно в полдень 30 марта. Я был готов. На самом деле, у меня было три браузера со ссылкой на распродажу. Честно говоря, я не уверен, что это повысило мои шансы, но другие источники о Burning Man рекомендуют так делать.

Короче говоря, билета я не получил. Этого следовало ожидать. По крайней мере, я попытался. В отличие от 2019 года, изображение на моих экранах, которое вы видите ниже, обновилось примерно через полчаса после начала продажи билетов, когда выяснилось, что они распроданы. Вы можете спросить, нажал ли я кнопку «назад», хотя на экране написано, что это не поможет. Я этого не сделал.

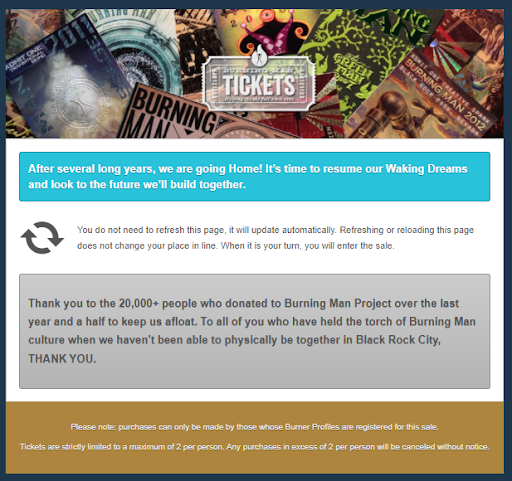
Похоже, в этом году я не поеду на Burning Man. Ничего страшного. У меня есть ещё немало других идей для отпуска.

Переходим к главной теме, а именно к игре «Ряд участников» в программе «Цена правильная». Эта игра проводится шесть раз в каждом выпуске. Для тех, кто еще не знает, вот правила:

1. Для участия в следующей игре на определение цены выбираются четыре игрока.
2. Показан предмет, стоимость которого обычно составляет от 1000 до 2000 долларов. Например, хороший велосипед.
3. Игроки в указанном порядке будут делать ставки на стоимость предмета.
4. Игрок, чья ставка окажется наиболее близкой к фактической стоимости, но не превысит её, выигрывает товар и получает право участвовать в следующей игре по определению цены.
5. Если все четыре игрока перебили ставку, то они делают повторные ставки в том же порядке, получая указание не превышать самую низкую ставку предыдущего раунда. Это будет продолжаться до тех пор, пока в одном из раундов хотя бы один игрок не перебьет ставку.

Какова должна быть ваша стратегия в этой игре, если вы ничего не знаете о стоимости приза?

Большинство участников шоу имеют ужасную стратегию. Допустим, вы делаете последнюю ставку, а предыдущие ставки составляли 1500, 1600 и 2400 долларов. Лучшие ставки, опять же, не зная ничего о стоимости предмета, будут следующими:

• 1 доллар: Это охватывает диапазон в 1499 долларов — суммы от 1 до 1499 долларов, хотя призы никогда не приближаются к 1 доллару.
• 1601 доллар: Эта сумма охватывает диапазон от 1600 до 2399 долларов (приблизительно 800 долларов).
• 2401 доллар: Этот диапазон значений бесконечен – от 2400 долларов до бесконечности.

Вы постоянно видите, как игроки делают ставки, которые неоправданно уступают диапазону. В приведенном выше примере это 2000 долларов. Это означает, что диапазон от 1600 до 1999 долларов будет потерян по сравнению со ставкой в 1600 долларов, и все это бесплатно.

Не существует универсального правила, подходящего для всех ситуаций. Просто постарайтесь охватить как можно более широкий диапазон, особенно в том диапазоне, куда обычно попадают призы.

А что, если бы в игре участвовали четыре логика, спросите вы? Давайте предположим, что логики ничего не знают о стоимости приза. Для упрощения объяснений предположим, что участники могут делать ставки до копейки.

6;font-family: 'Open Sans',sans-serif;color: #313131!important">Давайте начнем с простой ситуации, где стоимость приза случайна и выбирается из равномерного распределения от 0 до 1000 долларов. Очевидно, что у последнего хода есть позиционное преимущество. Я не буду вдаваться в математику, но вот как должны делать ставки четыре логика, в порядке от первого к последнему:

• Игрок 1: 777,80 долларов США
• Игрок 2: 555,57 долларов США
• Игрок 3: 333,33 доллара
• Игрок 4: 0,01 $, 333,34 $, 555,57 $ или 777,79 $.

Ключевой момент заключается в том, что первые три игрока стремятся довести всех последующих игроков практически до точки безразличия. Каждый из них хочет максимально ограничить пространство, не побуждая при этом следующего игрока делать ставки на 0,01 доллара выше своих.

Если они будут делать ставки таким образом, у игрока 4 будет 33,3% шансов на победу, независимо от четырех возможных ставок, которые я для него указал. У каждого из остальных игроков будет 22,2% шансов на победу. Я добавил одну или две копейки к ставкам игроков 1 и 2, чтобы игроки 3 и 4 не перебили их на 0,01 доллара.

Однако это нереалистичный пример, поскольку стоимость призов, как правило, подчиняется экспоненциальному распределению. Чтобы сделать его более реалистичным, предположим, что стоимость приза выбирается случайным образом из экспоненциального распределения со средним значением 1000 долларов.

Не вдаваясь в математические расчеты, вот оптимальные ставки при вышеуказанном предположении:

• Игрок 1: 1504,08 долларов США
• Игрок 2: 810,98 долларов США
• Игрок 3: 405,47 долларов
• Игрок 4: 0,01 $, 405,48 $, 810,99 $ или 1504,09 $

Вероятность выигрыша будет такой же, как и в первом случае: 33,3% для игрока 4 и 22,22% для всех остальных.

На этом всё на этой неделе. До новых встреч, пусть удача будет на вашей стороне.

Автор: Michael Shackleford