Доказательство формулы Пифагора

На этой неделе я докажу классическую формулу Пифагора, которая гласит, что в прямоугольном треугольнике сумма квадратов сторон равна квадрату гипотенузы. Самый известный пример — прямоугольный треугольник со сторонами 3, 4 и 5. Заметьте, ^3² + ^4² = ^5² . Однако, прежде чем мы перейдем к этому, я представлю обычную еженедельную логическую головоломку.

Логическая головоломка

Рассеянный античный философ забыл завести свои большие настенные часы в доме. У него не было ни радио, ни телевизора, ни телефона, ни интернета, ни каких-либо других средств для определения времени. Поэтому он пешком отправился к другу, который жил в нескольких милях от него по прямой пустынной дороге. Он переночевал у друга, а когда вернулся домой, уже знал, как завести часы. Откуда он это знал?

Ответ находится в конце информационного бюллетеня.

Доказательство формулы Пифагора

Рассмотрим следующую диаграмму, которая состоит из большого квадрата, разделенного на четыре равных прямоугольных треугольника, и меньшего квадрата посередине. Посередине будет квадрат, потому что сумма углов любого треугольника равна 180 градусам. Я доказал это в информационном бюллетене от 13 ноября 2025 года .

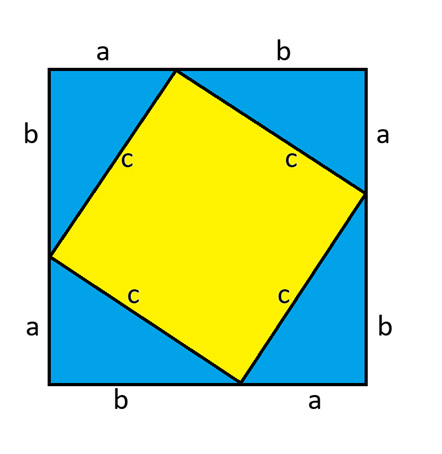
Площадь большого квадрата равна (a+b) ^² . Площадь каждого треугольника равна ab² . Площадь жёлтого квадрата посередине равна ^c² . Приравнивая площадь большого квадрата к сумме его внутренних частей, получаем:

6; font-family: 'Open Sans', sans-serif; color: #313131 !important;">(a+b) ² = 4 ab 2 + c ²

^a² + 2ab + ^b² = 2ab + ^c²

Вычтем 2ab из обеих сторон, получим:

^a² + ^b² = ^c²

Решение логической головоломки

1. Профессор завел часы и установил произвольное время.
2. Придя к дому друга, он записал время прибытия.
3. Уходя, он отмечает время своего ухода, а также подсчитывает время, проведенное в доме друга, вычитая время своего прибытия из времени ухода.
4. Он старается идти обратно с той же скоростью, что и до дома друга.
5. Когда он вернется домой, на его часах отобразится время, проведенное в доме друга, плюс время, потраченное на пешую прогулку. Время на пешую прогулку он может рассчитать, вычитая время, проведенное в доме друга, из общего времени. Затем он может рассчитать время в одну сторону, разделив общее время на пешую прогулку на 2.
6. Затем он может установить на своих часах время, когда он вышел из дома друга, плюс время, затраченное на пешую прогулку в одну сторону.

Рассмотрим пример.

Неправильно заведенные часы установлены на 12:00. В 8:00 он прибывает к другу. В 1:00 он уходит, отмечая, что визит длился пять часов. Вернувшись, он видит, что его часы показывают 8:00. Вычитая пятичасовой визит, это означает, что он потратил в общей сложности три часа на ходьбу. То есть 1,5 часа в одну сторону. Если он вышел в 1:00 и шел 1,5 часа, то сейчас должно быть 2:30, на которое он затем устанавливает свои часы.